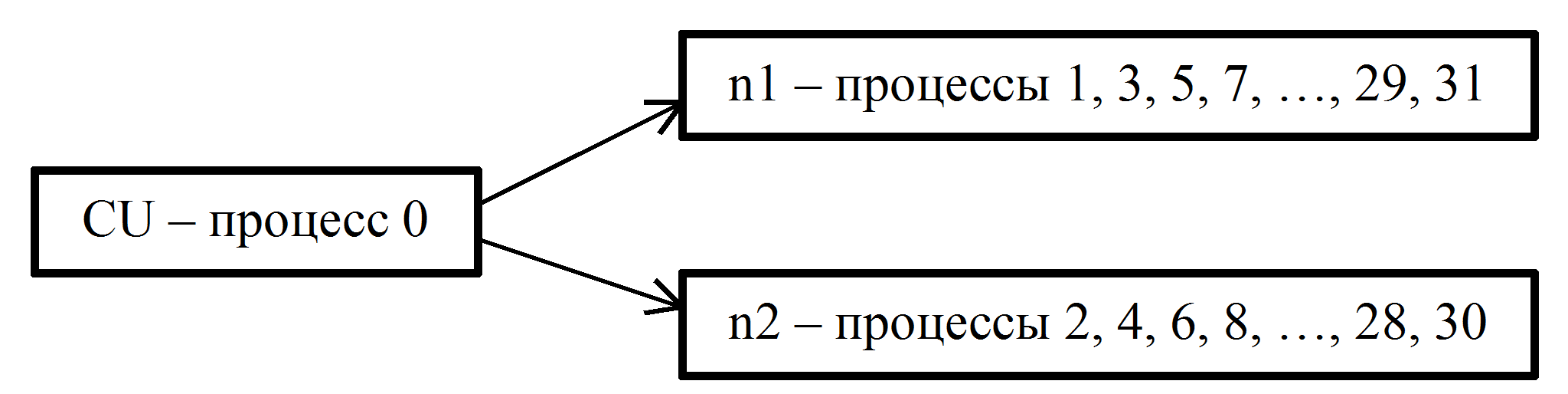- Для решения прикладных и научных задач, требующих
больших вычислительных мощностей, широко применяются кластерные
вычислительные системы [1 - 5]. Одной из таких задач является расчет
параметров наноматериалов [6 - 9]. В [8] рассматриваются
вопросы вычисления коэффициентов матрицы, необходимой для дальнейших
расчетов, на кластере СКИФ МГУ «Чебышёв».
В настоящее время во многих ВУЗах Российской Федерации имеются
кластеры с небольшим количеством процессорных ядер
(мини-кластеры) [10].
В предлагаемой работе рассматриваются вопросы вычисления
матриц на мини-кластере.
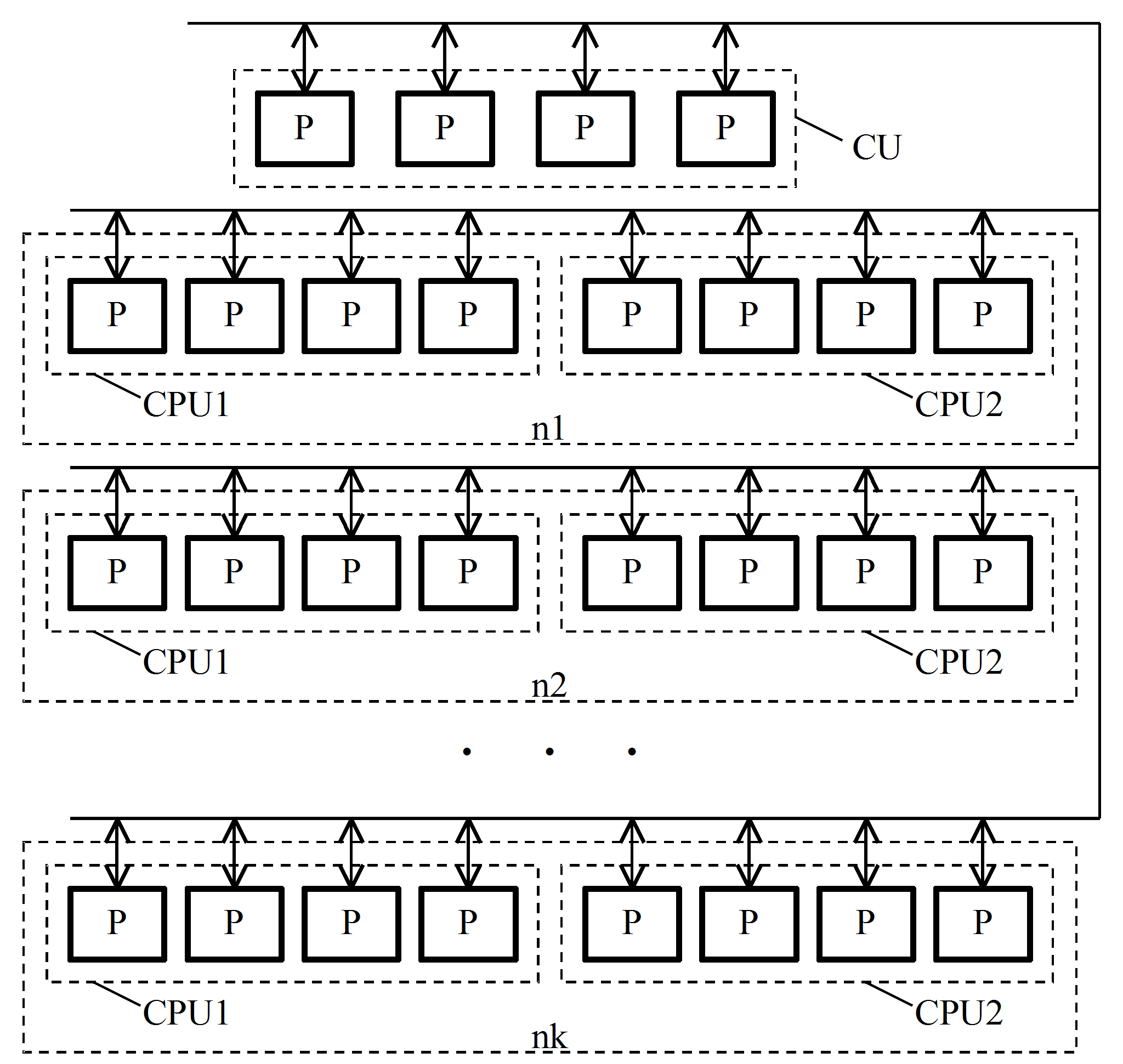
- Типовая структура мини-кластера приведена на рис. 1.
Рис. 1. Структура мини-кластера.
-
Кластер содержит управляющий узел
CU
и несколько вычислительных узлов n1, n2, . . . nk.
Управляющий узел CU
реализуется на многоядерном процессоре и содержит несколько
процессорных ядер P.
Каждый вычислительный узел обычно содержит два многоядерных
процессора CPU1
и CPU2,
каждый из которых имеет несколько ядер P.
Все узлы соединяются в единую сеть, для обмена используются
протоколы Ethernet,
Infiniband, Myrinet
и другие. При решении задач может применяться GNU C
в сочетании с системой Linux.
При запуске программы с использованием системы MPI
нулевой поток запускается на процессоре управляющего узла CU,
а остальные потоки равномерно распределяются по процессорным ядрам
узлов n1, n2, . . . nk.
- Как известно, современные компьютеры, обладают достаточно сложной архитектурой. Учесть теоретически все их особенности весьма затруднительно, поэтому построить их теоретическую модель весьма проблематично. Особенно сложной архитектурой обладают суперкомпьютерные системы, в том числе кластеры. Поэтому, для их исследования в настоящем разделе был выбран экспериментальный метод. В литературе для сравнения быстродействия различных компьютеров используют тестовые задачи [1]. Однако в данном разделе решается конкретная задача: обеспечение вычисления матриц на мини-кластере за приемлемое время, поэтому исследование проводилось на рабочей программе. В рассматриваемом случае требуется вычислять элементы матрицы для куба размером m3, где m – количество интервалов по каждой координате [6 - 8]. Основная часть программы представляет собой множество вложенных циклов, в которых вычисляется многомерный массив переменных [6, 7]. Эти переменные вычисляются по формуле, которая в упрощенном виде выглядит следующим образом:
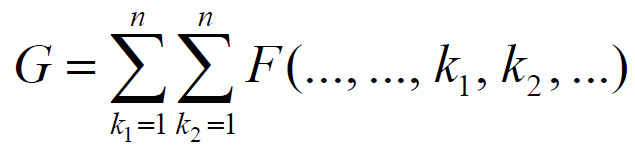 ,
,- где
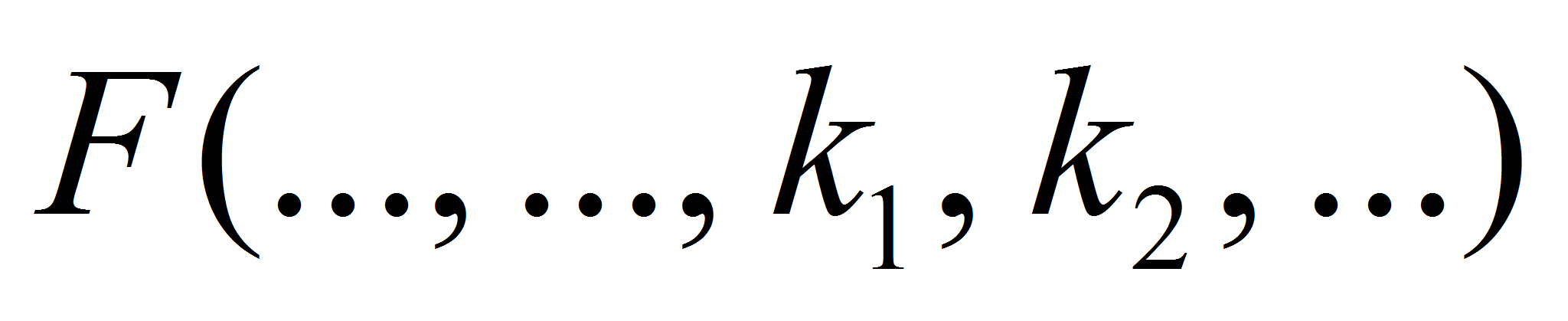 -
функция от ряда переменных, в том числе от
-
функция от ряда переменных, в том числе от
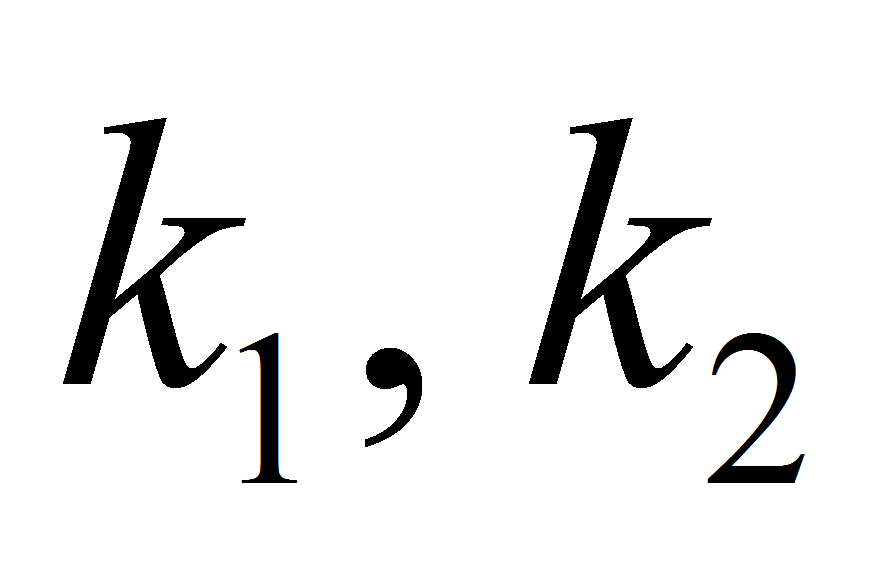 .
Таким образом, время решения существенно зависит от m и n.
.
Таким образом, время решения существенно зависит от m и n.- Были выполнены ряд решений при различных значениях m и n. Переменная m задает количество повторений во внешних циклах, а также существенно влияет на величину матрицы. Переменная n влияет в основном на объем вычислений, она задает количество повторений во внутренних циклах [6 - 8].
- Если вычисления производить на обычном компьютере, то организация трех внешних циклов будет следующей:
for (i1 = 0; i1 < m; i1++){
- for (i2 = 0; i2 < m; i2++){
- for (i3 = 0; i3 < m; i3++){
- // внутренние циклы
- }
- }
- }
- При использовании кластера вычисления распределяются по отдельным процессам При небольшом числе процессорных ядер nc в кластере (nc ≤ m2) для распределения можно использовать только переменные i1 и i2. Наиболее простым представляется случай, когда m2 кратно np (np - число процессов). Кроме того, целесообразно, чтобы m было кратно m2/np. Так, например, при m=6 можно использовать np=6, 12, 18 и 36; при m=8 можно использовать np=8, 16, 32 и 64. В этом случае распределение по процессам двух внешних циклов будет наиболее простым, третий цикл просчитывается полностью во всех процессах.
- Для процесса с номером me переменная i1 определяется оператором
i1=(int)(me/(np/m));
- а i2 принимает значения от i2c до i2c+i2b, при этом i2b и i2c вычисляются операторами: i2b=(m*m)/np; i2c=i2b*(me%(np/m)).
- Организация циклов в каждом процессе будет следующей:
- for (i2 = i2c; i2 < i2c+i2b; i2++){
- for (i3 = 0; i3 < m; i3++){
- // внутренние циклы
- }
- }
- Для сбора данных используется функция MPI_Gather.
- Были выполнены решения для разных np и n при m=8, количество используемых процессорных ядер в вычислительных узлах - 16. Результаты решения приведены в таблице 1 (эти данные получены при уровне оптимизации O3). Анализ результатов показывает, что при n≥50 и np≥nc время вычисления изменяется мало. Имееется некоторое увеличение времени решения при увеличении np для n=15, однако этот результат не представляет интереса для практики. Даже если этот случай будет необходим, то время решения невелико, и то увеличение времени, которое наблюдалось, в абсолютном значении также невелико.
- Как известно, современные компьютеры, обладают достаточно сложной архитектурой. Учесть теоретически все их особенности весьма затруднительно, поэтому построить их теоретическую модель весьма проблематично. Особенно сложной архитектурой обладают суперкомпьютерные системы, в том числе кластеры. Поэтому, для их исследования в настоящем разделе был выбран экспериментальный метод. В литературе для сравнения быстродействия различных компьютеров используют тестовые задачи [1]. Однако в данном разделе решается конкретная задача: обеспечение вычисления матриц на мини-кластере за приемлемое время, поэтому исследование проводилось на рабочей программе. В рассматриваемом случае требуется вычислять элементы матрицы для куба размером m3, где m – количество интервалов по каждой координате [6 - 8]. Основная часть программы представляет собой множество вложенных циклов, в которых вычисляется многомерный массив переменных [6, 7]. Эти переменные вычисляются по формуле, которая в упрощенном виде выглядит следующим образом:
Таблица 1
Время решения (сек) для разных np и n при m=8
|
np |
8 |
16 |
32 |
64 |
|
n=15 |
63 |
34 |
37 |
43 |
|
n=50 |
529 |
255 |
266 |
269 |
|
n=100 |
2126 |
1085 |
1072 |
1062 |
|
n=200 |
8516 |
4383 |
4287 |
4269 |
|
n=500 |
54405 |
28847 |
27994 |
28014 |
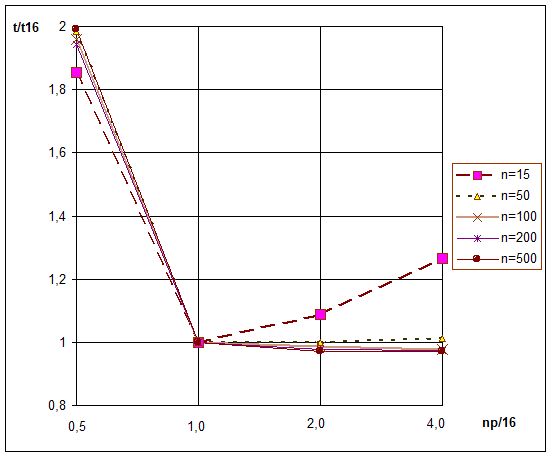
- По результатам, приведенным в таблице 1, были построены графики на рис. 2.
- На этом рисунке по горизонтальной оси приведены относительные значения np/nc – среднее число процессов на каждое процессорное ядро. По вертикальной оси приведено относительное время t/t16, где t – время решения, t16 – время решения при np=16. Увеличение времени при np<16 прогнозируемо и практически совпадает с ожидаемым значением, в этом случае используются не все процессорные ядра. При увеличении np, в частности при np=64, когда на каждое процессорное ядро приходится в среднем около четырех процессов, можно было бы ожидать некоторого увеличения времени решения вследствие того, что при увеличении количества процессов должно увеличиваться время переключения между процессами. Однако, очевидно, влияние этого фактора мало. Более того, наблюдается даже некоторое уменьшение времени решения. Возможная причина этого уменьшения заключается в следующем.
- По результатам, приведенным в таблице 1, были построены графики на рис. 2.
Рис 2. Время решения для разных np и n при m=8
-
- Во время эксперимента использовались два вычислительных узла, каждый из которых содержит два процессора, в каждом из которых в свою очередь имеется четыре процессорных ядра. В соответствии с правилами MPICH процессы распределяются по узлам следующим образом. Нулевой процесс запускается на управляющем узле, а остальные процессы последовательно распределяются по вычислительным узлам. Для упрощения будем считать, что каждый узел имеет по 8 равноправных процессорных ядер, а деление на процессоры отсутствует.
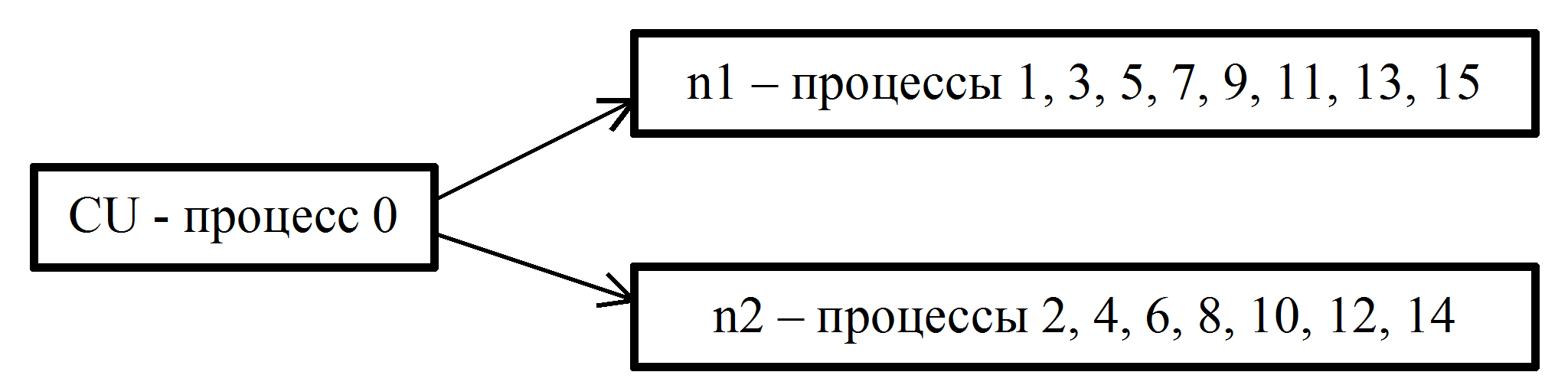
- Пусть np=16. В этом случае распределение процессов по узлам n1 и n2 будет следующим (см. рис. 3)
- Во время эксперимента использовались два вычислительных узла, каждый из которых содержит два процессора, в каждом из которых в свою очередь имеется четыре процессорных ядра. В соответствии с правилами MPICH процессы распределяются по узлам следующим образом. Нулевой процесс запускается на управляющем узле, а остальные процессы последовательно распределяются по вычислительным узлам. Для упрощения будем считать, что каждый узел имеет по 8 равноправных процессорных ядер, а деление на процессоры отсутствует.
Рис. 3. Распределение процессов по вычислительным узлам
-
- В управляющем узле CU выполняется 0-й процесс, в вычислительном узле n1 выполняются процессы с нечетными номерами, в n2 - с четными номерами. При этом в узле n1 выполняются 8 процессов, узле n2 - 7 процессов. Таким образом, можно считать, что в узле n2 практически не используется одно из процессорных ядер, что немного снижает быстродействие.
- Пусть np=32. В этом случае распределение процессов по узлам n1 и n2 будет следующим (см. рис. 4)
- В управляющем узле CU выполняется 0-й процесс, в вычислительном узле n1 выполняются процессы с нечетными номерами, в n2 - с четными номерами. При этом в узле n1 выполняются 8 процессов, узле n2 - 7 процессов. Таким образом, можно считать, что в узле n2 практически не используется одно из процессорных ядер, что немного снижает быстродействие.
Рис. 4. Распределение процессов по вычислительным узлам для np=32.
-
- В управляющем узле CU выполняется 0-й процесс, в вычислительном узле n1 выполняются процессы с нечетными номерами, в n2 - с четными номерами. При этом в узле n1 выполняются 16 процессов, в узле n2 - 15 процессов. В этом случае оба узла загружаются полностью. (При этом следует отметить, что узел n2 завершает работу немного раньше узла n1). Аналогичные исследования были проведены для других m. Анализ результатов показывает, что при n≥200 и np>nc время решения изменяется мало, что в целом согласуется с результатами для m=8, приведенными в таблице 1.
- Приведенные в таблице 1 результаты показывают, что время решения n ≥ 200 составляет несколько часов. При увеличении m и n время решения может составлять несколько суток, поэтому актуальным является решение вопросов, связанных с сокращением времени решения. Для повышения скорости программ рекомендуется использовать различные методы [11 – 13], однако, у разных авторов иногда есть противоположные точки зрения на отдельные стороны совершенствования программ. В то же время практически все авторы основным методом повышения скорости работы программ, с которого надо начинать, считают нахождение так называемых «узких» мест. В программе вычисления матриц таким «узким» местом являются участки, содержащие два вложенных цикла по n. В [11 – 13] утверждается, что «узкие» места обычно занимают небольшую часть программы (единицы процентов) и улучшение этих участков может дать существенный выигрыш в быстродействии. Кроме того, авторы этих книг утверждают, что оптимизация остальных частей дает незначительный прирост быстродействия и является неэффективной (излишней). В соответствии с этими рекомендациями было проведено улучшение только указанных «узких» мест, остальная часть программы не затрагивалась.
- Для программы вычисления матриц характерно использование комплексных чисел с двойной точностью. Каждое такое число занимает в памяти 16 байт. При вызове функций приходится передавать в вызываемую функцию определенную порцию чисел. В результате при вызове функций передается значительное количество данных, что приводит к тому, что «узким» местом становятся вызовы функций. В связи с этим было проведено исследование влияние исключений вызовов функций в наиболее интенсивно работающих участках. Содержимое функций переносилось в основную программу, в результате чего увеличивался размер программы. В различных средах программирования (Visual C, GNU C и других) имеются режимы (опции), задающие автоматическое встраивание функций в вызывающую программу, но эти режимы работают только для простых функций и эффективны далеко не всегда. Попытки их использования в исследуемых программах не дали существенного результата. Поэтому встраивание функций в вызывающую программу в настоящей работе производилось вручную. Экспериментальное исследование рабочей программы производилось в системе Linux с применением средств GNU C++, которые использовались в исследуемом кластере. Сравнивались два варианта программ, первоначальный, в котором имеется множество вызовов функций, и модифицированный вариант, в котором в наиболее часто повторяющихся участках функции встроены в вызывающую программу. Решение выполнялось на мини-кластере с использованием 16 процессорных ядер при уровне оптимизации O0. В результате исследования были получены следующие результаты (см. таблицу 2).
- В управляющем узле CU выполняется 0-й процесс, в вычислительном узле n1 выполняются процессы с нечетными номерами, в n2 - с четными номерами. При этом в узле n1 выполняются 16 процессов, в узле n2 - 15 процессов. В этом случае оба узла загружаются полностью. (При этом следует отметить, что узел n2 завершает работу немного раньше узла n1). Аналогичные исследования были проведены для других m. Анализ результатов показывает, что при n≥200 и np>nc время решения изменяется мало, что в целом согласуется с результатами для m=8, приведенными в таблице 1.
Таблица 2
Время решения программы при различных способах вычисления функций.
|
n |
50 |
100 |
200 |
500 |
1000 |
|
t с |
1657 |
6665 |
26850 |
171161 |
684346 |
|
tm с |
425 |
1701 |
6876 |
44323 |
178076 |
|
t / tm |
3.90 |
3.92 |
3.90 |
3.86 |
3.84 |
- В верхней строке указаны значения n, задающие число повторений и соответственно время решения программы. Во второй строке указывается время t решения первоначального (немодифицированного) варианта программы в секундах. В третьей строке указано время tm решения модифицированного варианта программы в секундах (в этом варианте содержимое функций вручную встроено в вызывающую программу). В последней строке показано ускорение, полученное в результате модификации программы. Следует отметить, что выигрыш в быстродействии получается существенный, в частности для n=1000 вместо 8 суток программа решается в течение чуть более двух суток. Таким образом, несмотря на то, что включение содержимого вызываемых функций в вызывающую программу является весьма трудоемкой процедурой и приводит к увеличению размера программы, она может быть рекомендована для случаев, когда предполагается длительное решение.
- Было проведено экспериментальное исследование влияния уровня оптимизации на время решения программ вычисления матриц. Исследовались программы с двумя уровнями оптимизации: O0 (оптимизация отсутствует) и O3 (максимальный уровень оптимизации, включая оптимизацию по быстродействию), результаты эксперимента приведены в таблице 3.
- В верхней строке указаны значения n, задающие число повторений и соответственно время решения программы. Во второй строке указывается время t решения первоначального (немодифицированного) варианта программы в секундах. В третьей строке указано время tm решения модифицированного варианта программы в секундах (в этом варианте содержимое функций вручную встроено в вызывающую программу). В последней строке показано ускорение, полученное в результате модификации программы. Следует отметить, что выигрыш в быстродействии получается существенный, в частности для n=1000 вместо 8 суток программа решается в течение чуть более двух суток. Таким образом, несмотря на то, что включение содержимого вызываемых функций в вызывающую программу является весьма трудоемкой процедурой и приводит к увеличению размера программы, она может быть рекомендована для случаев, когда предполагается длительное решение.
Таблица 3
Время решения программы при различных уровнях оптимизации.
|
Уровень оптимизации |
m=6, n=100 |
m=6, n=200 |
m=6, n=500 |
m=8, n=100 |
m=8, n=200 |
m=8, n=500 |
|
O0 |
694 |
2675 |
17079 |
1701 |
6976 |
44683 |
|
O3 |
472 |
1791 |
11577 |
1085 |
4483 |
28327 |
|
k |
1,47 |
1,49 |
1,48 |
1,57 |
1,56 |
1,58 |
- Из таблицы 3 видно, что применение уровня оптимизации O3 дает выигрыш в быстродействии примерно в полтора раза.
- Таким образом, можно сформулировать следующие рекомендации для решения поставленной задачи. Число процессов np выбирается с учетом выполнения условий: np ≥ nc-1; np является делителем m2; m должно быть кратно m2/np. Если указанным выше условиям удовлетворяют несколько чисел, то выбирается меньшее из этих чисел. Если после выбора np по каким-либо причинам число процессоров будет уменьшено (например, по причине неисправности одного или нескольких узлов), то выбранное ранее np можно не изменять. При составлении программы для вычисления переменных
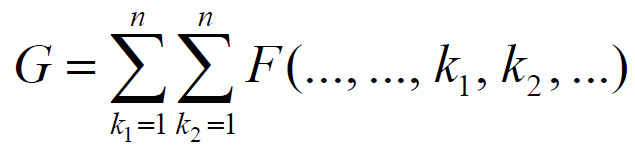 следует по возможности избегать обращений к функциям.
Эти рекомендации позволят обеспечить время решения, близкое к
минимальному для данного кластера, при этом организация внешних
циклов будет максимально простой.
следует по возможности избегать обращений к функциям.
Эти рекомендации позволят обеспечить время решения, близкое к
минимальному для данного кластера, при этом организация внешних
циклов будет максимально простой.- Рассмотрим пример. Пусть требуется вычислить матрицу для m=8 на кластере, имеющем 4 вычислительных узла с 8 процессорными ядрами в каждом узле (nc=32). В соответствии с выше указанными рекомендациями устанавливается np=32. Затем подготавливаются все необходимые исходные файлы. Если неожиданно перед запуском программы выясняется, что работоспособны только 3 узла, то есть реально nc=24, то никаких изменений в подготовленные файлы можно не вносить, значение np=32 не изменяется, и производится запуск с подготовленными параметрами. На каждое процессорное ядро в этом случае будет приходиться в среднем более одного процесса, которые выполняются поочередно. Задача будет решена, время решения при этом будет близко к минимальному для nc=24. Таким образом, мы получим решение за время, близкое к минимальному при данных условиях. Даже если будут работоспособны только 1 или 2 узла, то решение также может быть получено за время, близкое к минимальному. При двух работающих узлах на каждое ядро будет приходиться по 2 процесса, а при одном – 4 процесса.
- Таким образом, в данной работе проведено экспериментальное исследование программ вычисления матриц на мини-кластере. По результатам исследования сформулированы рекомендации для мини-кластеров по выбору числа процессов для программ данного класса, что позволяет получить время решения, близкое к минимальному при данных параметрах мини-кластера.
- Литература:
- Из таблицы 3 видно, что применение уровня оптимизации O3 дает выигрыш в быстродействии примерно в полтора раза.
- Воеводин В.В., Воеводин Вл. В. Параллельные вычисления. – СПб.: БХВ-Петербург, 2002.
- Антонов А. С. Введение в параллельные вычисления. – М.: МГУ, 2002.
- Шпаковский Г.И., Серикова Н. В. Программирование для многопроцессорных систем в стандарте MPI. – Минск: БГУ, 2002.
- Гергель В.П., Стронгин Р.Г. Основы параллельных вычислений для многопроцессорных вычислительных систем: Учебное пособие. - Нижний Новгород, 2003.
- Раков В. С. Многокритериальный выбор вычислительных кластеров // Молодой ученый. 2011. №4. Т.1. С. 97-99.
- Медведик М.Ю., Смирнов Ю.Г. Применение ГРИД-технологий для решения объемного сингулярного интегрального уравнения для задачи дифракции на диэлектрическом теле субиерархическим методом // Известия высших учебных заведений. Поволжский регион. Физико-математические науки. 2008. №2. С. 2-14.
- Смирнов Ю.Г. Применение ГРИД технологий для решения нелинейного объемного сингулярного интегрального уравнения для определения эффективной диэлектрической проницаемости наноматериалов. // Известия высших учебных заведений. Поволжский регион. Физико-математические науки. 2008. №3. С. 39-54.
- Миронов Д.А. Применение суперкомпьютерных вычислительных сред для решения объемного сингулярного интегрального уравнения задачи дифракции на диэлектрическом теле // Известия высших учебных заведений. Поволжский регион. Физико-математические науки. 2009. №2. С. 14-24.
- Гришина Е.Е., Деревянчук Е.Д., Медведик М.Ю., Смирнов Ю.Г. Численное и аналитическое решение задачи дифракции электромагнитного поля на двух секциях с разной диэлектрической проницаемостью, расположенных в прямоугольном волноводе // Известия высших учебных заведений. Поволжский регион. Физико-математические науки. 2010. №4. С. 73-81.
- Романов А. М., Попов Д. С., Стрельников О. И. Запуск задач на вычислительном кластере ВолгГТУ // Молодой ученый. 2011. №6. Т.1. С. 130-133.
- Касперски, К. Техника оптимизации программ. Эффективное использование памяти. – СПб.: БХВ-Петербург, 2003.
- Гербер Р., Бик А., Смит К., Тиан К. Оптимизации ПО. Сборник рецептов – СПб.: Питер, 2010.
- Макконнел, С. Совершенный код. Мастер-класс / Пер. с англ. – Издательско-торговый дом «Русская Редакция»; СПб.: Питер, 2005. – 352 с.