В условиях развивающегося международного сотрудничества увеличивается значение взаимного доверия, а также способов выявления различных нарушений и злоупотреблений. Мошенничества нередко встречаются в международных экономических отношениях, что в глобальном масштабе ведет к потерям миллиардов долларов ежегодно [8, 9]. Одним из способов выявления злоупотреблений в экономической сфере является проверка с участием независимых аудиторов [1]. В России до настоящего времени граждане и государственные учреждения не всегда имели единую точку зрения на мошенничество; иными словами, отмечался конфликт между этическими и законодательными нормами. В то же время, действующие законодательные нормы не всегда эффективно проводятся в жизнь [5]. Подобный подход к международной экономической деятельности может обернуться убытками, если противозаконный характер тех или иных действий станет впоследствии очевидным и доказуемым. В долговременной перспективе поддержание законности в международных экономических отношениях соответствует интересам России, обладающей значительным промышленным потенциалом, территорией и сырьевыми ресурсами. Поэтому желательно, чтобы инициатива раскрытия разного рода злоупотреблений и выяснения сомнительных случаев исходила из нашей страны.
Математическая статистика является одним из методов выявления нарушений в экономической деятельности; она использовалась против отмывания денег, злоупотребления кредитными картами, в области телекоммуникаций [8], в том числе, против несанкционированного входа в компьютерные системы [9] и др. Статистика применялась для выявления недобросовестности научных исследований в области медицины [19,20]. Для борьбы с мошенничеством использовались следующие математические методы: статистическая классификация данных [14, 18], линейный дискриминантный анализ, логистическая дискриминация [9, 17] и др. Классификация с различением подлинных и фальсифицированных данных находит применение для выявления разного рода манипуляций со статистикой [16]. Для подобных целей могут использоваться искусственные нейронные сети [9, 13, 15]. Однако простые методы аудита, такие как пересчет и проверка вычислений, также могут с успехом применяться для выявления манипуляций с количественными данными.
В настоящей статье разбирается случай повторной браковки предприятием (далее – Предприятие) поставленных торговым партнером (далее – Поставщик) партий товара. Текст статьи сформулирован таким образом, чтобы соответствующие фирмы не были идентифицированы. Предприятие регулярно закупало у Поставщика притертые пластиковые пластины, которые применялись для изготовления приборов. Несколько партий пластин были забракованы Предприятием на основании недостаточного качества притирки. Соответствующее количество пластин было поставлено Поставщиком дополнительно.
Заключение о несоответствии № 1, составленное Предприятием, характеризовало забракованную партию из 25.000 притертых пластин, поставленную в 18 коробках. Решение о дефектности поставки было основано на измерениях шероховатости, произведенных на 72 пластинах: по 4 пластины из каждой коробки. В соответствии с инструкцией, отбор образцов для измерений должен был производиться случайно. Шероховатость измерялась по 20 точкам на поверхности пластин с помощью трехмерного лазерного сканирования. Показатель шероховатости Rmax [7], характеризующий качество притирки, представляет собой максимальную высоту выступа профиля по отношению к плоскости, построенной на основании 20 точек, согласно принципу минимальной суммы расстояний от точек до плоскости.
Для статистического анализа 72 обмеренные пластины были разделены на 18 групп соответственно числу коробок. Целью статистического анализа было определение вероятности данного уровня разнообразия (разброса) усредненных показателей шероховатости, характеризующих каждую коробку в отдельности, при условии, что пластины были отобраны из коробок случайно. Расчет проводился с помощью программного обеспечения GraphPad InStat версия 3.00 для Windows, GraphPad Software Inc., США. Нормальность распределения анализируемых 72 показателей шероховатости (P > 0,1) была подтверждена с помощью вышеназванного программного обеспечения на основе метода Колмогорова-Смирнова в адаптации Lilliefor [10, 12].
Статистический анализ включал однофакторный дисперсионный анализ переменных величин (ANOVA), основанный на предположении о нормальности их распределения. Кроме того, к тем же данным был применен непараметрический однофакторный дисперсионный анализ (метод Краскела-Уоллиса), не требующий нормальности распределения изучаемых величин [3, 12]. Уровни значимости (Р), определяемые с помощью обоих методов, отвечают на вопрос: какова вероятность того, что выборочные средние арифметические (характеризующие отдельные коробки) оценивают одну и ту же генеральную среднюю [3]. В применении к разбираемому случаю, этот вопрос можно сформулировать таким образом: какова вероятность данного разнообразия (разброса) усредненных показателей, характеризующих каждую коробку, если образцы для измерений были отобраны из коробок случайно?
Результаты получились следующими. ANOVA: P < 0,0001; метод Краскела-Уоллиса: P < 0,0005. Полученные значения Р соответствуют крайне высокому уровню значимости. Вывод: разброс показателей шероховатости оказался значительно выше, чем можно было бы ожидать при случайном отборе образцов. Если все пластины относятся к одной генеральной совокупности, т.е. изготовлены из одного материала с использованием одинаковой технологии (в соответствии с нормативными документами), вероятность данного уровня разброса показателей составляет менее 0,05 %.
Заключение о несоответствии № 2 характеризовало другую забракованную партию из 67.000 притертых пластин, поставленную в 18 коробках. Решение о дефектности поставки было основано на измерениях шероховатости, произведенных на 36 пластинах: по 2 пластины из каждой коробки. Отбор образцов для измерения должен был проводиться случайно. Методика измерения была та же, что и в первом случае. Нормальность распределения анализируемых 36 показателей шероховатости была подтверждена с помощью вышеназванного программного обеспечения. Поскольку были обмерены только 2 образца из каждой коробки, статистическая значимость результатов была ниже, чем в первом случае. Тем не менее, полученные результаты достаточно убедительны.
ANOVA: P = 0,0106; метод Краскела-Уоллиса: P = 0,0682. Уровень значимости P < 0,05 принято считать статистически достоверным. Вывод: разброс показателей шероховатости выше, чем можно было бы ожидать при случайном отборе образцов. Если все пластины относятся к одной совокупности, т.е. изготовлены из одного материала с использованием одинаковой технологии, вероятность данного уровня разброса показателей составляет около 5 % или меньше.
Для повышения достоверности выводов был использован также другой подход, основанный на следующих предпосылках. Качество притирки или шлифования определяется следующими факторами: сила, прилагаемая к шлифующему инструменту, скорость его вращения, контактная температура, а также свойства абразива [2,4,6]. Очевидно, что при прочих равных условиях, шероховатость обрабатываемой поверхности зависит от размера зерен абразива. Соответственно, кривая распределения рангов показателей шероховатости случайно отобранных пластин должна иметь максимум, определяемый средним диаметром зерен абразива. По обеим сторонам от максимума кривая будет опускаться вниз. Таким образом, следует ожидать следующих корреляций между величиной показателя шероховатости и частотой встречаемости соответствующих рангов этого показателя (при условии случайности отбора образцов из коробок): положительная корреляция от минимального приблизительно до среднего значения и отрицательная – при значениях показателя выше среднего. Для анализа были использованы данные обмера 2 наборов пластин: 1-й набор - 36 пластин из забракованной партии в 18 коробках (согласно заключению о несоответствии № 2) и 2-й набор (контроль) - 150 пластин из принятой партии, где аналогичные измерения были произведены Поставщиком.
Результаты получились следующими. 1-й набор: 36 пластин из общего числа 67.500. Средняя величина показателя шероховатости – 0,0158 мм, стандартное отклонение – 2.
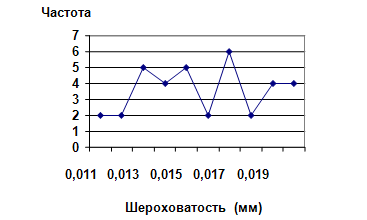
Рис. 1. Показатели шероховатости и абсолютные частоты соответствующих значений этого показателя (для 36 пластин из забракованной партии).
Далее, рис. 1 был разделен на 2 части до и после среднего значения показателя шероховатости. Для первой и второй частей рисунка с помощью вышеназванного программного обеспечения были вычислены коэффициенты линейной корреляции между абсолютными значениями показателей шероховатости и частотой их встречаемости, что в данном случае эквивалентно частоте соответствующих рангов значений показателя (рис. 2-4).
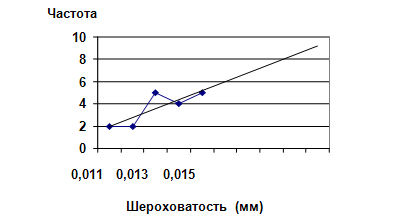
Для 1-го набора пластин (из забракованной партии), в первой половине рисунка коэффициент линейной корреляции составил r = 0,26, что представляет собой слабую положительную корреляцию, лишенную статистической достоверности при данном числе корреляционных пар (n =10).
Рис. 2. Первая половина
рис. 1. Слабая, статистически недостоверная корреляция
между
абсолютными значениями показателей шероховатости их частотой.
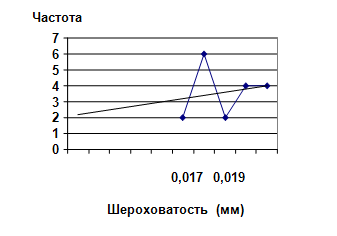
Для второй половины рис. 1 коэффициент линейной корреляции составил r = 0,094, то есть ожидаемая отрицательная корреляция не подтвердилась.
Рис. 3. Вторая половина рис. 1. Слабая, статистически недостоверная корреляция между значениями показателей шероховатости и их частотой.
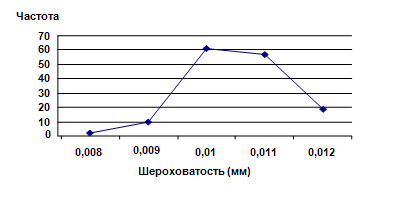
2-й набор пластин (контроль). Средняя величина показателя шероховатости – 0,0105 мм, стандартное отклонение – 0,85. Коэффициенты линейной корреляции для первой (восходящей) и второй (нисходящей) частей кривой составили, соответственно, r1 = 0,9178 и r2 = –0,921; то есть, как и ожидалось, сильные и статистически достоверные корреляции выявлены как для первой, так и для второй частей рисунка.
Рис. 4. Показатели шероховатости и их частоты для 150 пластин из принятой партии.
Таким образом, количественные данные, представленные в заключениях о несоответствии как основание для браковки партий пластин, неточны или были изменены преднамеренно. Если данные замеров правильны, это значит, что отбор пластин из коробок для выполнения замеров производился неслучайно и, по-видимому, имел место поиск бракованных образцов. Настоящий пример показывает, как математическая статистика может быть использована для выявления манипуляций с количественными данными и образцами. Вообще говоря, математическая статистика применима для этой цели, поскольку манипуляции могут приводить к отклонениям от обычного характера распределения количественных данных.
Литература:
Давиа Г.Р. Мошенничество: методики обнаружения (перевод с английского). Санкт-Петербург: ДНК, 2005.
Ермаков Ю.М. Перспективы эффективного применения абразивной обработки. М.: НИИМаш, 1982.
Ивантер Э.В., Коросов А.В. Элементарная биометрия. Петрозаводск: ПетрГУ, 2005.
Обейд А. Исследование динамики шероховатости поверхности стекл ВК7 и ТФ1 при обработке поверхностным притиром // Оптический журнал 2005, №12, стр. 79-82.
Оленев Р.Г. Мошенничество как вид девиантного экономического поведения. Автореферат канд. экон. наук. Санкт-Петербург: Государственный университет экономики и финансов, 2000.
Пилинский В.И., Донец И.П. Производительность, качество и эффективность скоростного шлифования. М.: Машиностроение, 1986.
Суслов А.Г., Корсакова И.М. Назначение и обозначение параметров шероховатости поверхностей деталей машин. Брянск: БГТУ, 2006.
Becker R.A., Volinsky C., Wilks A.R. Fraud detection in telecommunications: history and lessons learned. Technometrics 2010, V 52, N 1, p. 20-33.
Bolton R.J., Hand D.J. Statistical Fraud Detection: A Review. Statistical Science 2002, V 17, N 3, p. 235-255.
Dallal G.E., Wilkinson L. An analytic approximation to the distribution of Lilliefors’ Test statistic for normality. American Statistician 1986, V 40, N 4, 294-296.
Damon R.A., Harvey W.R. Experimental design, ANOVA, and regression. New York: Harper & Row, 1987.
Dudewicz E.J., Mishra S.N. Modern mathematical statistics. New York: John Wiley & Sons, 1988.
Fanning K., Cogger K.O., Srivastava R. Detection of management fraud: a neural network approach. In: Proceedings the 11th Conference on Artificial Intelligence for Applications. IEEE Computer Society Press, 1995, р. 220-223.
Hand D. J. Discrimination and Classification. Chichester: John Wiley & Sons, 1981.
He H.X., Wang J.C., Graco W, Hawkins S. Application of neural networks to detection of medical fraud. Expert Systems with Applications 1997, V 13, p. 329-336.
Kouritzin M.A., Newton F., Orsten S., Wilson D.C. On detecting fake coin flip sequences. In: Ethier, S.N., Feng, J., Stockbridge, R.H. (Editors). Markov Processes and Related Topics: A Festschrift for Thomas G. Kurtz. Beachwood, Ohio: Institute of Mathematical Statistics, 2008, p. 107-122.
Lachenbruch P.A. Discriminant analysis when the initial samples are misclassified. II: Non-random misclassification models. Technometrics 1974, V 16, N 3, p. 419-424.
McLachlan G.J. Discriminant analysis and statistical pattern recognition. New York: John Wiley & Sons, 1992.
Ranstam J., Buyse M., George S.L., Evans S., Geller N.L., Scherrer B., Lesaffre E., Murray G., Edler L., Hutton J.L., Colton T., Lachenbruch P. Fraud in medical research: an international survey of biostatisticians. ISCB Subcommittee on Fraud. Controlled Clinical Trials 2000, v 21, N 5, p. 415-427.
von Elm E. Research integrity: collaboration and research needed. Lancet 2007, V 370, p. 1403-1404.