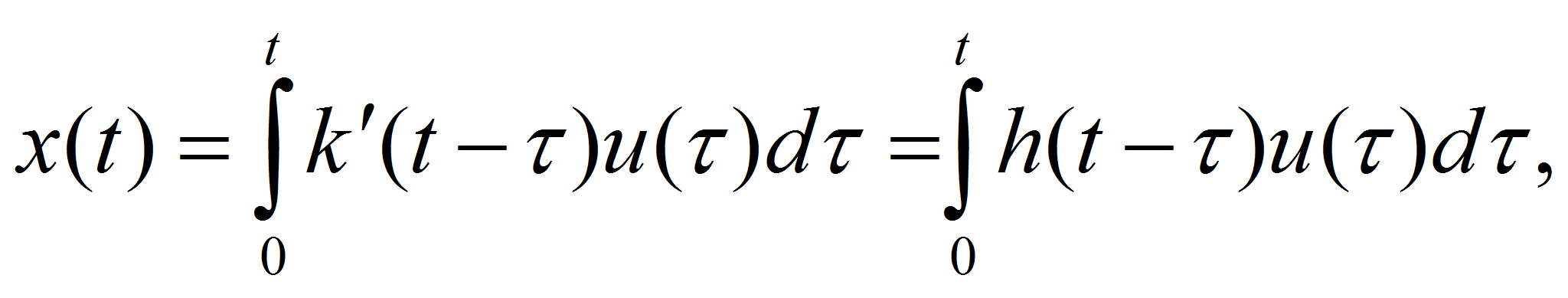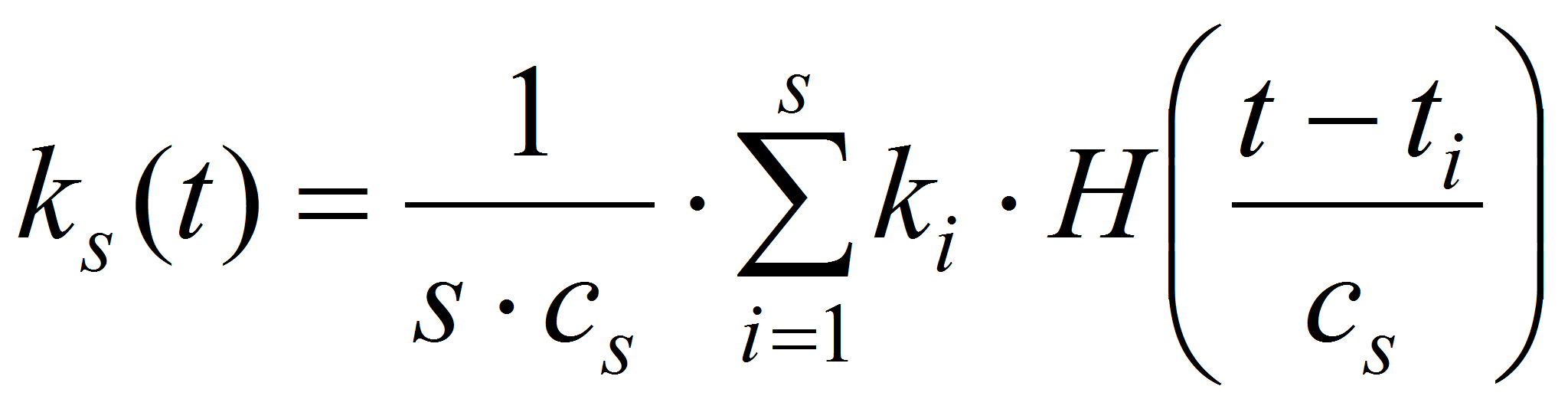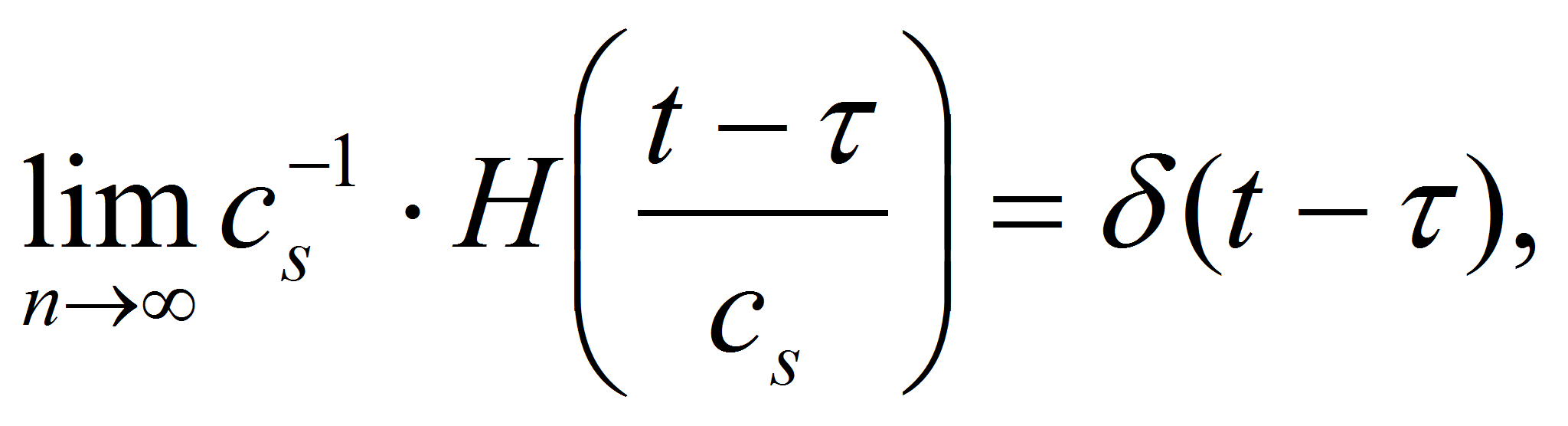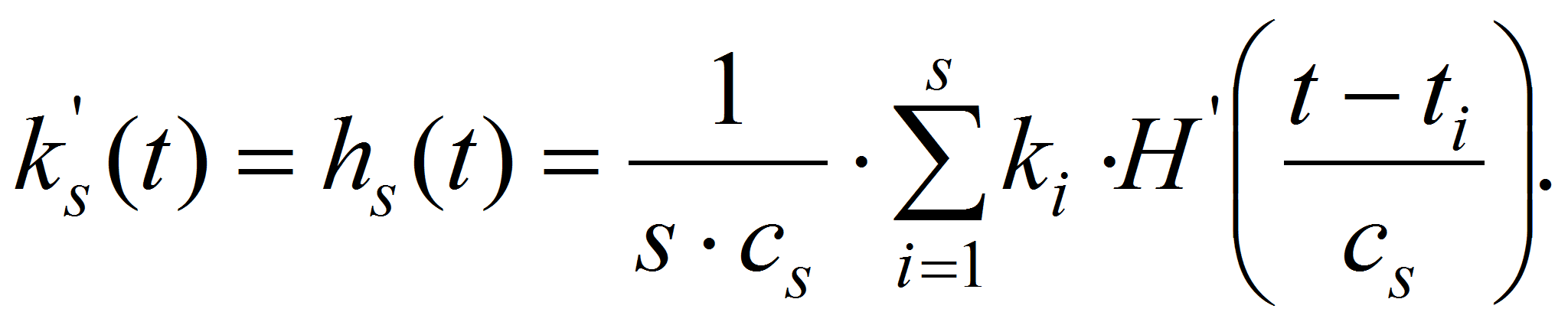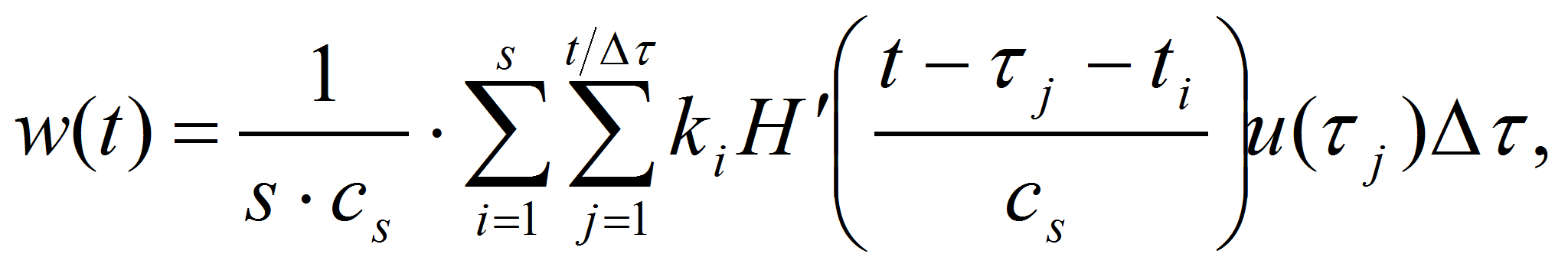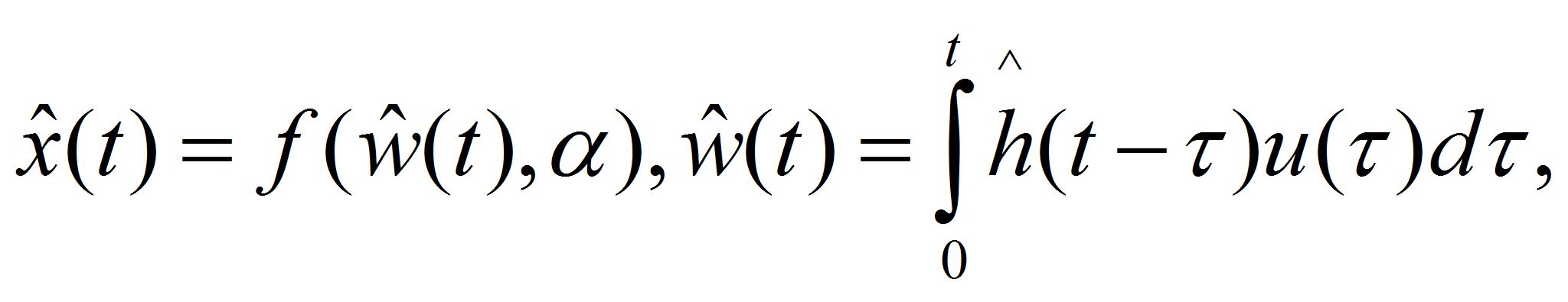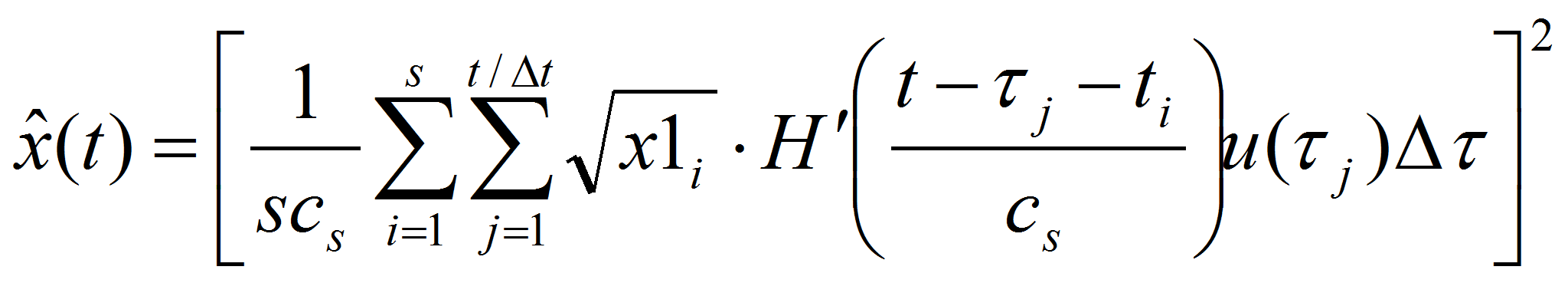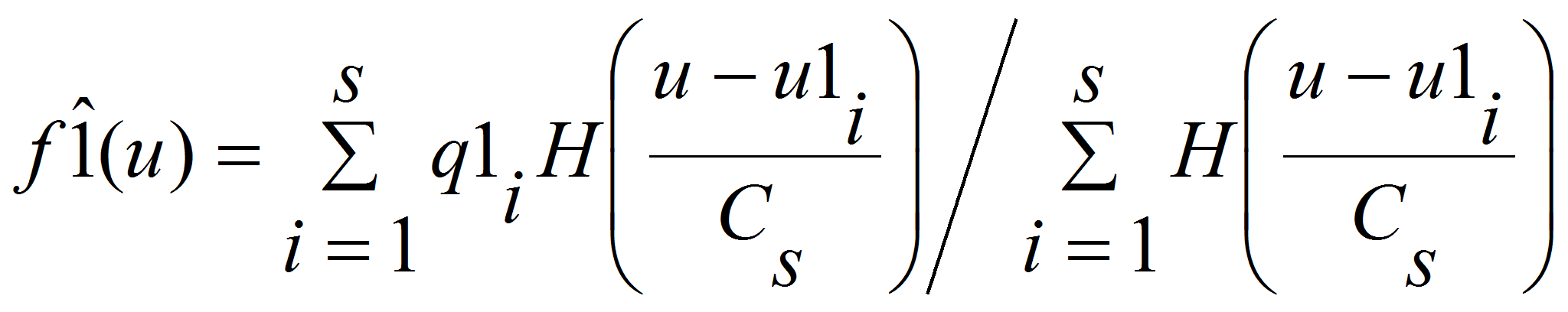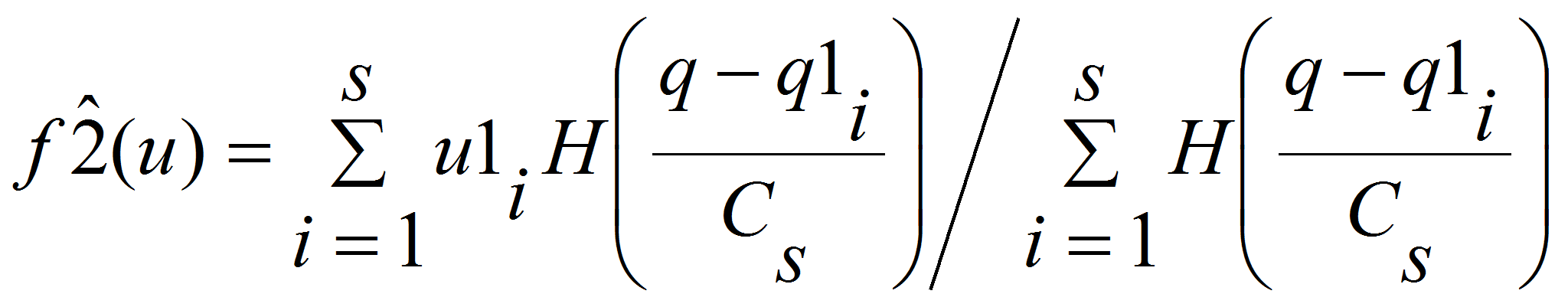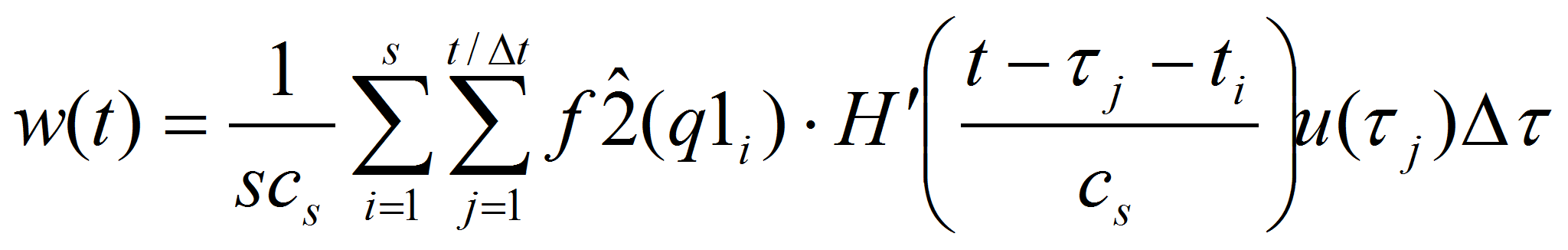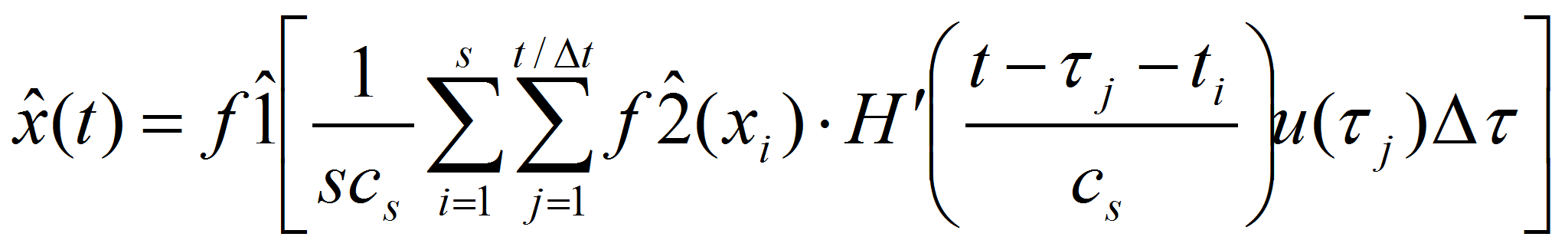Развитие теории и методов математического моделирования нелинейных динамических систем является актуальной проблемой современной прикладной математики. Наиболее важными с точки зрения приложений являются динамические системы, допускающие активный эксперимент при отсутствии полной априорной информации о структуре и параметрах моделируемого объекта.
Для упрощения моделирования нелинейный объект может быть представлен в виде некоторой комбинации линейных динамических и безынерционных нелинейных блоков. В таком случае, модель, которая описывает исследуемый объект с требуемой точностью, представляет собой наилучшую комбинацию линейных, нелинейных элементов и их параметров. Простейшие модели нелинейного динамического объекта представляют собой последовательное соединение двух блоков .[2]
Преимуществом использования таких моделей является их относительная простота притом, что в них нелинейные и динамические свойства исследуемого объекта искусственно разделены и сосредоточены во входном и выходном блоках. [2] Однако, простейшие модели описывают реальный объект лишь приближенно. Основная сложность в построении моделей таких объектов заключается в том, что внутренние сигналы w(t) являются недоступными для измерения.
Пусть исследуемая нелинейная динамическая система представлена в виде двух последовательно включенных звеньев – линейного динамического и нелинейного статического (модель Винера)[3].
Рисунок 1. Модель Винера
Имеется
выборка измерений реакции объекта на тестовое входное воздействие
i=1,s.
Данные о структуре объекта, отсутствуют. Существует возможность
проведения экспериментов.
Рассмотрим два случая:
1. Структура и параметры линейной динамической части системы неизвестны. Предположим некоторый вид нелинейности в объекте – известный с точностью до набора параметров. Нелинейный элемент может представлять собой одно из следующих звеньев:
-. Квадратор, который задан следующим соотношением:
|
|
(1) |
2. Тип нелинейного элемента неизвестен.
На основании имеющейся информации необходимо построить модель данной системы, адекватно описывающую ее поведение при произвольном входном воздействии и наличии аддитивной помехи на выходные данные.
Задача идентификации нелинейной системы может быть разделена на две части. Сначала рассмотрим задачу идентификации линейного элемента (ЛЭ).
Метод построения
непараметрической модели линейной динамической системы (ЛДС) основан
на том, что реакция такой системы
на входное воздействие
описывается интегралом Дюамеля (свертки) [1]:
(2)
где h(t)-весовая функция системы, k(t)-переходная функция этой же системы.
Вычисление значения выхода
объекта
при этом возможно, если известна его весовая функция
h(t). На
практике снятие весовой функции с объекта представляется невозможным.
Поэтому основная идея идентификации ЛДС в условиях непараметрической
неопределенности состоит в непараметрическом оценивании весовой
функции.
Запишем оценку переходной функцию системы в виде стохастической аппроксимации регрессии непараметрического типа следующим образом:
(3)
где
- реально «снятые» значения переходной характеристики
ЛДС, то есть сигнал, получаемый на выходе системы при подаче на ее
вход единичного ступенчатого воздействия 1(t),
-
колоколообразная функция,
- параметр размытости, на которые
накладываются
условия сходимости, которым они должны удовлетворять: [1]
(4)
(5)
Переходная функция h(t) связана с весовой k(t) следующим соотношением[4]
(6)
Непараметрическая оценка весовой функции примет следующий вид:
(7)
Подставив непараметрическую оценку весовой функции в интеграл Дюамеля, получим непараметрическую модель ЛДС. После чего, заменив интеграл его дискретным аналогом (суммой), получим непараметрическую расчетную модель линейного динамического элемента системы:
(8)
где
- переменная интегрирования, которая изменяется с дискретностью
.
Далее рассмотрим алгоритм идентификации нелинейной системы. Предположим, что структура нелинейного элемента задана с точностью до набора параметров, т.е. выход исследуемого объекта вычисляется как некоторая функция от интеграла Дюамеля:
(9)
где x(t)
– выходной сигнал системы;
– выход линейной части системы (не измеряемый); u(t)
– входной сигнал системы; f{}
– нелинейный оператор.
Математическая
модель нелинейного объекта может быть представлена в виде системы
уравнений (8), (9), в которых вместо весовой функции h(t)
и параметров
используются их статистические оценки. Они могут быть получены,
если при тех жe
условиях эксперимента, в которых были получены реализации
,
сформировать выборку
.[3]
В случае, когда для
некоторых классов нелинейных элементов выражение (9) может быть
разрешено относительно
,
имеем:
,
(10)
В данном случае непараметрическая модель нелинейного объекта примет вид:
(11)
Таким образом, в общем виде получен алгоритм, позволяющий строить непараметрические модели нелинейных динамических системы, представленных в виде последовательного соединения линейного и нелинейного звеньев. Данные методы не предусматривают наличия полной априорной информации о структуре объекта.
Идентификация
нелинейной системы с квадратором.
Пусть
имеем систему, представленную в виде модели Винера (Рис. 1). Причем
нелинейная часть системы представляет собой квадратор, описываемый
функцией вида:
c
– const.
Выход объекта вычисляется следующим образом:
.
При единичном входном
воздействие
выход
нелинейной системы равен
.
То есть переходную характеристику линейного элемента
можно
выразить через выход исследуемого процесса следующим образом:
(12)
При произвольном входном воздействии и нулевых начальных условиях выход линейной части системы описывается выражением (8). С учетом рассчитанного значения переходной функции (3) выход линейного элемента равен:
(13)
Модель нелинейного объекта x(t) тогда имеет вид:
(14)
где
– реакция нелинейной системы на единичное входное воздействие,
- тестовое входное воздействие.
Пример 1. Рассмотрим нелинейную динамическую систему, поведение которой имитируется следующим образом: Линейная часть объекта описывается дифференциальным соотношением:
(15)
Нелинейный элемент представляет собой квадратор вида (1) с параметром а=4.37.
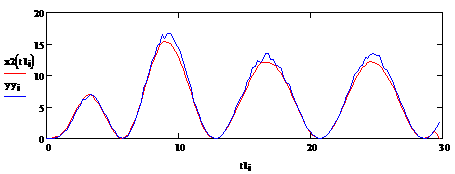
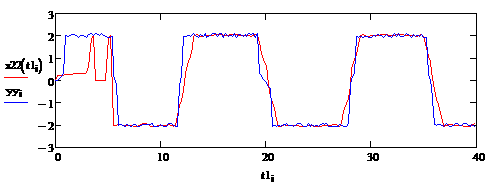
Рис.2. x2(t) - модель нелинейной системы, yyi - выход системы, объем выборки s=150, шаг дискретизации h=0.2, помеха 5%, входное воздействие: u(t)=2cos(0.4t),относительная средняя ошибка моделирования 2.5%
Делая анализ работы модели нелинейного динамического объекта с видом нелинейности типа квадратор, можно сделать следующие выводы: непараметрическая модель адекватно описывает систему при различных значениях параметров нелинейной части объекта, в условиях зашумленности каналов связи, при различном объеме выборки и различных входных воздействиях.
Определение типа
нелинейности моделей Винера.
Пусть
имеется система типа Винера, вид нелинейности которой неизвестен.
Если подать на вход системы
единичное
воздействие, выход ее линейной части w(t)=k(t)
будет
стремиться к некоторой неизвестной константе С1,
а выход нелинейного объекта будет стремиться к величине, равной
f(C1).
При некотором произвольном постоянном входном воздействии
:
,
.
Проведя серию экспериментов над системой, в ходе которых будем
подавать на ее вход различные константы, можем получить выборку
,
(16)
где qi
– установившееся значение выхода системы при входном
воздействии ui.
Причем значения qi
будут пропорциональны f(ui),
т.е.
,
С2=const.
На основании полученной выборки можно построить непараметрическую
оценку функции нелинейного звена объекта:
следующим
образом:[4]
(17)
где q1i – установившееся значение выхода системы при входном воздействии u1i, H(∙) – колоколообразная функция, сs – параметр размытости.
Далее получаем оценку
функции
.
(18)
В общем случае восстанавливается при этом лишь часть нелинейного звена f(p) при p>0, однако необходимо восстановить вид функции при любом аргументе. Для этого предполагаем, что функция нелинейного звена симметрична относительно оси ординат
- f(-p)=f(p) или f(-p)=-f(p).
Таким образом, вид
нелинейности системы находится согласно (17), (18). При этом значения
переходной функции линейного звена объекта k(t)
могут быть рассчитаны следующим образом:
При произвольном входном воздействии модель линейного элемента следующая:
(19)
Выход нелинейного объекта:
Таким образом, непараметрическая модель примет вид:
(20)
где хi – реакция нелинейной системы на единичное входное воздействие, u – тестовое входное воздействие.
Рассмотрим следующую
систему: линейная часть объекта описывается дифференциальным
соотношением:
Нелинейный элемент представляет собой звено насыщения с параметрами: b1=2 v0=0.4
Рис.4. x2(t) - модель нелинейной системы, yyi - выход системы, объем выборки s=150, шаг дискретизации h=0.2, помеха 5%, относительная средняя ошибка моделирования 6.4% , тестовое входное воздействие: u(t)=2cos(0.4t)
Полученная непараметрическая модель адекватно описывает данную систему при различных видах нелинейной части объекта, в условиях зашумленности каналов связи, при различном объеме выборки и входных воздействиях.
- Литература:
Медведев А.В. Непараметрические системы адаптации.–Новосибирск: Наука,1983– 173с.
Попков Ю.С., Идентификация и оптимизация нелинейных стохастических систем, - М.: Энергия, 1976г., 440 с.
Чайка С.Н. К идентификации динамических систем при частично параметризованной структуре модели / Динамика систем: Управление и оптимизация. Горький: Изд-во Горьковского гос. ун-та, 1989.
Эйкофф П., Основы идентификации систем управления, - М.: Мир, 1975г.