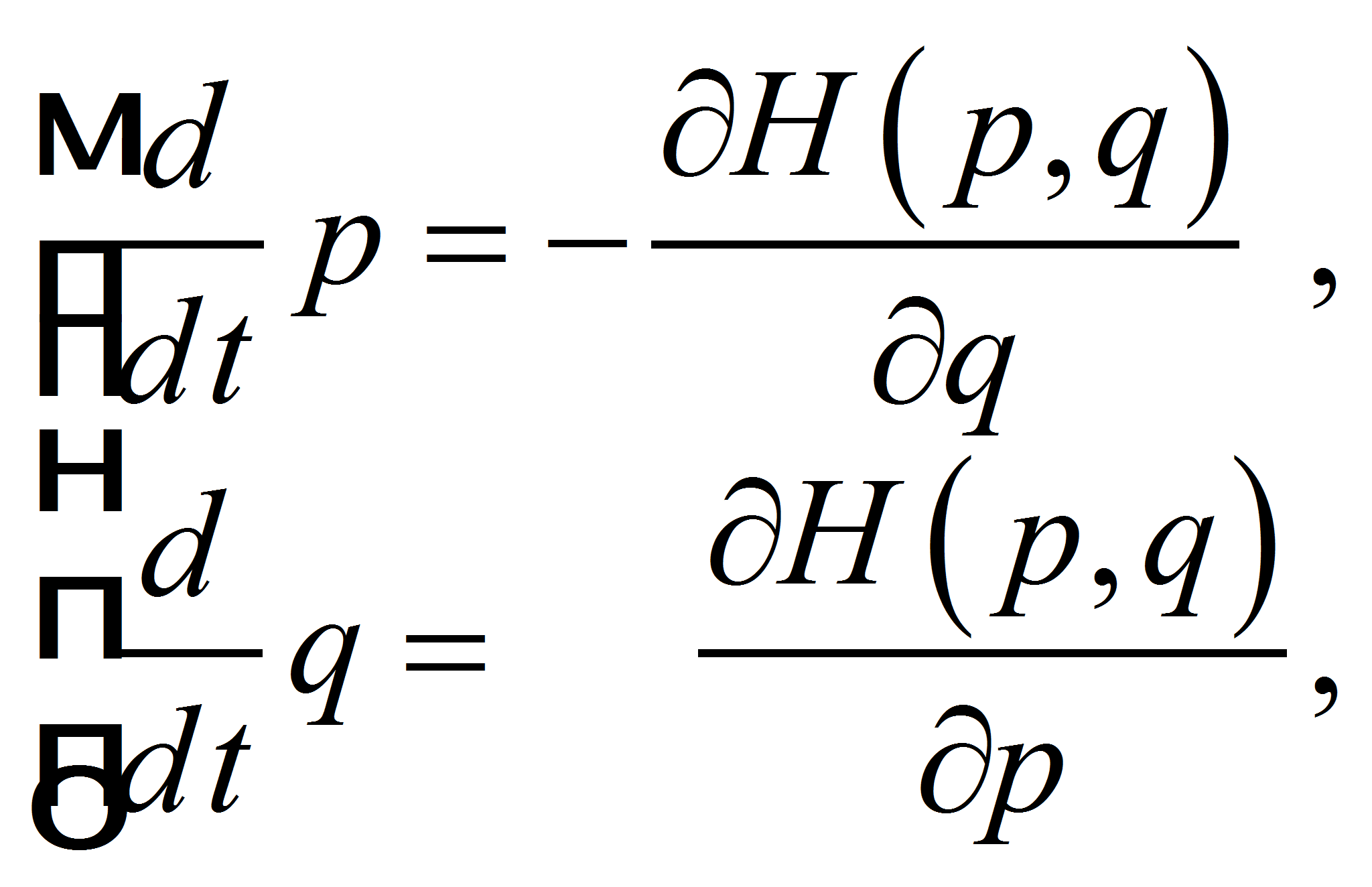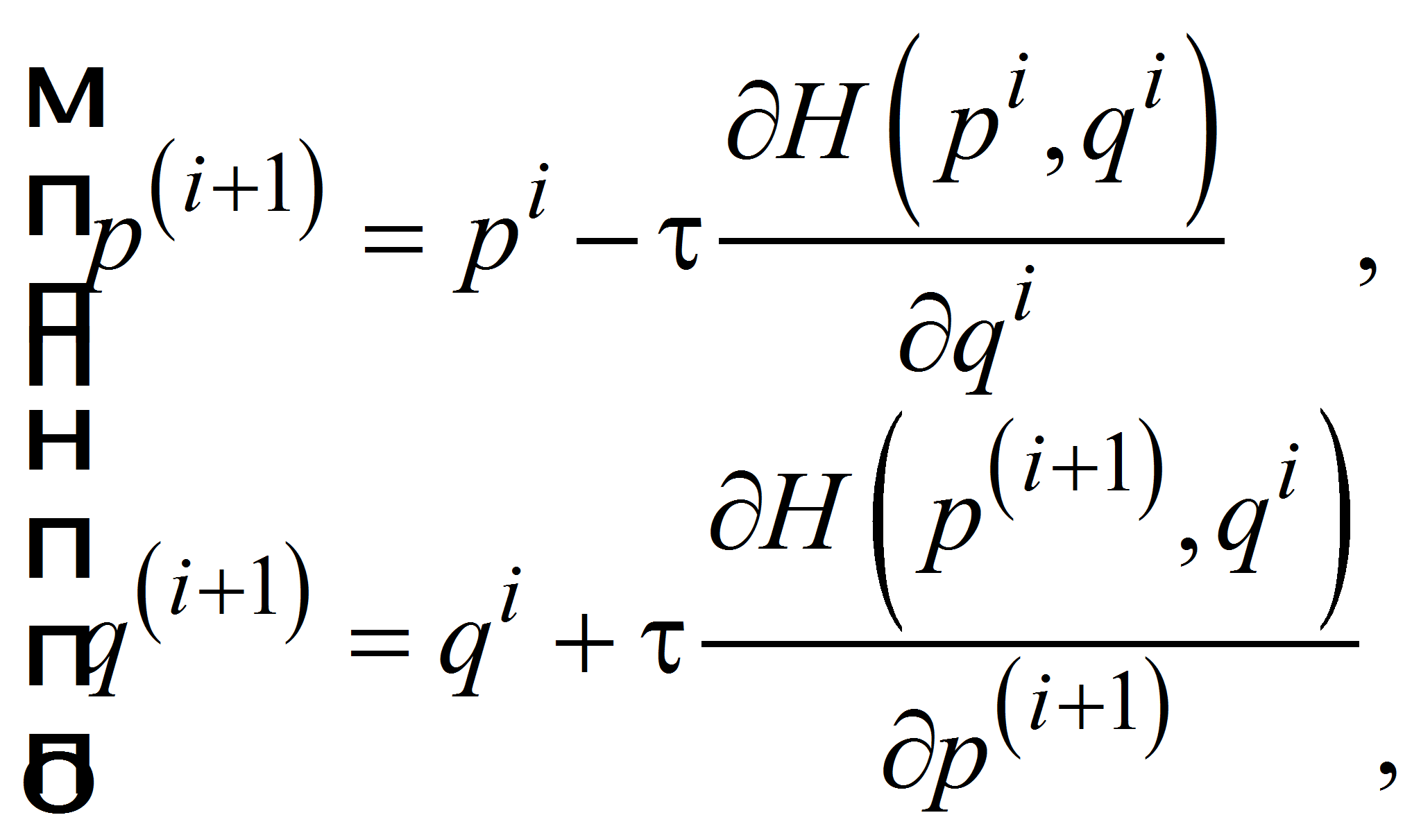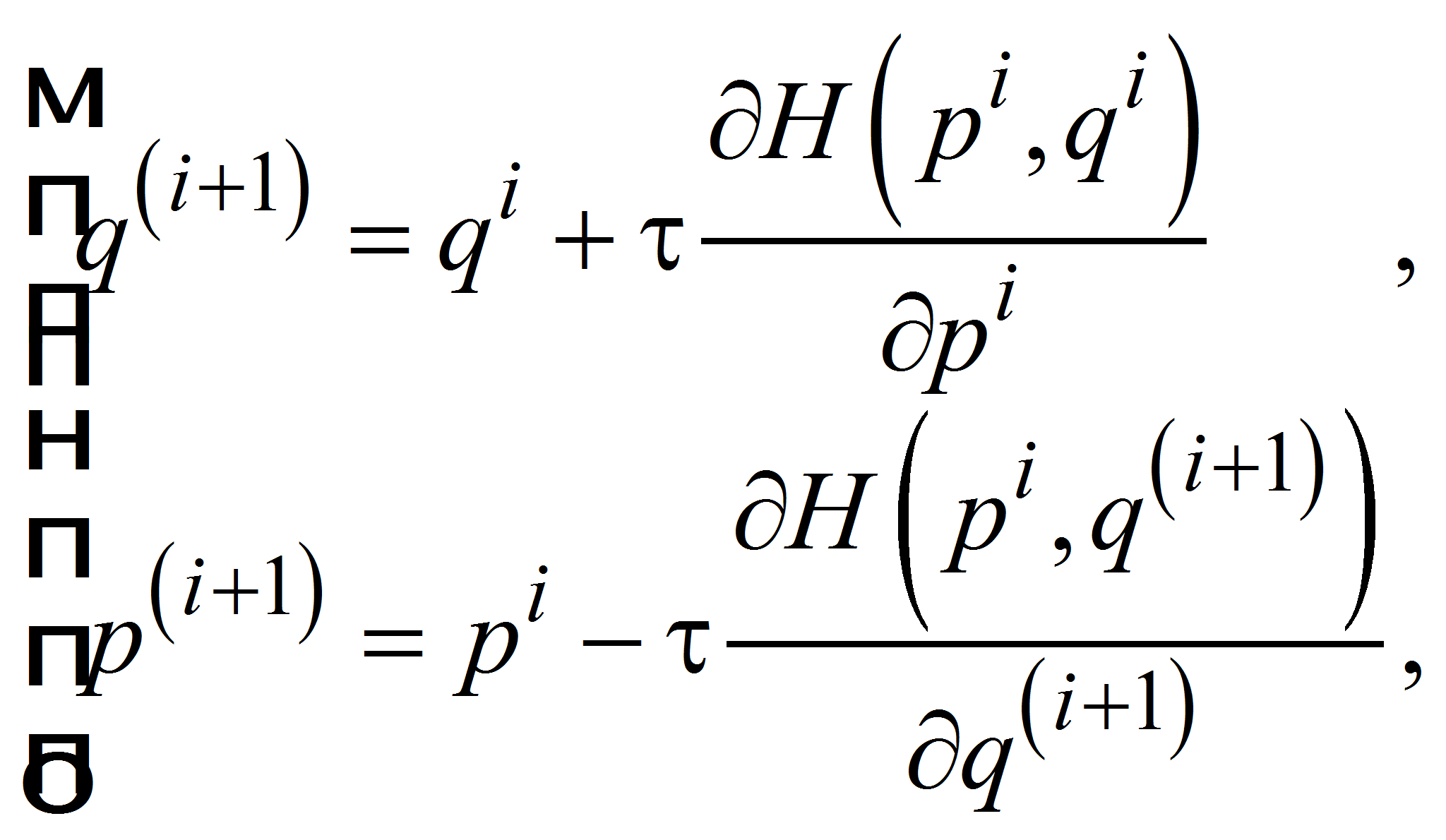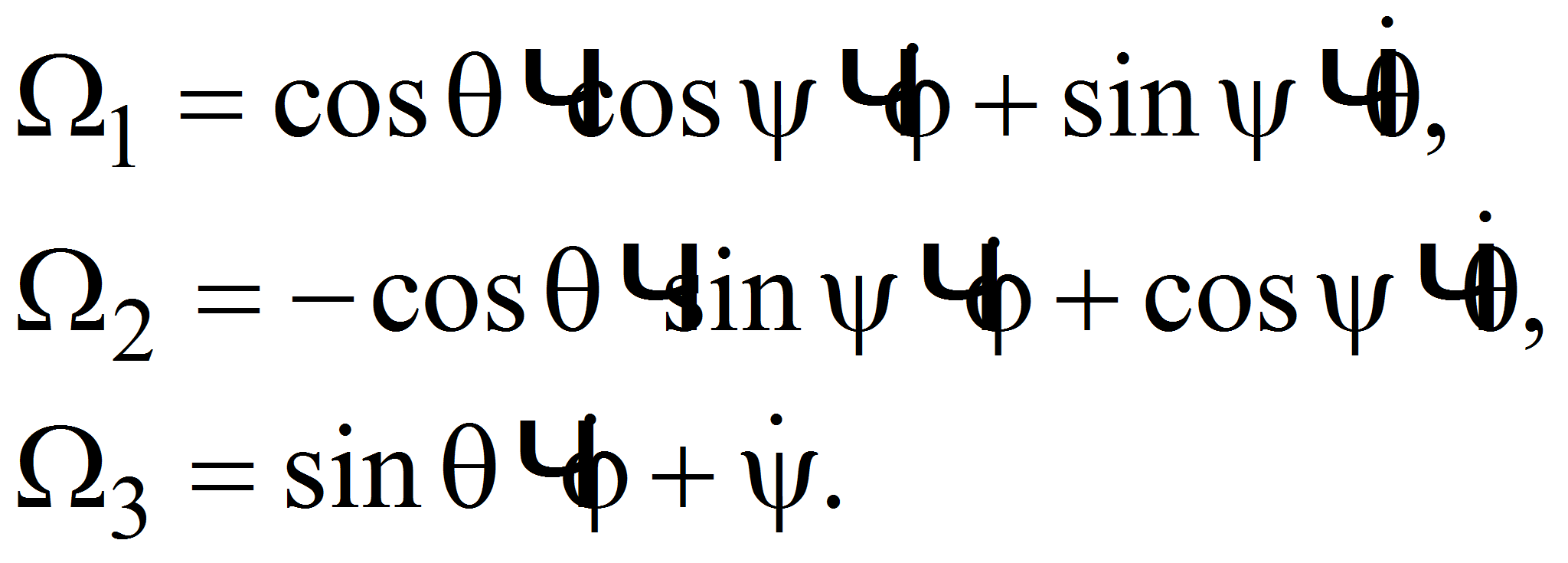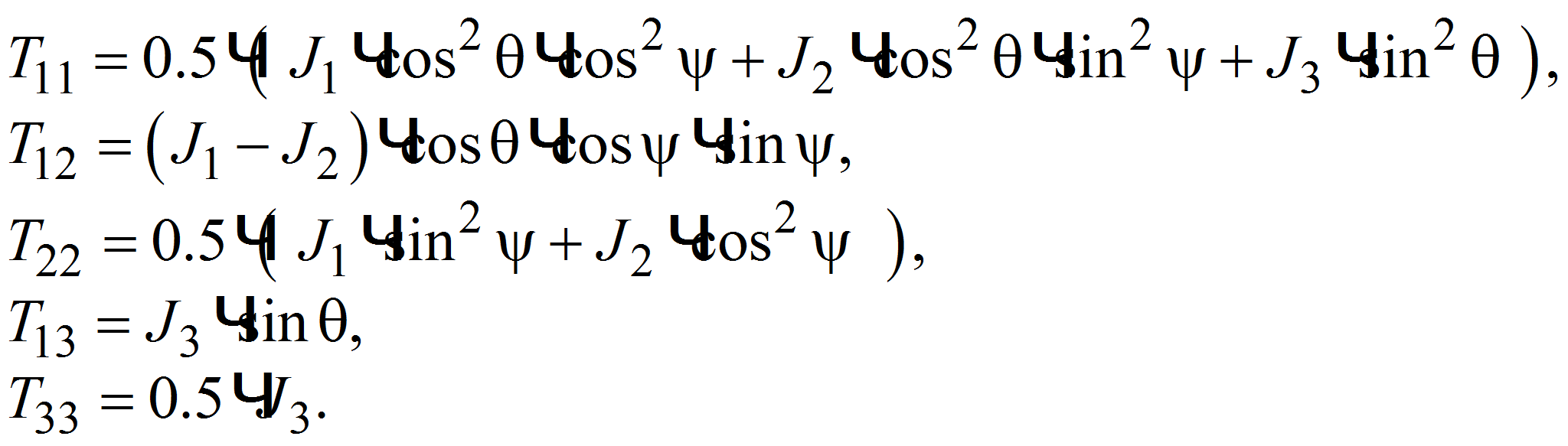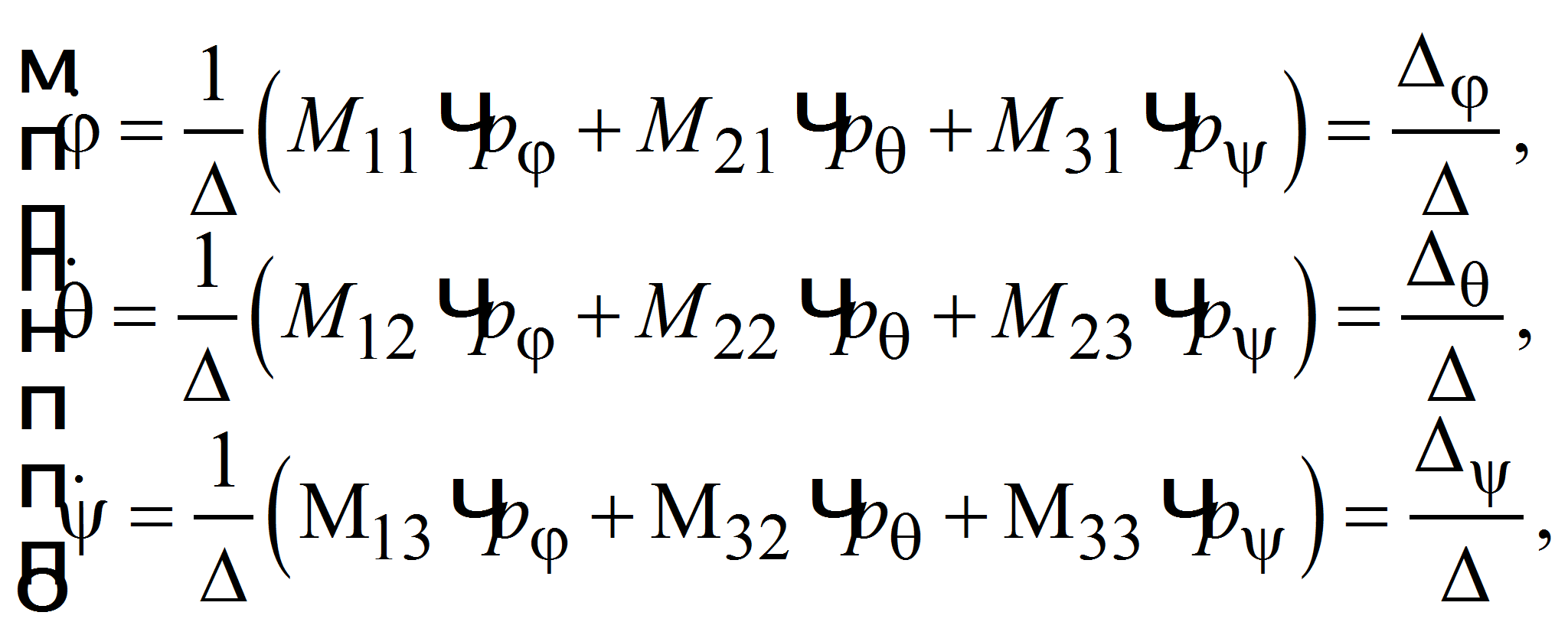При конструировании, создании и последующей эксплуатации систем различного назначения важнейшими вопросами являются исследование условий устойчивости их движения для обеспечения безопасности. Натурное воспроизведение неустойчивых режимов движения связано с большим риском.
Альтернативой является использование математических моделей для описания указанных систем.
Предметом исследования в статье являются математические модели динамики твердого тела в форме уравнений Гамильтона и численные методы их интегрирования, применительно к описанию транспортных, авиационных, космических систем.
Для численного интегрирования уравнений Гамильтона [1] использован канонический метод, в основе которого лежит принцип консервативных возмущений. Согласно этому принципу все вычислительные процессы численного интегрирования уравнений движения должны соответствовать малому консервативному возмущению. Такой подход приводит к значительному повышению достоверности и информативности результатов компьютерного эксперимента. Следуя результатам канонической теории возмущений КолмогороваАрнольдаМозера [2], малые консервативные возмущения не могут нарушать устойчивость консервативной системы при ее движении вблизи положения равновесия.
Неустойчивость консервативно возмущенной системы, воспроизводимая в процессе компьютерного эксперимента, всегда определяет неустойчивость исходной системы. Имеется реальная возможность использования результатов указанной теории в исследовании динамики твердого тела, в частности для определения условий устойчивости летательных аппаратов.
Запишем исходную систему уравнений Гамильтона для невозмущенного движения твердого тела:
|
(1) |
где
![]() функция Гамильтона,
функция Гамильтона,
![]() обобщенные импульсы и координаты.
обобщенные импульсы и координаты.
Связь между исходной и
консервативно возмущенной системой осуществляется бесконечно малыми
каноническими преобразованиями.
Этому соответствуют алгоритмы
численного интегрирования, обеспечивающие консервативность возмущения
в форме импульс – координата (2) и координата – импульс
(3):
|
(2) |
(3) |
На основе использования алгоритмов (2), (3) построены компьютерные модели, воспроизводящие движение твердого тела в условиях свободного вращения в потенциальном поле.
Представим физическую
модель объекта как свободное вращение твердого тела вокруг точки,
относительно неподвижной системы координат
![]() ,
а в качестве углов
,
а в качестве углов
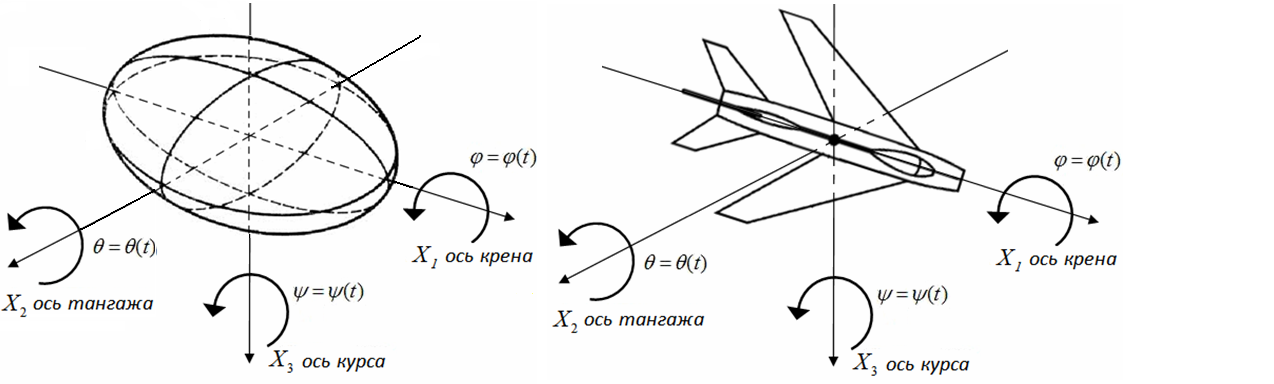
![]() выберем навигационные углы поворота относительно оси крена, тангажа и
курса (рисунок 1).
выберем навигационные углы поворота относительно оси крена, тангажа и
курса (рисунок 1).
Рис. 1. Навигационные углы вращения летательного аппарата
Для записи
кинематических формул летательного аппарата необходимо определить
проекции угловой скорости на оси подвижной системы координат
![]() ,
выразив их через углы поворота
,
выразив их через углы поворота
![]() и их производные
и их производные
![]() .
.
Получим выражение проекций
угловых скоростей твердого тела
![]() на оси подвижной системы координат
на оси подвижной системы координат
![]() [3]:
[3]:
|
(4) |
Если
главные моменты инерции твердого тела отнесены к осям системы
![]() ,
то кинетическая энергия вращения выразится квадратичной формой вида:
,
то кинетическая энергия вращения выразится квадратичной формой вида:
|
(5) |
Схема построения функции
Гамильтона, заключается в преобразовании производных функции
навигационных углов
![]() в обобщенные импульсы
в обобщенные импульсы
![]() .
.
|
(6) |
Используя выражения для преобразования координат, запишем кинетическую энергию твердого тела в случае свободного вращения:
|
(7) |
где значения коэффициентов квадратичной формы имеют вид:
|
(8) |
Определим
проекции кинетического момента (обобщенные импульсы) через
производные функций углов поворота
![]() и разрешим полученную систему, используя формулу Крамера:
и разрешим полученную систему, используя формулу Крамера:
|
((9) |
((10) |
где
![]() определители системы (9),
определители системы (9),
![]()
алгебраические дополнения.
алгебраические дополнения.
Подставляя выражения
производных функций углов поворота (10) в функцию кинетической
энергии (7), получим функцию Гамильтона
![]() для случая свободного вращения:
для случая свободного вращения:
|
(11) |
В
динамические уравнения Гамильтона входят частные производные функций
Гамильтона
![]() по импульсам и координатам и представляют собой достаточно громоздкие
выражения, поэтому предварительно следует определить соответствующие
частные производные всех промежуточных выражений. При создании и
тестировании компьютерных программ эти промежуточные выражения удобно
представить как упорядоченную систему функций (банк функций) в
табличном виде [4].
по импульсам и координатам и представляют собой достаточно громоздкие
выражения, поэтому предварительно следует определить соответствующие
частные производные всех промежуточных выражений. При создании и
тестировании компьютерных программ эти промежуточные выражения удобно
представить как упорядоченную систему функций (банк функций) в
табличном виде [4].
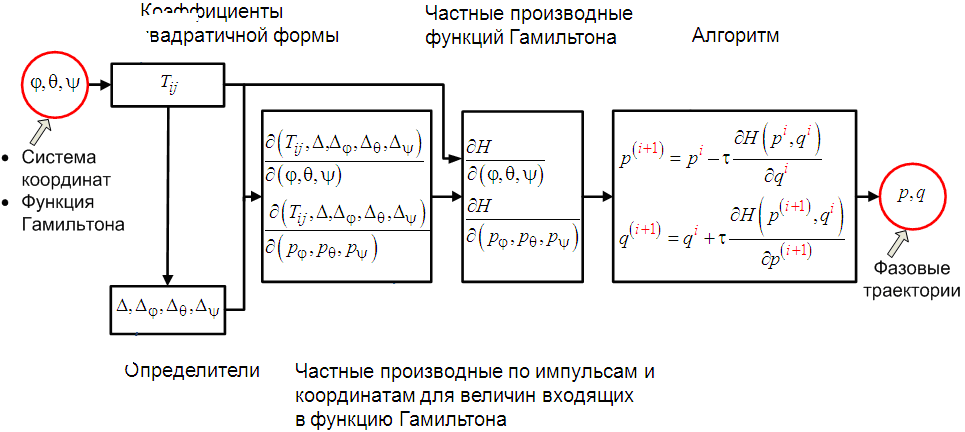
Алгоритм интегрирования может быть представлен в виде следующей схеме (рисунке 2).
Рис. 2. Схема формирования системы функций и алгоритма
Разработанная схема обобщает построение алгоритмов для различных видов углов поворота и систем координат.
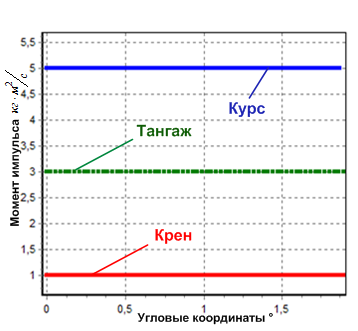
Фазовые траектории для случая свободного вращения летательного аппарата изображены на рисунке 3.
Рис. 3. Фазовые траектории свободного вращения
Воспроизводимое компьютером движение соответствует движению исходной системы в условиях действия консервативных возмущений. Действительно консервативные возмущения, вызванные процессом счета, не нарушают исходную устойчивость движения [5].
При движении в
потенциальном поле к функции Гамильтона добавим потенциальную энергию
![]() .
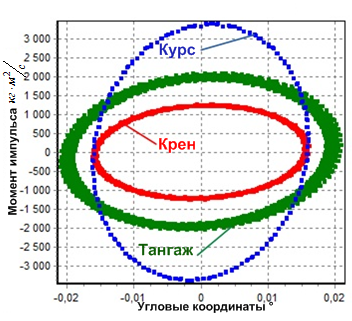
Фазовые траектории при длительных временах наблюдений описывают
устойчивые колебаниям относительно трех осей и представлены на
рисунке 4.
.
Фазовые траектории при длительных временах наблюдений описывают
устойчивые колебаниям относительно трех осей и представлены на
рисунке 4.
Рис. 4. Фазовые траектории движения в потенциальном поле
Консервативные возмущения, вызванные процессом счета, не нарушают устойчивость режима движения твердого тела, то есть движение осуществляется в окрестности точки минимума потенциальной энергии.
Под устойчивым режимом движения будем понимать способность объекта сколь угодно долго оставаться в фиксированной окрестности невозмущенной фазовой траектории при действии на него малых возмущающих факторов.
При движении с диссипацией
энергии к первому уравнению системы (1) добавим диссипативную
составляющую
![]() .
На рисунке 5 представлены фазовые траектории в виде асимптотически
сходящейся спирали.
.
На рисунке 5 представлены фазовые траектории в виде асимптотически
сходящейся спирали.
Рис. 5. Фазовые траектории движения в потенциальном поле
под действием диссипативных сил
Математическая модель движения твердого тела [5] построенная на основе, фундаментальных положений аналитической динамики, позволяет исследовать его поведение в условиях свободного вращение, под действием консервативных и диссипативных сил. Алгоритмы численного интегрирования уравнений Гамильтона, устойчивы к накоплению погрешности во времени, повышают точность решения и быстродействие, что подтверждается малой относительной величиной изменения гамильтониана и наименьшим числом используемых арифметических операций. Программный комплекс моделирования и исследования динамической устойчивости летательного аппарата [6] использован для сравнительной характеристики устойчивости движения твердого тела по методу Эйлера и по каноническому методу.
- Литература:
Ефимов И.Н., Морозов Е.А. Каноническое интегрирование динамических систем. Екатеринбург-Ижевск: Изд-во Института экономики УрО РАН, 2006. – 198 с.
Мозер Ю. КАМ – тория и проблема устойчивости. – Ижевск: ИРТ, 2001. – 448 с.
Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. – М.: Наука, 1977. – 832 с.
Ефимов И.Н., Морозов Е.А., Селиванов К.М., Ермолаева Е.В. Канонические преобразования фазового пространства в динамике твердого тела // Вестник ИжГТУ. – 2009. − №4. − С. 190−195.
Селиванов К.М. Канонический метод интегрирования в исследовании движения твердого тела // Интеллектуальные системы в производстве. 2010. – № 1. – С. 67–76.
Якимович Б.А., Ефимов И.Н., Морозов Е.А., Ермолаева Е.В., Селиванов К.М. Программно-методический комплекс моделирования и исследования динамической устойчивости летательного аппарата // Фундаментальные и прикладные проблемы приборостроения, информатики и экономики: сб. науч. тр. XII Международной научно-практической конференции. – М.: МГУПИ, 2009. – С. 193–197.