В обучении высшей математике в вузе весьма актуальной задачей является обеспечение доступности усвоения новых математических идей, понятий, методов, в частности, желательно чтобы вычислительная (количественная) сторона не заслоняла содержательной (качественной) стороны изучаемого материала. В решении этой задачи обучения важную роль играют средства обучения математике.
Общеизвестно, что для оптимизации и управления процессом обучения должны использоваться такие средства обучения, как приборы и модели, печатные средства, экранные средства, контрольно-обучающие устройства и технические средства обучения.
Специфика обучения математики такова, что основным средством обучения служат задачи и упражнения, которые выступают не только как носители математического содержания, но и как носители математической деятельности, составляющей математический стиль мышления. Для формирования как содержательной, так и процессуальной оставляющей теории вероятностей и математической статистики, необходимо решить достаточное количество задач и упражнений. Только в этом случае представления, понятия, методы, алгоритмы станут инструментами мышления обучаемого.
При изучении таких разделов высшей математики, как теория вероятностей и математическая статистика вычислительная сторона задач отнимает у студентов столько сил и времени, что на осознание содержательной стороны нового учебного материала их уже не хватает. Это обнаруживается, например, при изучении таких тем, как элементы комбинаторики, теорема умножения вероятностей и ее следствия, дискретные случайные величины, проверка статистических гипотез, линейная корреляция и т.п. Объемные вычисления не позволяют в ограниченное несколькими часами время рассмотреть достаточное количество задач для формирования требуемого уровня знаний и умений по конкретной теме у всех студентов, слабые остаются за бортом.
Приведем примеры некоторых задач.
Задача 1. Студент Козлов плохо подготовился к экзамену по математике, но не отчаивается, т.к. рассчитывает получить подсказки от своих друзей: Иванова, Петрова и Сидорова. Первый, второй и третий могут подсказать правильный ответ с вероятностями 3/10, 2/5 и 1/2 соответственно. Если Козлов получит три подсказки, то он сдаст экзамен наверняка. Если он получит две, одну и ни одной подсказки, то сдаст экзамен с вероятностями 3/5, 1/4 и 1/10 соответственно. Козлов сдал экзамен. Какова вероятность того, что он получил одну подсказку? Ответ: искомая вероятность равна 0,30137.
Задача 2. Пять студентов пересдают экзамен. Вероятность пересдачи для каждого из них равна соответственно 0,95; 0,60; 0,75; 0,5 и 0,65. Найти закон распределения числа студентов, успешно пересдавших экзамен, математическое ожидание, дисперсию, начальные и центральные моменты до четвертого порядка включительно. Ответ: см. второй рисунок.
Задача 3. Дана выборка из ста чисел: 44,73; 49,87; 5,00; 34,02; 22,26; 50,33; 63,24; 68,95; 56,52; 49,19; 56,08;52,41; 50,26; 46,67; 61,10; 52,39; 43,22; 60,31; 42,34; 44,15; 49,55; 31,33; 53,88; 60,66; 58,07; 51,44; 30,28; 27,86; 54,47; 52,31; 58,82; 63,32; 24,85; 47,03; 49,67; 44,29; 50,44; 62,19; 19,26; 36,32; 22,61; 41,76; 64,22; 28,50; 44,18; 31,68; 43,25; 54,81; 41,11; 43,46; 78,26; 70,63; 33,25; 50,92; 100; 52,66; 61,19; 57,53; 48,35; 76,06; 41,11; 52,37; 69,26; 69,70; 24,68; 36,33; 39,85; 37,13; 60,70; 61,19; 34,37; 54,20; 45,94; 77,31; 49,94; 74,89; 49,07; 67,92; 21,02; 29,33; 46,40; 52,36; 34,81; 55,96; 29,96; 39,80; 55,93; 72,00; 23,63; 54,72; 65,32; 61,70; 55,05; 49,77; 48,19; 35,27; 23,17; 78,75; 55,82; 66,37. Проверить гипотезу о нормальном распределении с помощью критерия Пирсона при уровне значимости 0,05. Ответ: см. последний рисунок.
Если студентов в первой или второй задаче будет шесть или больше, то их решения займет больше времени. В третьей задаче значений непрерывного количественного признака может быть больше, например, 200, 300, 1000. Если указанные в первых двух задачах вероятности были равны, то применялась бы формула Бернулли. В указанных условиях требуется применить теоремы сложения и умножения вероятностей, что для 4,5 и более событий ведет к громоздким вычислениям. В задаче 2 обработка статистического ряда и вычисление его числовых характеристик также занимает много времени.
Компенсировать вычислительную сложность задач можно с помощью компьютера и табличного процессора Excel. Эффективность применения компьютеров обусловлена следующими факторами: быстрота и надежность обработки любого вида информации; возможность представления информации в графической форме; хранение и быстрота подачи больших объемов информации; возможность моделирования с помощью компьютера разнообразных процессов; активизация содержательной, операционной и мотивационной сторон процесса обучения; оперативное управление учебной деятельностью учащихся; возможность оптимально дифференцировать учебную деятельность школьников в зависимости от уровня подготовки, познавательных интересов и т.д.; организация оперативного контроля и помощи учащимся со стороны учителя; возможность проводить различные математические эксперименты.
Ясно, что при первоначальном знакомстве с теоремами сложения и умножения вероятностей, числовыми характеристиками статистического ряда, алгоритмом проверки статистических гипотез студентам обязательно нужно осознанно прорешать ряд упражнений вручную. Применение калькулятора или компьютера на начальном этапе изучения новой формулы или алгоритма принесет больше вреда, чем пользы, т.к. важно понять как и почему работают и применяются в данной ситуации конкретные формулы и алгоритмы.
Конечно, для профессиональной статистической обработки результатов экспериментов есть специализированные программные средства, а для написания контрольно-обучающих программ есть более подходящие средства, чем Excel, однако последний можно с успехом использовать не только для этой цели.
Во-первых, преподаватель может использовать Excel для подготовки к занятиям. Для составления необходимого задачного материала, например, можно применить генераторы псевдослучайных чисел, в частности, с помощью «генератора задач» достаточно просто выполнить проверку решения или подбор «хороших» ответов.
Во-вторых, подачу массивов статистических данных, динамических иллюстраций, экспериментов, использующих генераторы случайных чисел, преподаватель может осуществлять с помощью Excel.
В-третьих, Excel можно использовать как средство изучения материала теории вероятностей и математической статистики. Студент может разработать как свою собственную Excel-программу для вычисления вероятностей, обработки статистических данных и их наглядного представления, так и воспользоваться готовой программой, например, разработанной преподавателем. Данная программа может использоваться для решения задач типового расчета. Если же студенту необходимо указать полное решение, то он может использовать Excel для проверки правильности решения задач, перед тем как сдавать их на проверку преподавателю.
Для подобного использования компьютера при обучении теории вероятностей и математической статистике автором статьи разработана Excel-программа, которая может быть использована и студентами, и преподавателями.
Программа содержит 15 листов: комбинаторика, формула Байеса, формула Муавра-Лапласа, ДСВ-1, ДСВ-2, генератор «выборка 100», расчет «выборка 100», расчет статистического ряда, расчет «выборка 10 000», перерасчет «выборка 10 000», выборка 10 000, генератор корреляционных таблиц 5 на 5, расчет корреляционных таблиц 5 на 5, расчет корреляционных таблиц 20 на 20, черновик.
На листе «Комбинаторика» можно посчитать перестановки, размещения и сочетания с повторениями и без них. Для перестановок с повторениями количество повторяющихся элементов не должно превосходить 10 (для практических нужд достаточно). Программой проверяется правильность вводимых в формулу аргументов. В случае небольших чисел студент может проверить правильность вычислений на бумаге, а в случае больших аргументов удается сэкономить время для решения других задач.
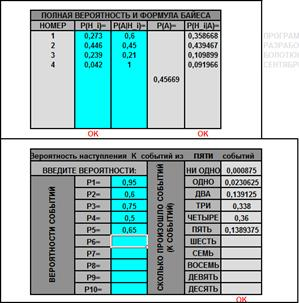 На листе «Формула Байеса» можно посчитать полную вероятность и новые вероятности гипотез, а также вероятности одновременного наступления нескольких событий из не более чем 10 событий (у каждого события может быть задана своя вероятность). Для формулы Байеса число гипотез не должно превосходить 10. Проверяется правильность вводимых аргументов. Возможность расчета вероятности одновременного наступления нескольких событий существенно экономит время. Задачи с такими вероятностями интересны, но редки, видимо, по причине громоздкости вычислений (см. задачу 1).
На листе «Формула Байеса» можно посчитать полную вероятность и новые вероятности гипотез, а также вероятности одновременного наступления нескольких событий из не более чем 10 событий (у каждого события может быть задана своя вероятность). Для формулы Байеса число гипотез не должно превосходить 10. Проверяется правильность вводимых аргументов. Возможность расчета вероятности одновременного наступления нескольких событий существенно экономит время. Задачи с такими вероятностями интересны, но редки, видимо, по причине громоздкости вычислений (см. задачу 1).
На листе «формула Муавра-Лапласа» можно проводить вычисления по локальной и интегральной формулам Муавра-Лапласа, формуле Бернулли. Необходимые промежуточные значения вычисляются автоматически.
 На листе «ДСВ-1» можно получить значения всех основных числовых характеристик (среднее, дисперсия, среднее квадратическое отклонение, начальные и центральные моменты до четвертого порядка включительно) для закона распределения дискретной случайной величины, содержащего не более чем 100 значений ДСВ. Понятно, что возможность расчетов с таким количеством аргументов (возможен непосредственный расчет) не должна освобождать студентов от знания формул для расчета характеристик
На листе «ДСВ-1» можно получить значения всех основных числовых характеристик (среднее, дисперсия, среднее квадратическое отклонение, начальные и центральные моменты до четвертого порядка включительно) для закона распределения дискретной случайной величины, содержащего не более чем 100 значений ДСВ. Понятно, что возможность расчетов с таким количеством аргументов (возможен непосредственный расчет) не должна освобождать студентов от знания формул для расчета характеристик 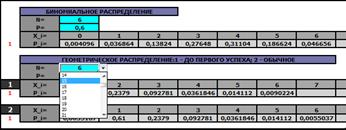 показательного, биномиального и геометрического законов распределения.
показательного, биномиального и геометрического законов распределения.
На листе «ДСВ-2» можно получить статистические ряды биномиального и геометрического законов распределения, задаваемые числом испытаний и вероятностью успеха (получается копируемая таблица, которую можно вставить на лист «ДСВ-1»).
На листе «Генератор «выборка 100» можно получить 100 значений равномерно, нормально или показательно распределенного количественного признака в заданных пользователем пределах. На этом же листе автоматически рассчитывается таблица с группированными данными: концы интервалов, их середины, частота и частость, компоненты среднего и среднее, компоненты дисперсии и дисперсия, теоретические частоты и частости, компоненты критерия согласия Пирсона, теоретическое значение (по заданному пользователем уровню значимости) и наблюдаемое его значение. Кроме указанных значений рассчитываются доверительные интервалы для математического ожидания и среднего квадратического отклонения нормально распределенного количественного признака, начальные и центральные моменты до четвертого порядка включительно, асимметрия и эксцесс. Делается вывод о принятии нулевой или альтернативной гипотезы о виде закона распределения. Строится гистограмма.
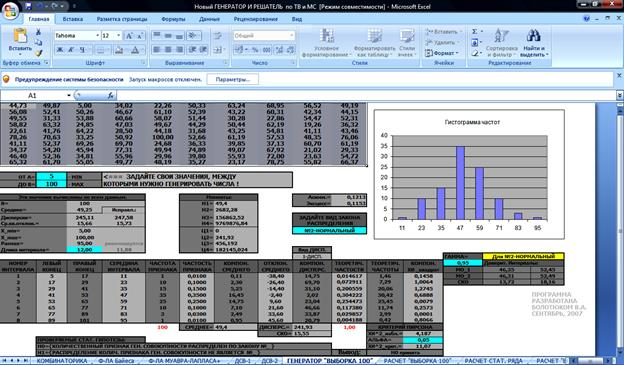 На листе «Расчет «выборка 100» вычисляется тоже, что и на предыдущем листе, но выборка из 100 элементов задается пользователем. Меняя закон распределения на этом листе можно проверить три гипотезы за несколько секунд, т.к. изменение этого параметра меняет не выборку, а формулы, по которым рассчитываются теоретические вероятности. Строится гистограмма.
На листе «Расчет «выборка 100» вычисляется тоже, что и на предыдущем листе, но выборка из 100 элементов задается пользователем. Меняя закон распределения на этом листе можно проверить три гипотезы за несколько секунд, т.к. изменение этого параметра меняет не выборку, а формулы, по которым рассчитываются теоретические вероятности. Строится гистограмма.
На листе «Расчет статистического ряда» производятся вычисления аналогичные вычислениям предыдущего листа, но исходные данные вводятся не в виде выборки, а в виде статистического ряда из восьми элементов (соответствует объему выборки в 100 элементов). Строится гистограмма.
Негибкость вычислений предыдущих листов компенсируется листами «Выборка 10 000» и «Расчет выборки 10 000». Содержимое этих двух листов позволяет проводить вычисления полностью аналогичные вычислениям листа «Расчет «выборка 100», но для выборок с количеством элементов до 10 000. Имеется возможность выбора равномерного, нормального или показательного закона для проверки гипотезы о виде закона распределения. Строится гистограмма.
На листе «Перерасчет «выборка 10 000» можно скорректировать длину интервала группирования и их количество, остальные данные автоматически копируются с листа «Расчет «выборка 10 000». Строится гистограмма. Этот лист позволяет наглядно продемонстрировать, к чему ведут ошибки при вычислении длины интервала или их количества.
На листе «Генератор корреляционных таблиц 5 на 5» можно получить случайную корреляционную таблицу с результатами расчетов по ней: необходимые суммы, коэффициент корреляции, уравнения линейной регрессии. Осуществляется проверка гипотезы о значимости коэффициента корреляции, уровень значимости задается пользователем.
На листе «Расчет корреляционных таблиц» производятся вычисления полностью аналогичные вычислениям предыдущего листа, но исходные данные вводятся пользователем.
На листе «Расчет корреляционных таблиц 20 на 20» можно обрабатывать корреляционные таблицы, не превосходящие указанного в заголовке размера. Вычисляются необходимые суммы, коэффициент корреляции, уравнения линейной регрессии. Осуществляется проверка гипотезы о значимости коэффициента корреляции, уровень значимости задается пользователем.
Некоторые «несовершенные» листы, допускающие негибкость в вычислениях, оставлены после усовершенствования программы по той причине, что с ними легко работать тем, кто не гонится за универсальностью, а желает преподнести студентам сам метод вычислений.
Например, при обучении соответствующим темам курса теории вероятностей и математической статистики после разбора основных задач можно выдать студентам домашнее задание на составление программы в Excel, которая помогла бы решить большинство задач рассмотренных на занятии. Примеры составления и работы такой программы преподаватель может разобрать на конкретной задаче. Компьютер есть у многих студентов, но компьютерный класс (идеальный вариант), который можно использовать для проведения лабораторных и практических занятий по теории вероятностей и математической статистике, к сожалению, имеется не во всех вузах.
Таким образом, преподаватель, располагая компьютером и подобной программой, сможет продуктивнее выполнять подготовку к практическим занятиям по теории вероятностей и математической статистике. Например, автор использовал данную программу для написания учебного пособия по математической статистике, подготовки задач типового расчета, подбора «хороших» ответов в задачах для самостоятельного решения, при проверке задач контрольных работ заочников. Студенты же, умея пользоваться этой или аналогичной (возможно собственноручно составленной) программой, смогут осознаннее усваивать материал курса, не обременяя себя, где это возможно громоздкими вычислениями, разовьют логическое и алгоритмическое мышление, повысят компьютерную грамотность при работе с офисными программами.







