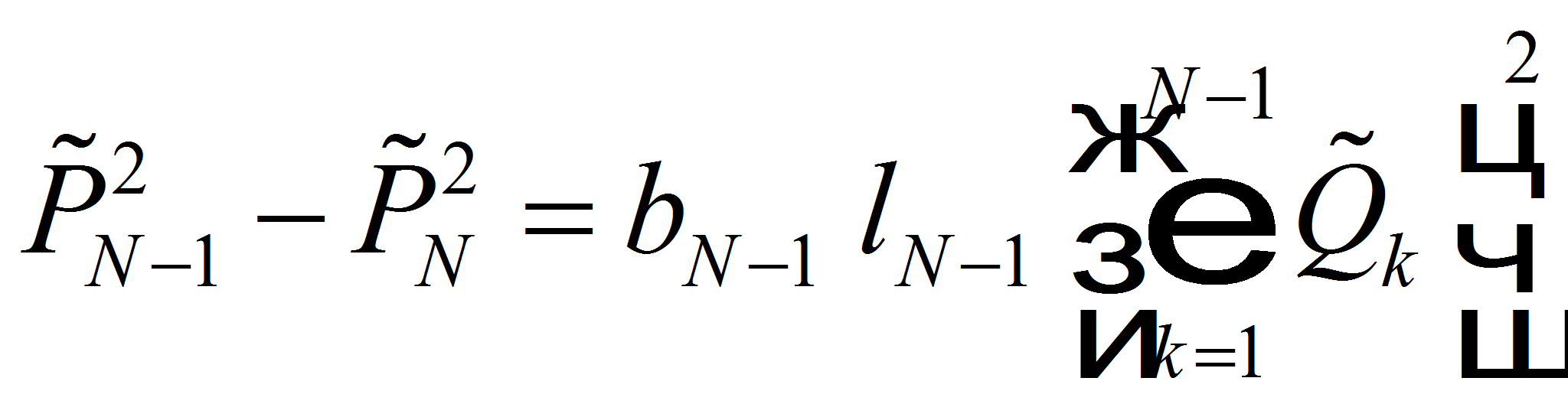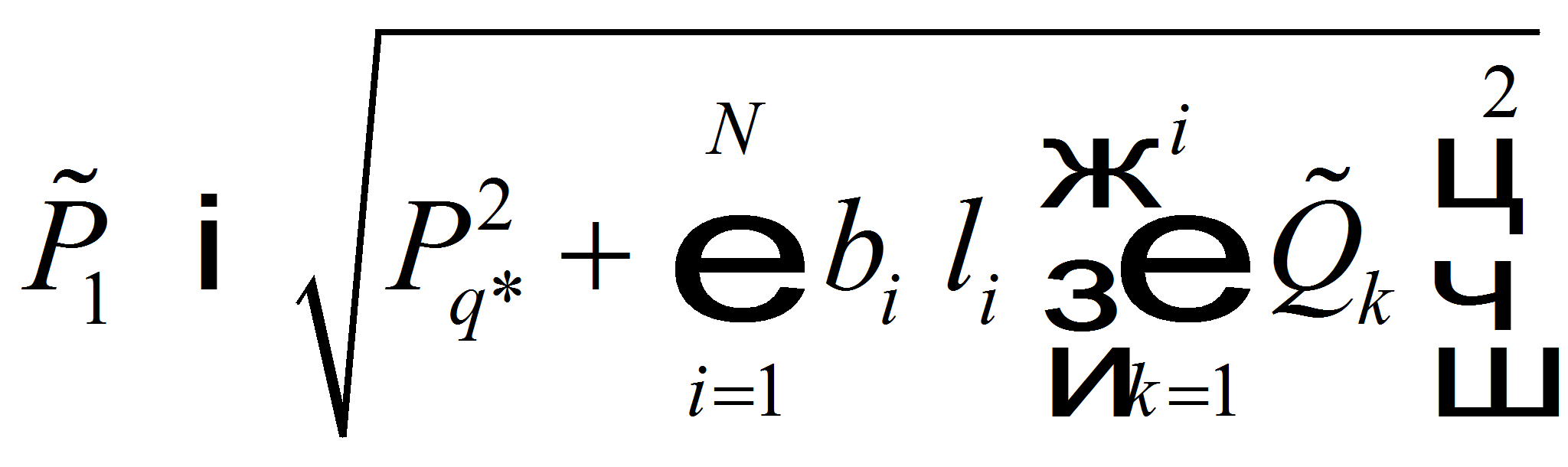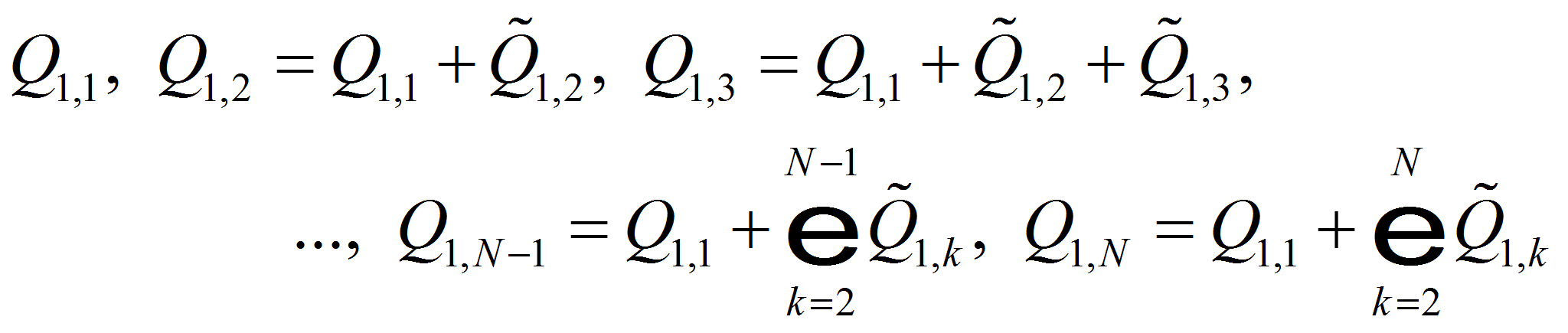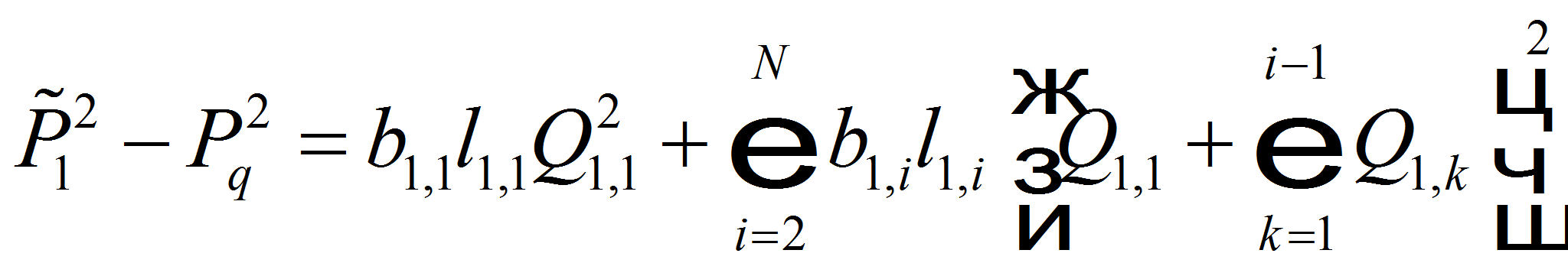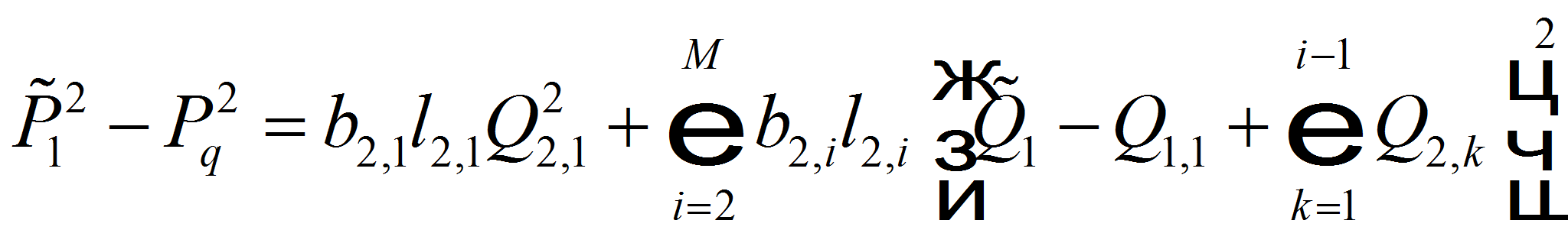В статье представлены рекомендации по гидравлическому расчету лучевой и кольцевой сети с более двумя подводами, где необходимо учитывать два типа нештатных ситуаций (когда потенциальная энергия давления подводов недостаточна для обеспечения наименьшего допустимого давления в точках отбора – нехватка энергии, и когда происходит «давка» подвода с меньшим давлением) и предлагаются пути устранения этих нештатных ситуаций.
Ключевые слова: Лучевая и кольцевая структура сети газопроводов; штатная и нештатная ситуации; узел подвода; узел отбора; гидравлика.
Рассматривая задачи и результаты расчета аварийных ситуаций видно, что из-за выхода из строя отдельного участка, кольцо разрывается и образуется сеть лучевой структуры. При отсутствии дополнительных подводов и компрессорных станций лучевая сеть характеризуется падением значения статического давления в направлении движения газа. При наличии более одного подвода в кольцевой сети необходимо соблюдать аналогичную черту организации сети с некоторыми дополнительными ограничениями.
Ниже представим материалы, которые демонстрируют подобные ограничения.
Задача 1. Рассмотрим случай, когда скважины,
в количестве
,
последовательно подключены в единую сеть с лучевой структурой.
Для этого случая принимаем следующую нумерацию
скважин и участков в цепи: 1-я скважина
1-я дуга
2-я скважина
2-я дуга
…
-я
скважина
-я
дуга
узел отбора. При этом дуги заданы показателями
,
а скважины заданы давлениями
и дебитами
.
Сомнение не вызывает следующая последовательность устьевых давлений
подключаемых скважин:
,
где
- давление на узле отбора.
С учетом участкового расхода
,
показателя
и длины
для 1-й дуги должно выполняться условие (на наши статьи}
.
Если значение левой части данного равенства превосходит значения правой части равенства, то образуется «давка» 2-й скважины (нештатная ситуация 1-го типа). Если же значение правой части данного равенства превосходит значения левой части равенства, то данный перепад квадрата давления не достаточен для преодоления силы сопротивления трения участка (нештатная ситуация 2-го типа). Проще говоря, в последнем случае газ 1-й скважины не доходит до узла подключения 2-й скважины.
При строгом выполнении условия для 1-го участка
дебит 2-й скважины поступает в сеть и расход газа на 2-м участке
равняется сумме
.
Затратив часть своей энергии на преодоление силы сопротивления 2-го
участка, в конце этого участка газ имеет статическое давление
и между давлениями 2-го и 3-го узлов установится связь
.
Не соблюдение данного условия приводит к нештатным ситуациям 1-го и 2-го типов и т.д.
Аналогично устанавливается связь между давлениями в
узлах подключения
-й
и
-й
скважин
.
При известном значении давления
в узле подключения последней скважины значение давления в узле отбора
определяется из равенства
.
Суммируя полученные равенства для перепада квадрата давлений по всем участкам, получим зависимость между устьевым давлением 1-й скважины и давлением в узле отбора
.
Если задана нижняя граница допустимого значения давления
в узле отбора, то для устьевого давления 1-й скважины налагается
условие
.
Задача 2. В качестве примера приложения приведенных выше суждений и формул из Задачи 1 рассмотрим задачу о кольцевом коллекторе с ограниченным числом узлов подвода и одним узлом отбора.
Кольцевой коллектор разделим на две цепочки скважин
(
),
каждая из которых начинается из узла с наибольшим давлением
среди узлов сети и произвольным дебитом
.
Общий расход данного узла распределяется между 1-м и 2-м цепочками по
и
:
.
Здесь
составляет участковый расход газа 1-й дуги 1-й цепочки.
Гидравлический показатель этого участка определен через коэффициент
,
а длина –
.
Участок заканчивается узлом подключения 2-й скважины 1-й цепочки с
показателями
и
.
Следующий участок 1-й цепочки имеет показатели
и
.
Участок заканчивается узлом подключения 3-й скважины 1-й цепочки с
показателями
и
.
И т.д. Последний участок 1-й цепочки начинается с точки подключения
-й
скважины с показателями
и
.
Он имеет показатели
,
и заканчивается узлом отбора газа, где устанавливается давление
отбора
.
Участковый расход газа 1-й дуги 2-й цепочки равен
.
Участки 2-й цепочки определены показателями
и
,
где
.
Подводы в узлах 2-й цепочки заданы давлениями
и дебитами
при
.
Цепочка заканчивается на узле отбора, где давление имеет значение
.
Поскольку течение газа должно быть направлено от узла с наибольшим давлением в сторону узла с наименьшим давлением, т.е. до узла отбора газа, то для давлений должно имеет место следующие последовательности
и
.
Чтобы вычислить значения давлений в узлах подвода необходимо знать участковые расходы.
С учетом предположенного нами значения расхода
1-го участка 1-й цепочки участковые расходы этой цепочки составляют
последовательность
.
Участковые расходы второй цепочки, с учетом распределения дебита 1-й скважины между цепочками, составляют
Согласно значениям участковых расходов составим уравнения для квадратов давления в узлах 1-й и 2-й цепочек. Почленное суммирование их позволяет получить взаимосвязь между давлениями 1-го и последнего узлов 1-й цепочки
и 2-й цепочки
.
Из свойства транзитивности равенств следует уравнение
Данное уравнение приводится к квадратному уравнению относительно
расхода 1-го участка 1-й цепочки
.
Решение и анализ полученного квадратного уравнения не составляет
труда. Положительность расхода газа на первых участках цепочек (
)
и строгое выполнение условий для перепада квадратов давления на
первых участках цепочек обеспечивают единственность и существование
решения уравнения.
После того, как найдено значение
,
сначала вычисляются значения участковых расходов в цепочках, а затем
узловые давления.
Как видно из представленного материала, при решении
Задачи 2, в отличие от случая кольцевого газопровода с одним подводом
и
отборами, узел с наименьшим давлением и направление потока в участках
заранее известны и отпадает необходимость поиска узла с наименьшим
давлением. Только необходимо строгое выполнение условий для перепадов
квадратов давлений в зависимости от участковых расходов, иначе
придется анализировать причины образования нештатной ситуации 1-го
или 2-го типа.
Задача 3. При произвольном числе
узлов подвода и узлов отбора между ними необходимо организовать с
цепочек и выделить варианты штатной и нештатных ситуаций с помощью
проверки энергетического баланса на каждой из цепочек.
Положим, что в
-й
узел подвода имеет наибольшее давление
среди узлов подвода. Поскольку с удалением от этого узла давление
убивает. Данный факт указывает направление потока: подводимого данным
узлом газа распределяется между двумя направлениями – по ходу
часовой стрелки и против него.
Если
и
,
то примкнувшие к узлу цепочки имеют внутренние узлы с наименьшими в
своей цепочке узловыми давлениями. Реализация способа пошагового
поиска
в зависимости от
позволяет получить решение задачи, соответствующее внутренней точке
-ой
цепочки, так как
или его часть расходуется между первыми несколькими отборами.
Аналогичное утверждение применимо и для
-й
цепочки.
Если
и
,
то возможен вариант, когда в
-й
цепочке наименьшее узловое давление достигается на границе – на
узле
-го
подвода. При этом
-й
подвод может оказаться наименьшим узловыми давлением для цепочки и
т.д. Но эти варианты не составляют помеху для дальнейшего расчета,
так как известно значение
,
и этого достаточно для последовательного определения участковых
расходов. По расходам определяются направления потока на участках и
узловые давления.
Анализируем случай, когда
.
Если при этом выполняется условие
,
задача решается просто – применяется пошаговый метод поиска
,
описанный выше. Если в рамках точности машинных округлений выполнено
условие
,
то в узле
-го
подвода достигается наименьшее давление цепочки тем, что на 1-м
участке следующей цепочки расход равняется интенсивностью данного
подвода. Если же
,
возникает более сложный вариант поиска, требующий привлечения
и последующих узлов отбора. Теперь в квадратных уравнениях будут
дополнительно фигурировать также квадраты давлений
и
го
подводов. И т.д. При этом достоверность решения проверяется с
расширенными за счет вновь привлеченных данных первым и вторым
условиями.
Решение задачи при наибольшем значении давления в
сети, равном
,
существует, так как утверждение локального максимума давления
равносильно утверждению о том, что хотя бы в одном участке кольцевой
цепи поток газа имеет противоположное направление относительно потока
на других участках. И этим мы доказали, что задача имеет решение и
его можно найти с привлечением способа дискретно-непрерывного поиска.
Можно ли доказать аналогичное утверждение, если наибольшее значение давления достигается сразу двумя и более узлами подвода? Ответ – да.
Поскольку давление является непрерывной функцией по всей длине кольцевой сети и имеет, в этом случае, несколько локальных максимумов, то в малой окрестности каждого локального максимума давление убывает. Соответственно, в примыкающих к данному узлу участках движения газа имеют разные направления и для каждого из них можно применять суждения, приведенного для случая единичного локального максимума. Единственным препятствием может быть случай, когда цепочка между двумя локальными максимумами не имеет узлов отбора. Интенсивности подводов в этих узлах составляют расходы абсолютных значений соответствующих участков и счет можно продолжать.
В целом, случай отсутствия в цепочке узлов отбора является самой легко решаемой среди анализируемых. В этом случае участковый расход в данной цепочке кольца определяется однозначно по формуле
.
При известном значении
значения и направления расхода на одном из участков, можно продолжать
расчет расходов и давлений до конечного вида.
Совместимость исходных данных задач проверяется согласованностью между вновь вычисленными и заданными значениями давления в подводах в рамках выполнения точности машинного округления. А тип нештатной ситуации определяется разностью квадратов заданного и вновь вычисленного значений давлений в подводах, а также возникновения отрицательного значения квадрата в отдельном узле.
- Литература:
Коротаев Ю.П., Ширковский А.И. Добыча, транспорт и подземное хранение газа. - М.: Недра, 1997. – 487 с.
Сеннова Е.В., Сидлер В.Г. Математическое моделирование и оптимизация развивающихся теплоснабжающих систем. – Новосибирск: Наука. – 1987. – 222 с.
Трубопроводный транспорт нефти и газа / Под общ. ред. В.А. Юфина. – М.: Недра,1978. – 407 c.
Хужаев И.К., Юлдашев Б.Э., Куканова М.А. Эффективность кольцевой структуры газопровода и алгоритм расчета ее гидродинамических показателей // Вопросы вычислительной и прикладной математики. Аналитические методы и вычислительные алгоритмы решения задач математической физики. Ташкент. 2011. Вып. 126. С.132-143.
Юлдашев Б.Э., Хужаев И.К., Куканова М.А. Гидравлический расчет «давки» в кольцевом газопроводе с двумя подводами и с одним отбором// Сочи, «European Researcher». № 1(16), 2012. - С.30-36.
