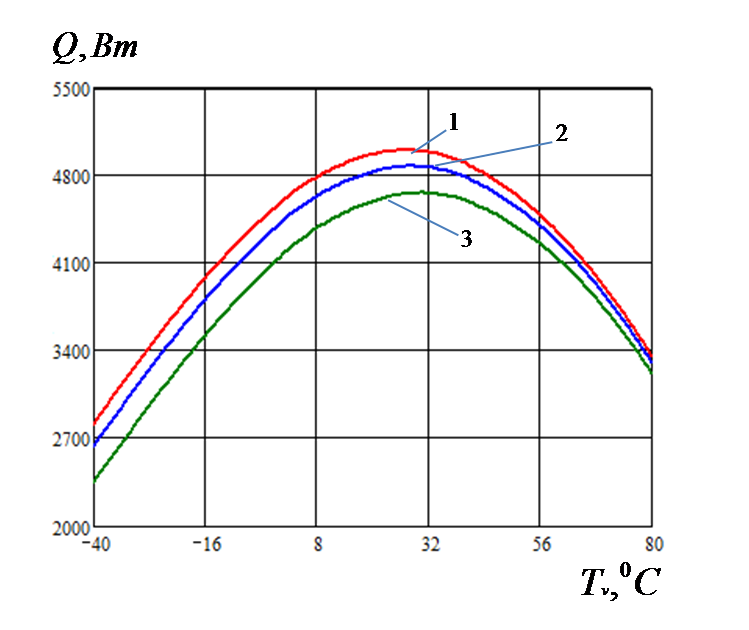
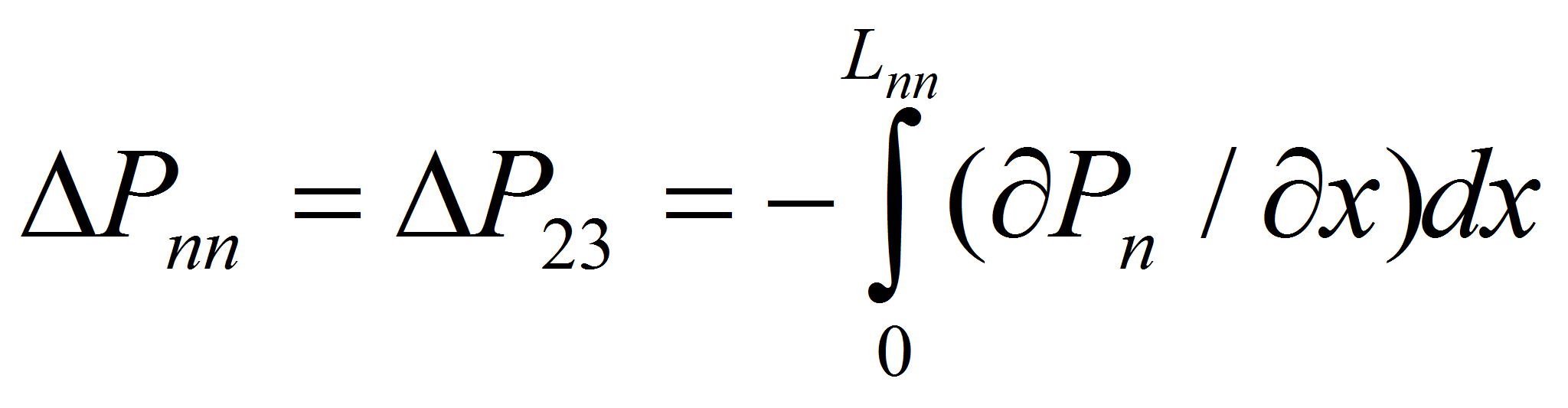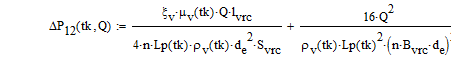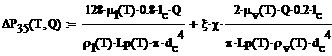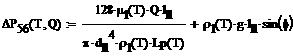- Введение. История
интенсивного развития высокоэффективных теплопередающих устройств,
которые получили название «тепловая труба», насчитывает
уже более 40 лет, если считать началом их существования 2 декабря
1963 года, когда на имя американского физика Джорджа Гровера из
Лос-Аламосской национальной лаборатории был зарегистрирован патент №
3229759 под названием «конденсационно-испарительное
теплопередающее устройство». С тех пор ученые нашли множество
отраслей, в которых использование тепловых труб является актуальным.
Это связано с тем, что выделение тепла является одним из наиболее
распространенных процессов, которые сопровождают работу различных
технических объектов. В одних ситуациях это тепло приводит к
нарушению тепловых режимов, и его необходимо отводить. В других –
тепло подводят к объекту, тем самым обеспечивая его
работоспособность [1]. Тепловые трубы незаменимы для систем
терморегулирования космических аппаратов. Также они получили широкое
применение в надземной технике для охлаждения теплонапряженных
компонентов различных электронных устройств и компьютерной техники,
в атомной энергетике, в промышленных теплообменниках и системах
кондиционирования, в медицинской технике, пищевой промышленности и
многих других.
- Тем не менее, современные технологии выдвигают новые требования, с которыми конструкция обычных тепловых труб не может справиться. Например, ограничением является их довольно высокая чувствительность к изменению положения в поле силы тяжести. Небольшой наклон, в результате которого зона испарения оказывается выше зоны конденсации, приводит к снижению эффективности тепловых труб.
- Необходимо было создать устройство, которое обладало всеми основными достоинствами обычных тепловых труб, и в то же время было свободно от их недостатков. Такое устройство было создано и получило название контурная тепловая труба (КТТ).
- Целью данной работы является произвести расчет максимальной теплопередающей способности аммиачной контурной тепловой трубы с длиной теплопереноса 1 метр.
- Для достижения поставленной цели необходимо решить следующий ряд задач:
- 1) изучить научную литературу по теплопередающим устройствам с капиллярной прокачкой теплоносителя;
- 2) ознакомиться с методикой расчета рабочих характеристик КТТ;
- 3) разработать алгоритм решения задачи по расчету максимальной теплопередающей способности КТТ (
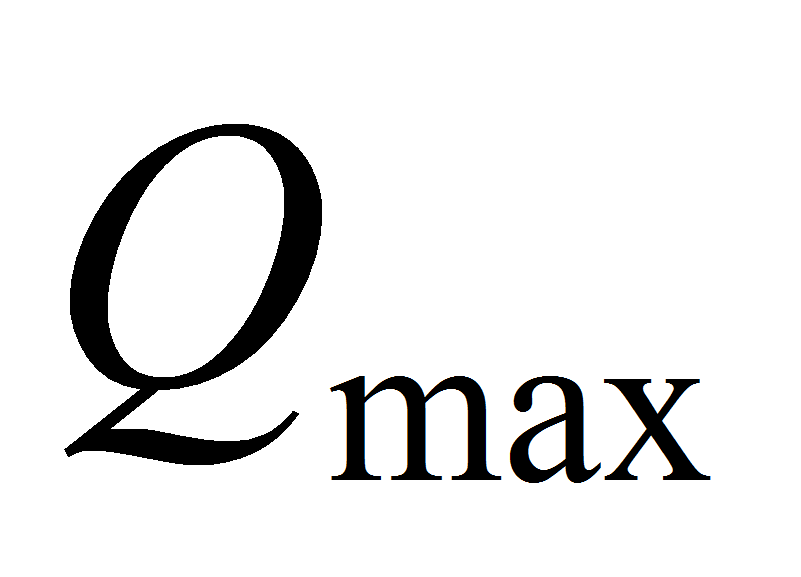 );
);- 4) создать программу в пакете MathCAD для расчета максимальной теплопередающей способности КТТ;
- 5) провести анализ полученных результатов.
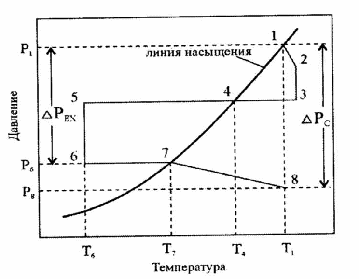
- Условия работоспособности контурных тепловых труб. Сформулированная концепция контурной тепловой трубы может быть реализована при выполнении ряда условий. На рис. 1 схематично показан рабочий цикл теплоносителя в КТТ в координатах «температура, давление».
- Тем не менее, современные технологии выдвигают новые требования, с которыми конструкция обычных тепловых труб не может справиться. Например, ограничением является их довольно высокая чувствительность к изменению положения в поле силы тяжести. Небольшой наклон, в результате которого зона испарения оказывается выше зоны конденсации, приводит к снижению эффективности тепловых труб.
Рис. 1. Диаграмма рабочего цикла контурной тепловой трубы
-
Точка 1, находящаяся на
линии насыщения, соответствует параметрам пара над испаряющей
поверхностью мениска. Участок 1-2 соответствует движению пара с этой
поверхности в паропровод. Потери давления здесь обусловлены, в
первую очередь, гидравлическим сопротивлением пароотводных каналов.
Кроме того, на этом участке в общем случае повышается температура
пара вследствие его теплового контакта с корпусом испарителя.
Паропровод в большинстве случаев можно считать адиабатическим, а
движение пара в нем – изотермическим (прямая 2-3). Потери
давления в конденсаторе (прямая 3-5), как правило, пренебрежимо малы
по сравнению с капиллярным давлением. Теплоноситель здесь переходит
из паровой фазы в жидкую, и на теплообменном участке 4-5
переохлаждается. Дальнейший транспорт теплоносителя по
конденсатопроводу также можно полагать изотермическим и
сопровождающимся только потерей давления (участок 5-6). В результате
в компенсационную полость поступает переохлажденная жидкость с
давлением
 .
В то же время, в компенсационную полость проникает часть подводимого
к испарителю теплового потока, в результате чего переохлажденный
конденсат прогревается до температуры, соответствующей по линии
насыщения давлению
.
В то же время, в компенсационную полость проникает часть подводимого
к испарителю теплового потока, в результате чего переохлажденный
конденсат прогревается до температуры, соответствующей по линии
насыщения давлению
 (прямая 6-7). Это соответствует тому, что над границей раздела фаз в
компенсационной полости находится насыщенный пар. Участок 7-8
соответствует фильтрации теплоносителя из компенсационной полости к
поверхности парообразования через капиллярную структуру. На этом
участке, с одной стороны, имеет место падение давления жидкости, а с
другой – повышение ее температуры. Таким образом, точка 8 на
рис. 4 соответствует состоянию теплоносителя в жидкой фазе вблизи
испаряющего мениска [2, с.15].
(прямая 6-7). Это соответствует тому, что над границей раздела фаз в
компенсационной полости находится насыщенный пар. Участок 7-8
соответствует фильтрации теплоносителя из компенсационной полости к
поверхности парообразования через капиллярную структуру. На этом
участке, с одной стороны, имеет место падение давления жидкости, а с
другой – повышение ее температуры. Таким образом, точка 8 на
рис. 4 соответствует состоянию теплоносителя в жидкой фазе вблизи
испаряющего мениска [2, с.15].- Как следует из приведенной диаграммы, полный перепад давления равен сумме потерь давления на участках КТТ:
-
С другой стороны,
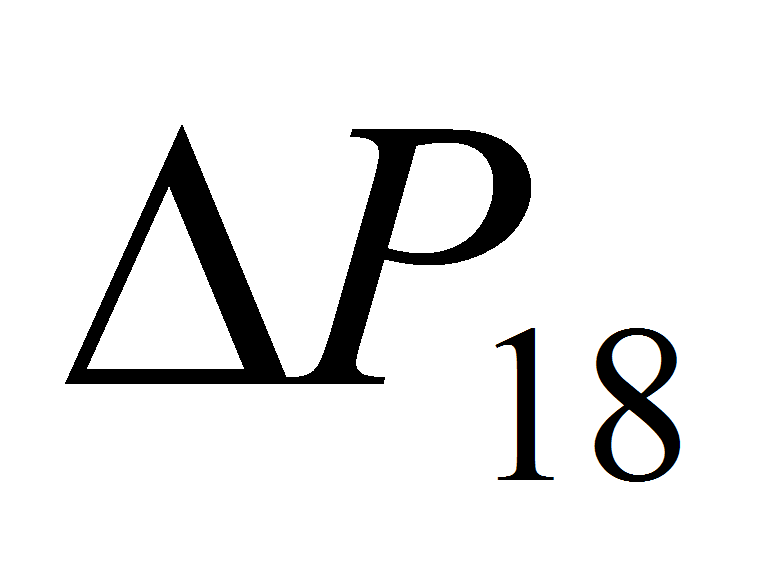 есть капиллярное давление
есть капиллярное давление
 .
Таким образом, первое условие работоспособности тепловых труб
контурного типа может быть сформулировано следующим образом:
.
Таким образом, первое условие работоспособности тепловых труб
контурного типа может быть сформулировано следующим образом:
-
Оно утверждает, что потери
давления в тепловой трубе компенсируются капиллярным давлением и
поэтому не могут превышать максимального капиллярного давления
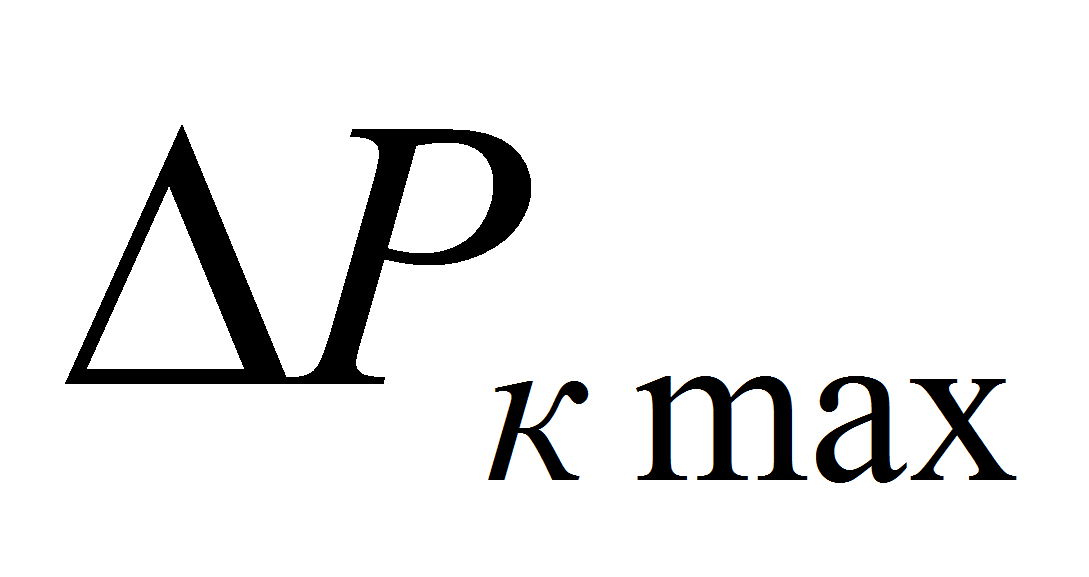 :
:
-
Это условие является общим
для всех типов тепловых труб, использующих капиллярный механизм
транспортировки конденсата. Его необходимо учитывать при выборе
геометрических параметров транспортных участков тепловой трубы и при
выборе теплоносителя.
- Второе условие работоспособности характерно для тепловых труб контурного типа и связывает перепад температуры пара на поверхности парообразования и в компенсационной полости
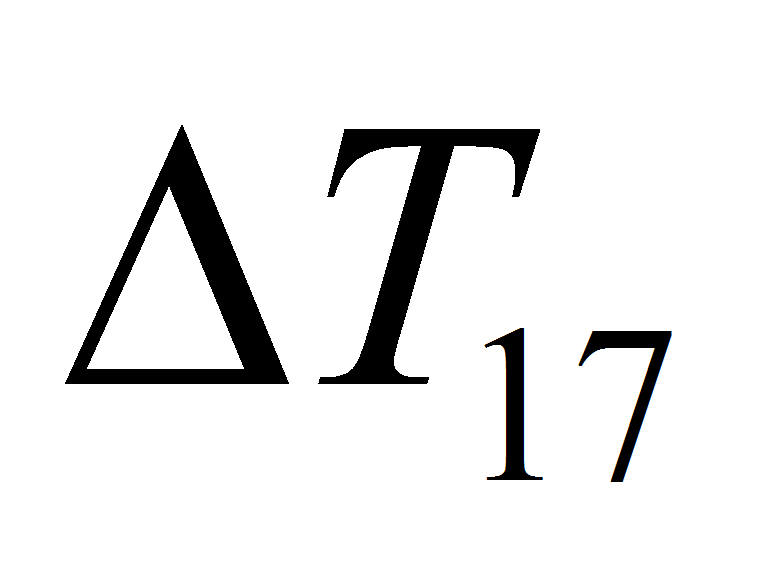 с соответствующим перепадом давления
с соответствующим перепадом давления
 .
Перепад давления
.
Перепад давления
 складывается из следующих составляющих:
складывается из следующих составляющих:
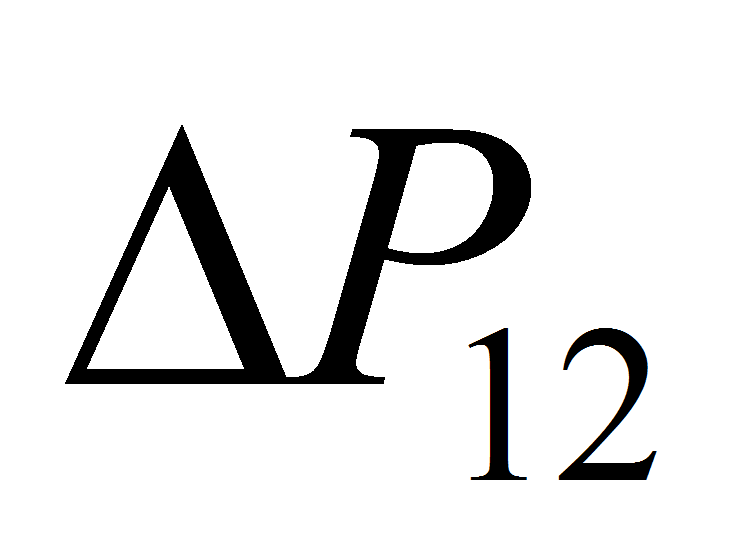 ,
,
 ,
,
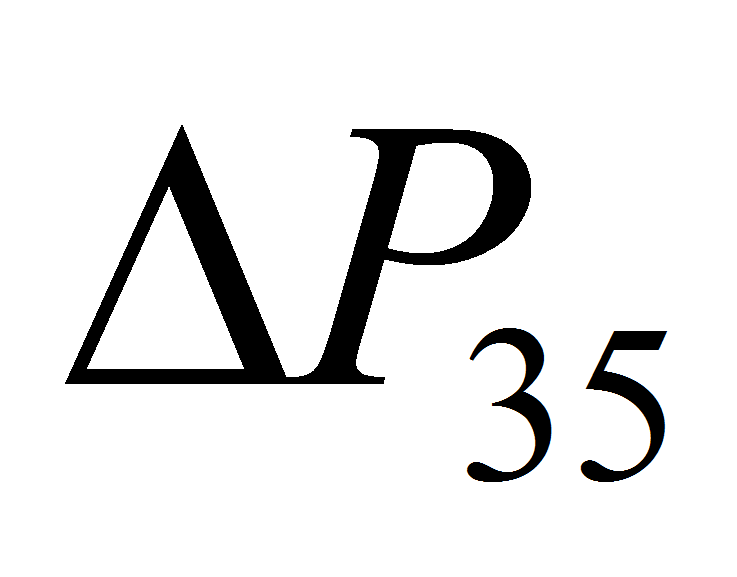 и
и
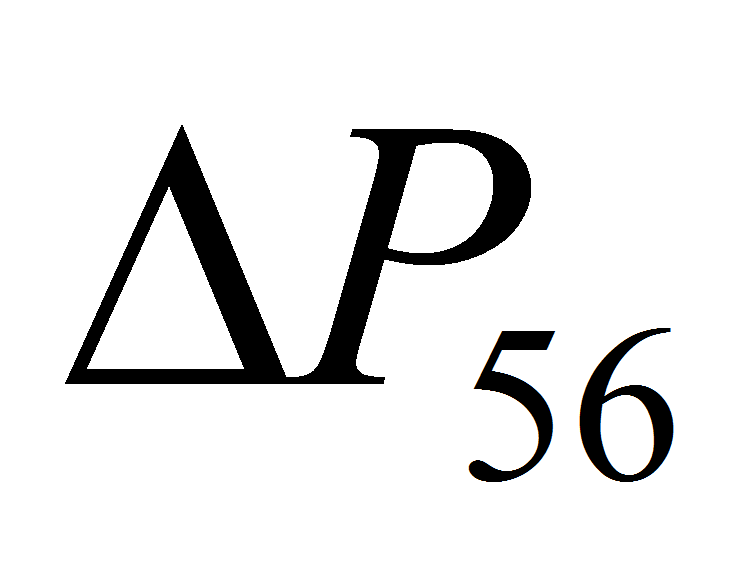 .
Так как пар над испаряющими менисками и в компенсационной полости
предполагается насыщенным, данное условие записывается следующим
образом:
.
Так как пар над испаряющими менисками и в компенсационной полости
предполагается насыщенным, данное условие записывается следующим
образом:
- Второе условие работоспособности характерно для тепловых труб контурного типа и связывает перепад температуры пара на поверхности парообразования и в компенсационной полости
-
В качестве
 обычно
берется среднее значение между
обычно
берется среднее значение между
 и
и
 .
Величина
.
Величина
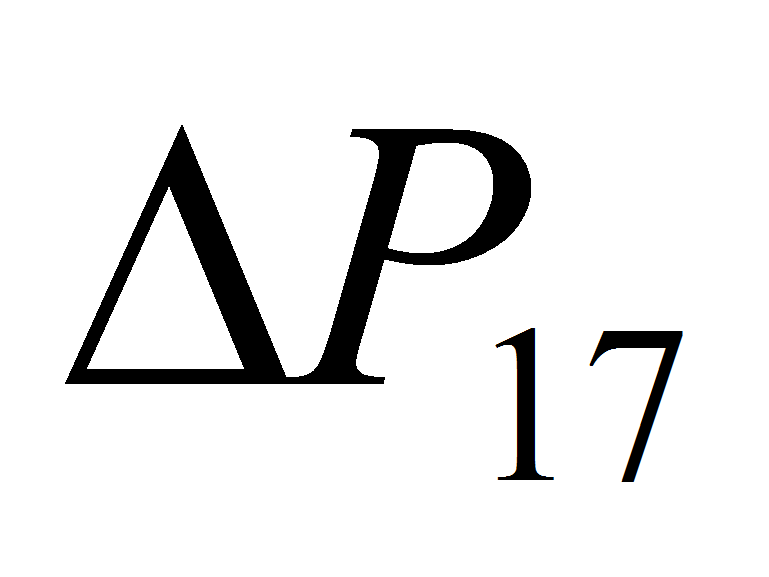 представляет собой суммарный перепад давления во внешнем,
относительно капиллярной структуры, контуре КТТ. Обозначим его
представляет собой суммарный перепад давления во внешнем,
относительно капиллярной структуры, контуре КТТ. Обозначим его
 ,
заменим
,
заменим
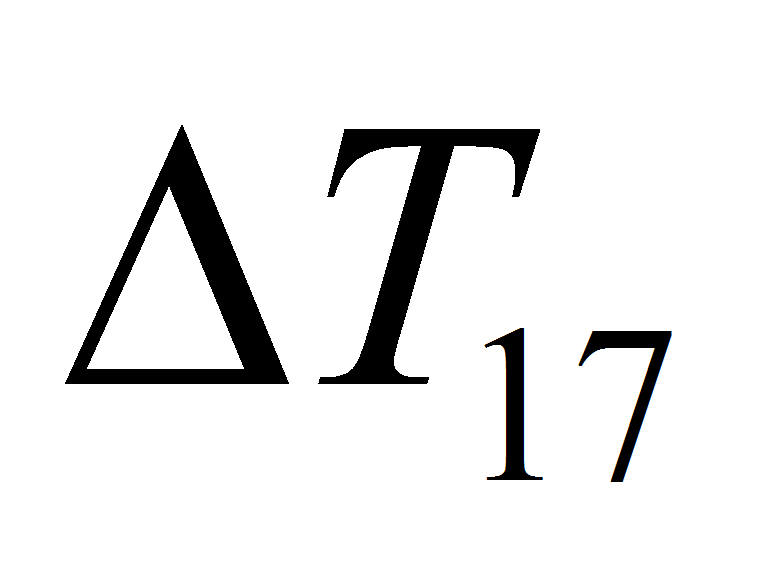 на
на
 ,
и окончательно получим запись второго условия работоспособности:
,
и окончательно получим запись второго условия работоспособности:
-
Разность температур пара в
зоне испарения и в компенсационной полости
 возникает вследствие того, что часть подводимого к испарителю
теплового потока проникает через капиллярную структуру в
компенсационную полость. В первом приближении можно полагать, что
указанная разность температур формируется между испаряющей
(наружной) и впитывающей (внутренней) поверхностями капиллярной
структуры.
возникает вследствие того, что часть подводимого к испарителю
теплового потока проникает через капиллярную структуру в
компенсационную полость. В первом приближении можно полагать, что
указанная разность температур формируется между испаряющей
(наружной) и впитывающей (внутренней) поверхностями капиллярной
структуры.- Существование второго условия позволяет в определенных пределах управлять рабочей температурой тепловых труб контурного типа, причем средства такого управления достаточно широки. Сюда относятся: выбор теплоносителя, вариация геометрических параметров транспортных зон, капиллярной структуры, испарителя, степени переохлаждения конденсата.
- Рассматриваемое условие работоспособности КТТ связывает температуру и давление пара в зоне испарения и в компенсационной плоскости. Оно, таким образом, предполагает наличие в компенсационной полости паровой фазы. То есть, компенсационная полость, частично заполнена жидким теплоносителем, а частично – паром. Для обеспечения такого частичного заполнения при переходе тепловой трубы в стационарный режим работы, необходимо соблюсти определенное соотношение между объемами ряда конструктивных элементов. Эта необходимость позволяет сформулировать третье условие работоспособности контурных тепловых труб.
- Необходимо, чтобы выталкиваемая при запуске КТТ из парового канала жидкость заполнила частично конденсатор и частично компенсационную полость. Это возможно, при выполнении условия:
- Существование второго условия позволяет в определенных пределах управлять рабочей температурой тепловых труб контурного типа, причем средства такого управления достаточно широки. Сюда относятся: выбор теплоносителя, вариация геометрических параметров транспортных зон, капиллярной структуры, испарителя, степени переохлаждения конденсата.
-
Невыполнение третьего
условия может привести к тому, что компенсационная полость окажется
целиком заполненной жидкостью, в результате чего станет невозможным
формирование необходимой поверхности конденсации, что в свою очередь
может привести к нарушению работоспособности КТТ.
- Перечисленные условия являются необходимыми и достаточными для нормальной работы тепловых труб контурного типа.
- Рабочие характеристики контурных тепловых труб. Рабочие характеристики используются для инженерного расчета контурных тепловых труб. Задача расчета КТТ может быть поставлена в двух вариантах: проверочном и конструкторском. В первом случае требуется определить такие характеристики как температура в зоне подвода тепла, рабочая температура пара, термическое сопротивление КТТ, теплопередающая способность. В случае конструкторского расчета задача состоит в определении тех или иных конструктивных параметров КТТ или условий работы, которые обеспечили бы требуемые рабочие характеристики [3, с.139]. Сюда же относятся задачи оптимизации и выбора подходящего теплоносителя. В самом общем виде расчет КТТ сводится к решению сопряженной задачи тепломассопереноса с начальными и граничными условиями, определяемыми теплоподводом и теплоотводом, конструктивными особенностями тепловой трубы, а также теплообменом с окружающей средой. На практике приходится делать допущения, которые вызваны либо спецификой процессов переноса и конструкцией КТТ, либо необходимостью упрощения для получения решения.
- Как следует из условий работоспособности КТТ (1.1-1.2), теплопередающая способность КТТ и температура зависят, в частности, от величин потерь давления теплоносителя на различных транспортных участках. Потери давления в паропроводе, ранее обозначенные как
 ,
существенно зависят от режима течения пара. Этот режим, в свою
очередь, определяется значением критерия Рейнольдса:
,
существенно зависят от режима течения пара. Этот режим, в свою
очередь, определяется значением критерия Рейнольдса: - Перечисленные условия являются необходимыми и достаточными для нормальной работы тепловых труб контурного типа.
-
причем
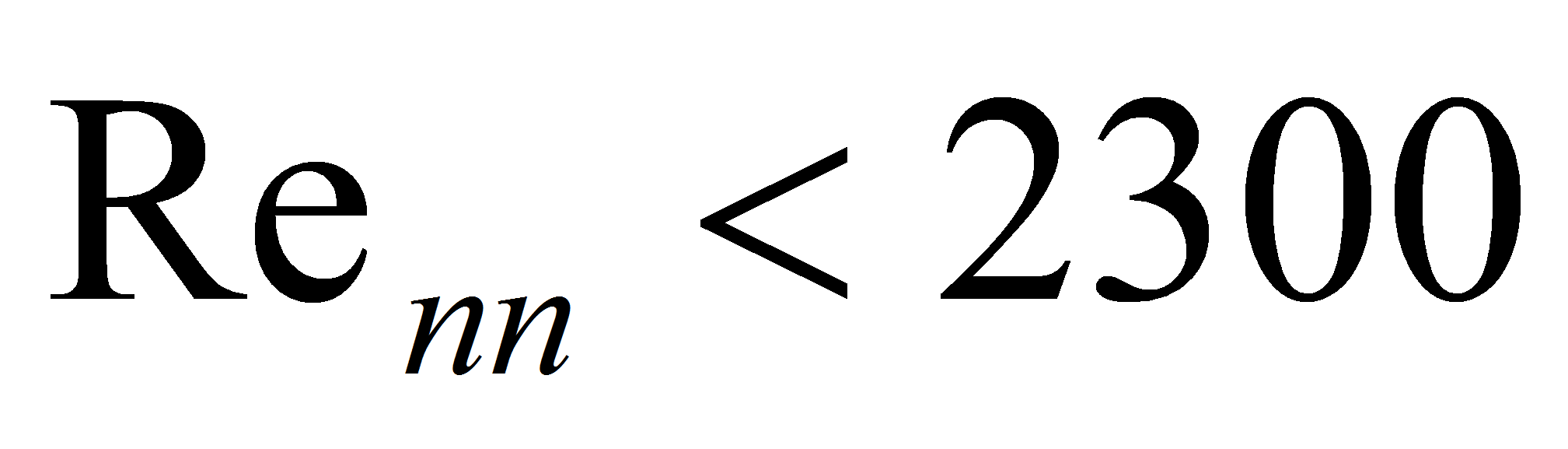 соответствует
ламинарный режим течения,
соответствует
ламинарный режим течения,
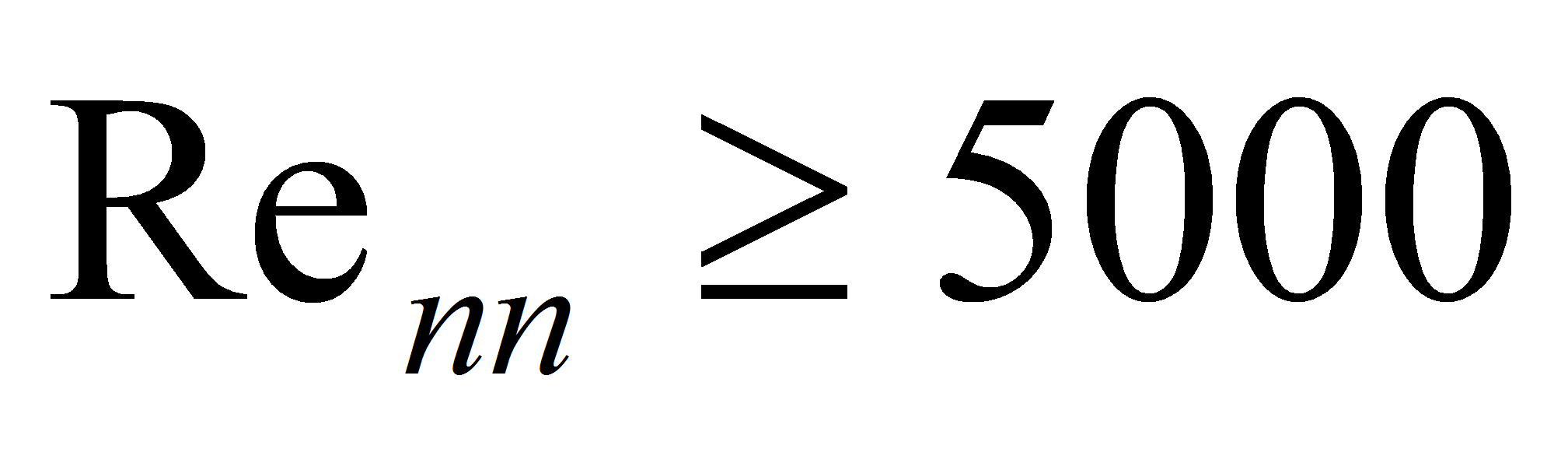 -
развитый турбулентный, а случаю
-
развитый турбулентный, а случаю
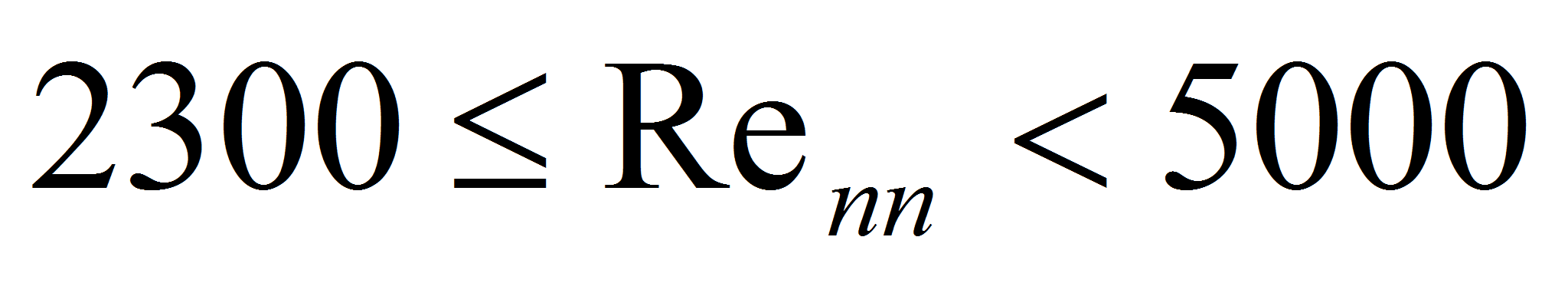 -
переходный режим.
-
переходный режим.- Обычная формула для вычисления потерь давления в паропроводе имеет вид:
- где градиент давления пара в направлении его движения в общем виде определяется:
-
Значения коэффициента
трения
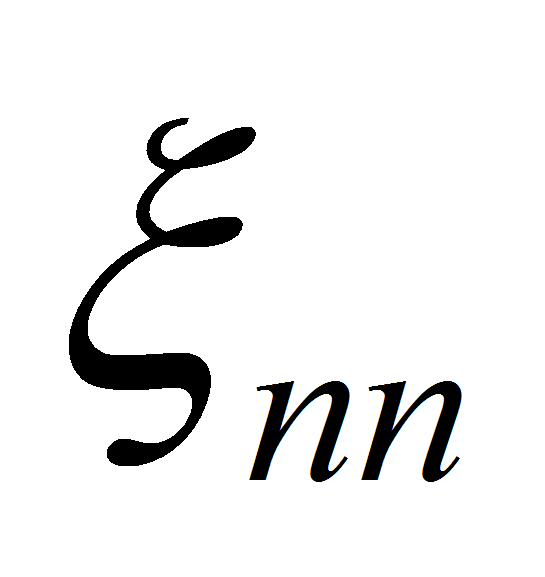 и коэффициента
и коэффициента
 ,
учитывающего эффект сжимаемости пара, взяты из справочной таблицы.
Здесь М – критерий Маха:
,
учитывающего эффект сжимаемости пара, взяты из справочной таблицы.
Здесь М – критерий Маха:
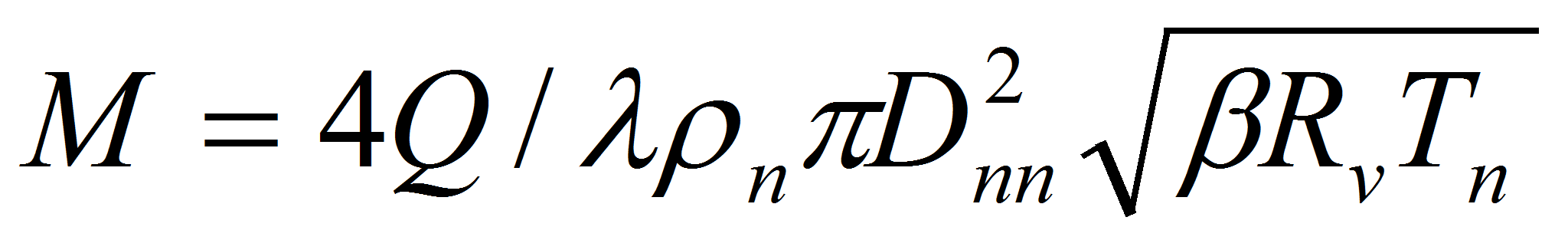 ,
а
,
а
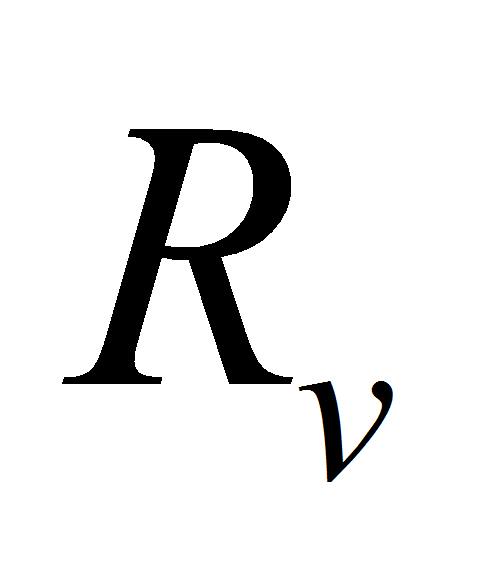 ,
,
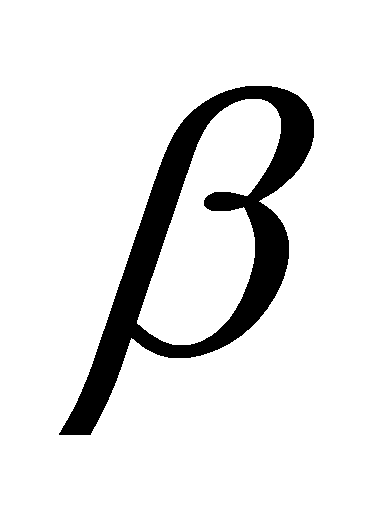 - газовая постоянная теплоносителя и показатель адиабаты
соответственно.
- газовая постоянная теплоносителя и показатель адиабаты
соответственно.- В отсутствии действия поля массовых сил, потери давления в паропроводе составляют обычно большую часть величины
 ,
поэтому в процессе расчета КТТ желательно определить значение
,
поэтому в процессе расчета КТТ желательно определить значение
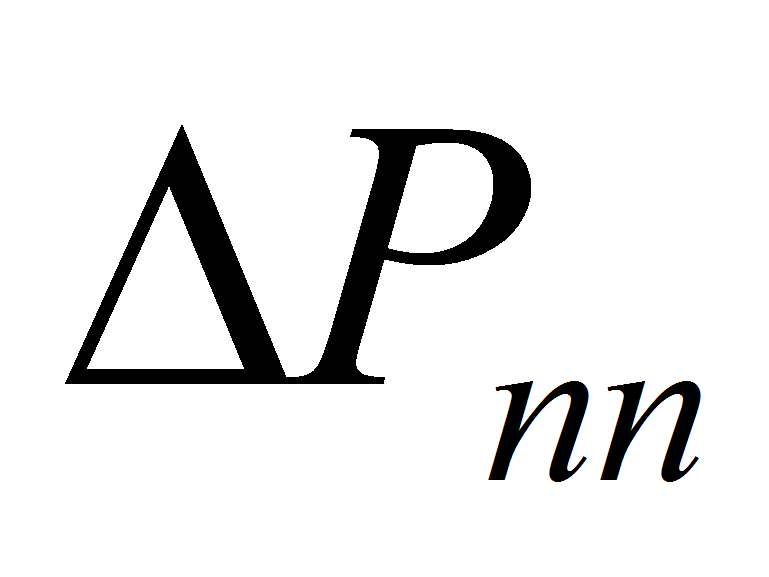 по возможности более точно.
по возможности более точно.
- Расчет потерь давления в пароотводных каналах (
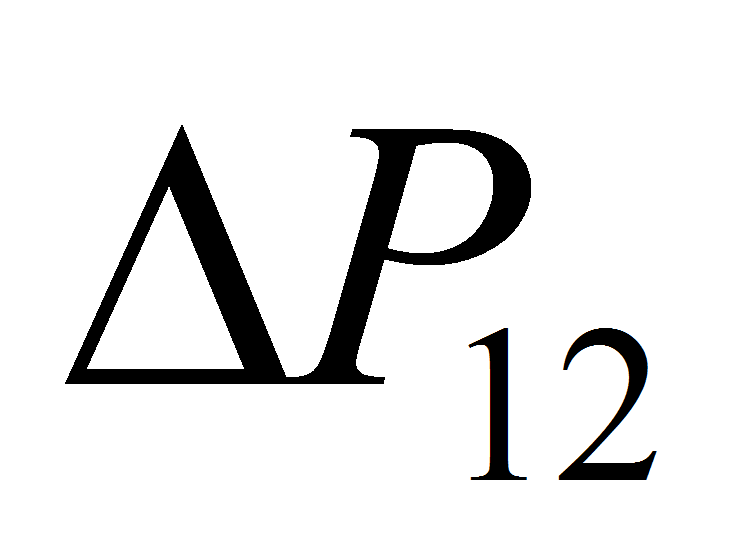 в формуле 1.1) резко осложняется наличием вдува пара, а также тем,
что сечение пароотводных каналов может иметь различную форму. В
настоящее время возможно определение потерь давления пара в
пароотводных каналах только в случае ламинарного течения, т. е. в
случае
в формуле 1.1) резко осложняется наличием вдува пара, а также тем,
что сечение пароотводных каналов может иметь различную форму. В
настоящее время возможно определение потерь давления пара в
пароотводных каналах только в случае ламинарного течения, т. е. в
случае
 .
В последнем соотношении
.
В последнем соотношении
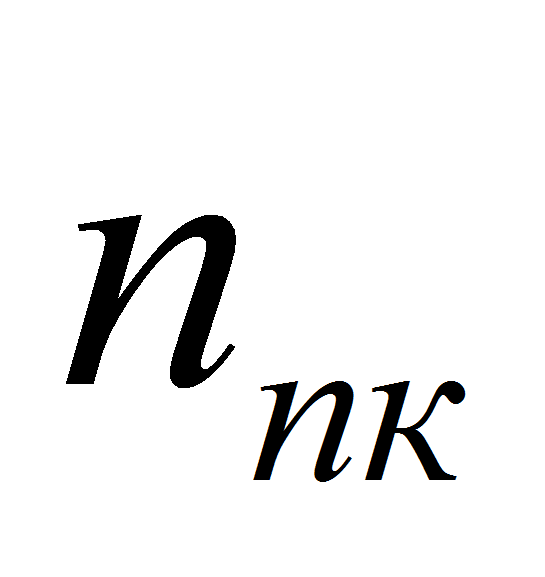 - число пароотводных каналов,
- число пароотводных каналов,
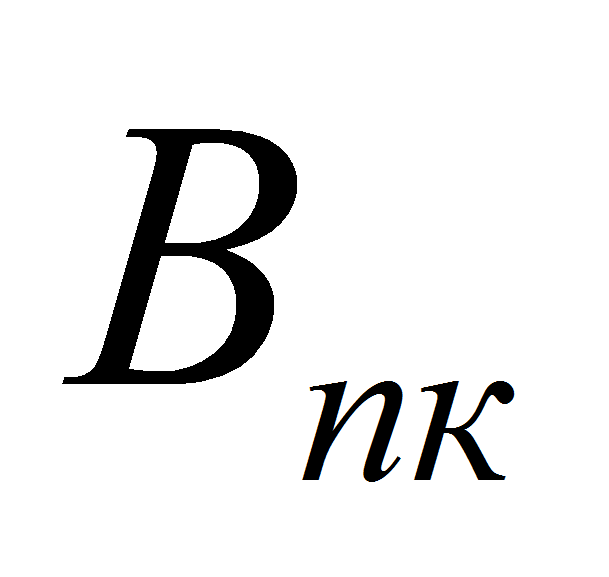 -
периметр сечения. Так как учесть влияние вдува пара на коэффициент
трения воздуха не предоставляется возможным, считается, что их
сопротивление складывается из двух составляющих: вязкостной
-
периметр сечения. Так как учесть влияние вдува пара на коэффициент
трения воздуха не предоставляется возможным, считается, что их
сопротивление складывается из двух составляющих: вязкостной
 и инерционной
и инерционной
 .
Первая из них определяется сопротивлением трения без учета вдува:
.
Первая из них определяется сопротивлением трения без учета вдува: - В отсутствии действия поля массовых сил, потери давления в паропроводе составляют обычно большую часть величины
-
где
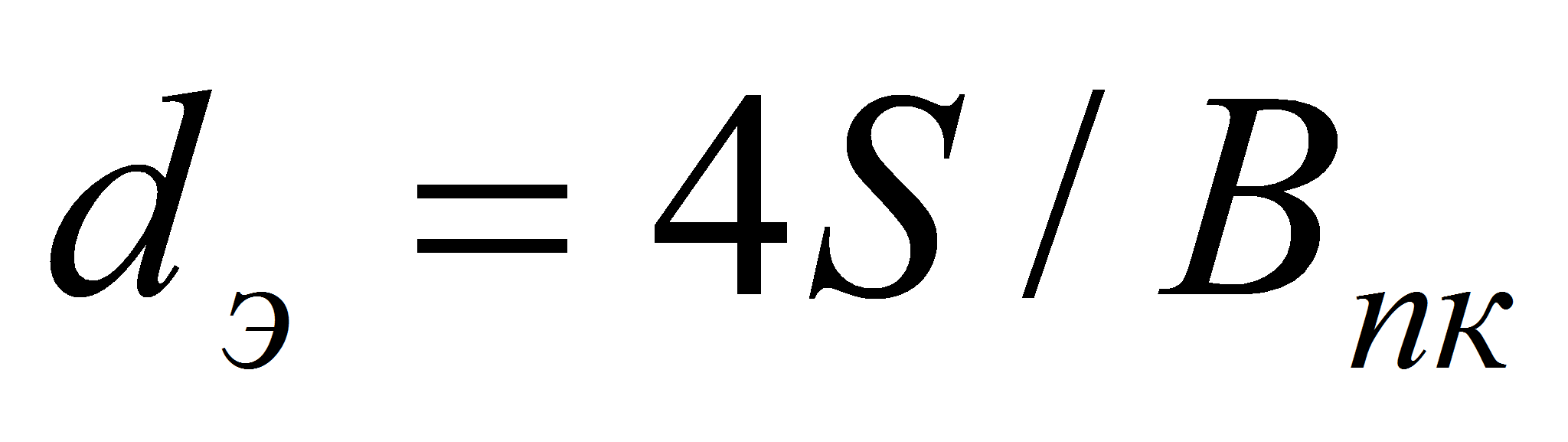 -
эквивалентный параметр,
-
эквивалентный параметр,
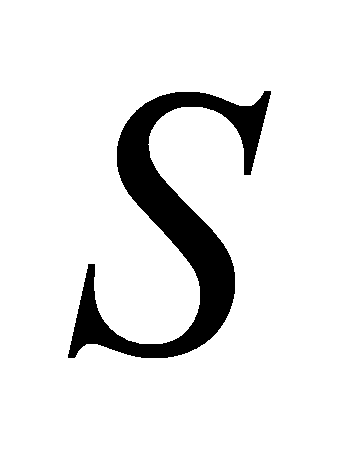 - сечение, коэффициент
- сечение, коэффициент
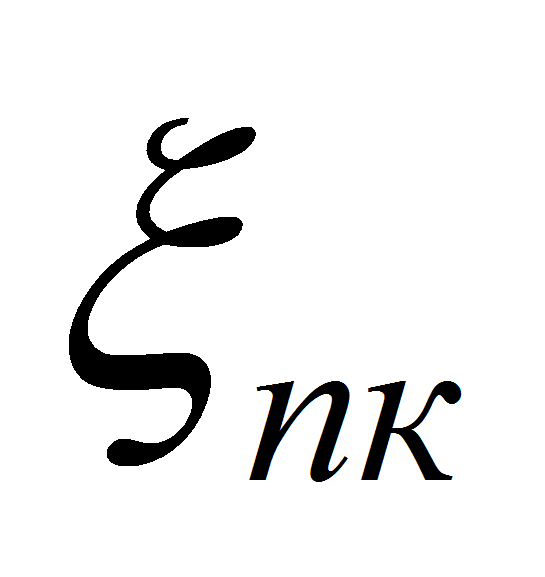 учитывает форму канала. Инерционную составляющую в первом
приближении можно определить по формуле:
учитывает форму канала. Инерционную составляющую в первом
приближении можно определить по формуле:
- Расчет потерь давления в конденсаторе невозможен без учета теплообмена с окружающей средой. При выполнении практических расчетов КТТ в настоящее время гидравлическое сопротивление конденсатора не учитывается. Гидравлическое сопротивление конденсатопровода определяется по формуле:
-
Первое слагаемое правой
части формулы определяет сопротивление трения. Эта величина, как
правило, пренебрежимо мала. Второе слагаемое учитывает
гидростатическое давление, связанное с действием гравитационного
поля.
- Потери давления в капиллярной структуре рассчитываются в приближении Дарси и для испарителей рассматриваемого типа имеют вид:
-
Тепловой аспект расчета
КТТ состоит в определении перепадов температуры на основных
теплонапряженных участках, а именно в капиллярной структуре, зонах
испарения и конденсации. Для оценки термической проводимости
капиллярной структуры удобно пользоваться безразмерным
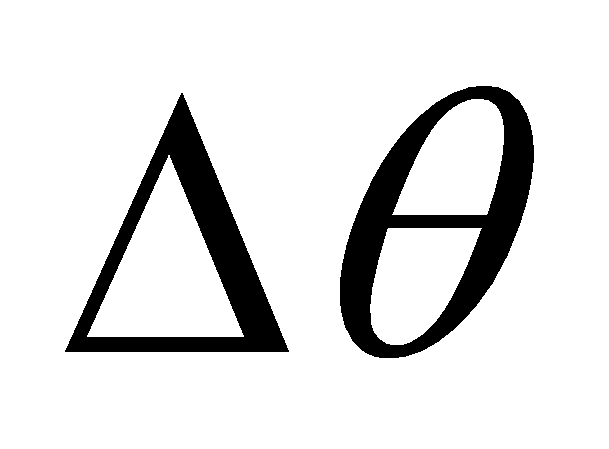 ,
который согласно формуле
,
который согласно формуле
- имеет вид:
-
где
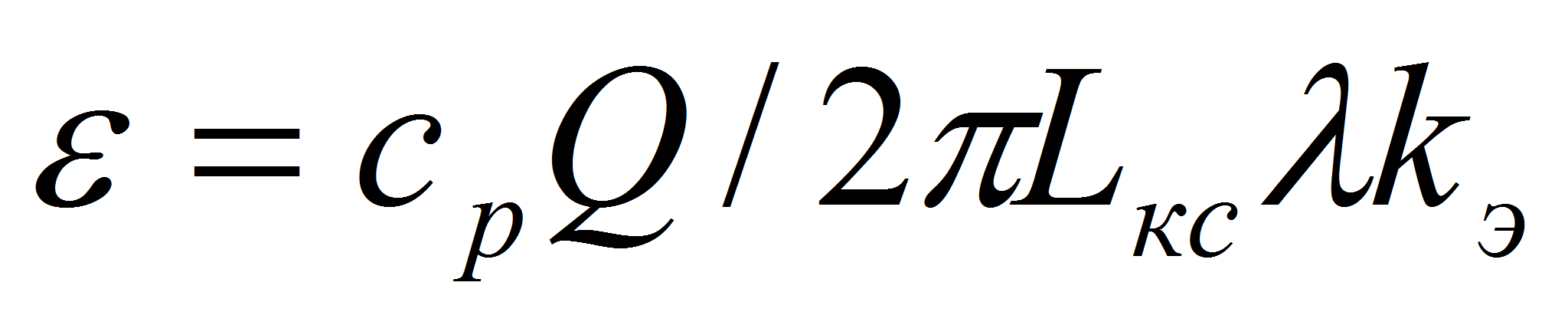 .
Формула (3.9) справедлива в случае
.
Формула (3.9) справедлива в случае
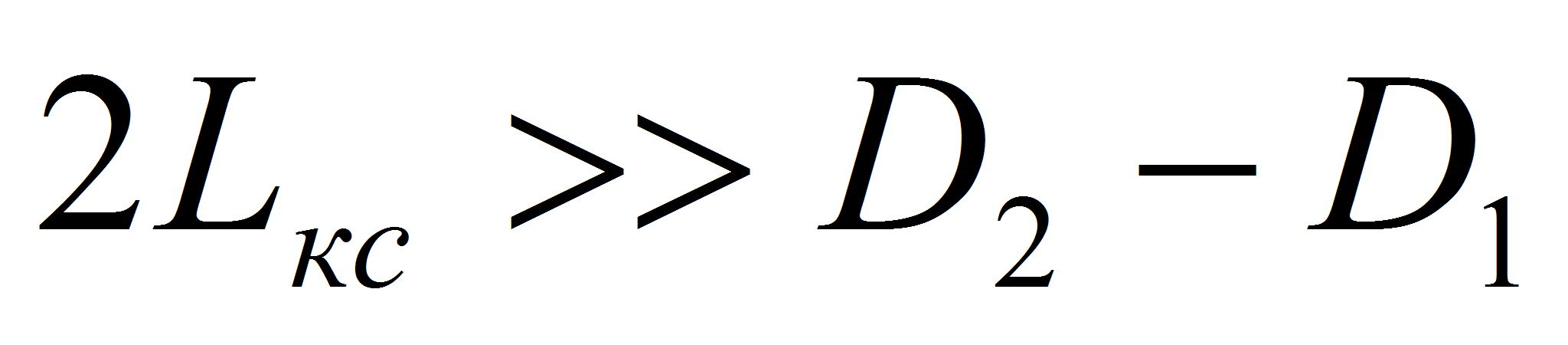 ,
то есть когда длина капиллярной структуры значительно больше ее
толщины. В реальных тепловых трубах характерные размеры капиллярных
структур таковы, что указанное соотношение соблюдается, но более
точной является функциональная зависимость:
,
то есть когда длина капиллярной структуры значительно больше ее
толщины. В реальных тепловых трубах характерные размеры капиллярных
структур таковы, что указанное соотношение соблюдается, но более
точной является функциональная зависимость:
-
где
 - безразмерный критерий Пекле.
- безразмерный критерий Пекле.
- Расчет максимальной теплопередающей способности аммиачной контурной тепловой трубы с длиной теплопереноса 1 метр.
Исходные данные
-
Параметры капиллярной
структуры:
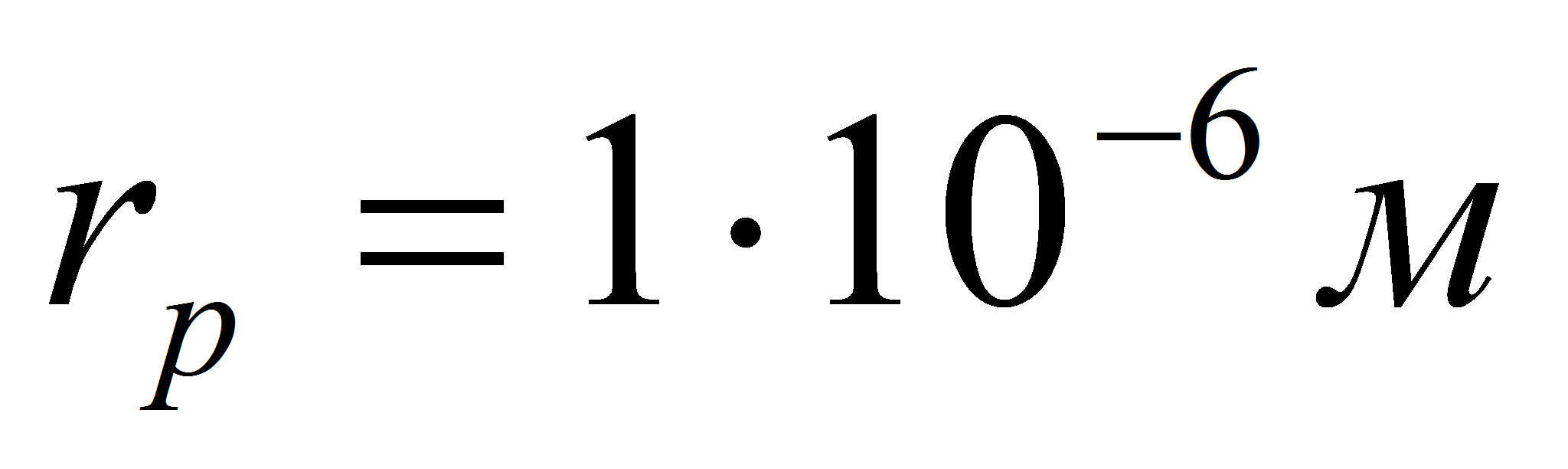 ,
,
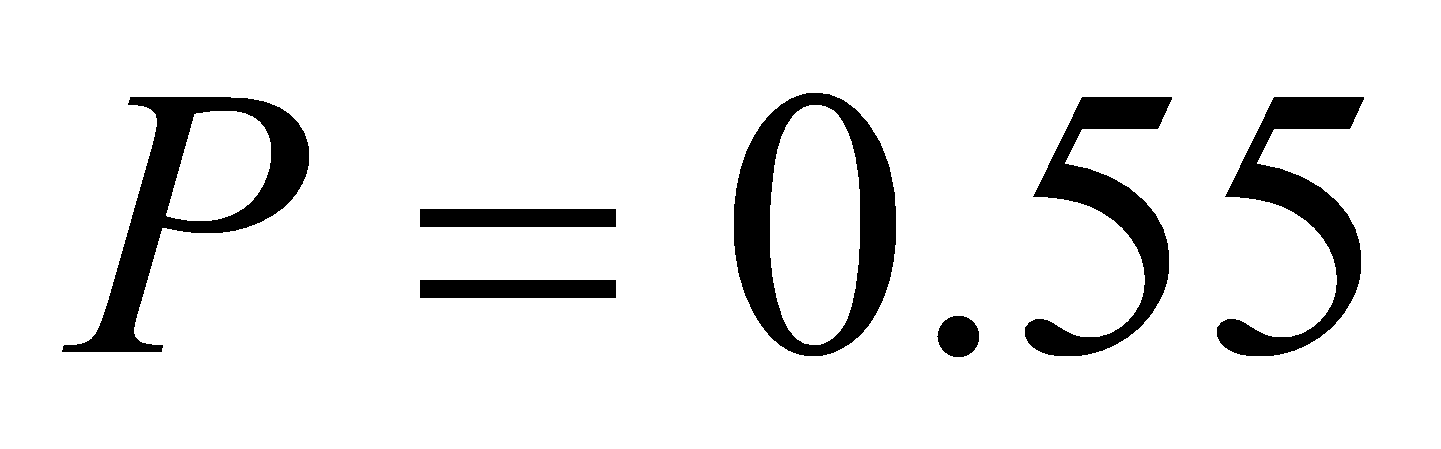 ,
,
 ,
,
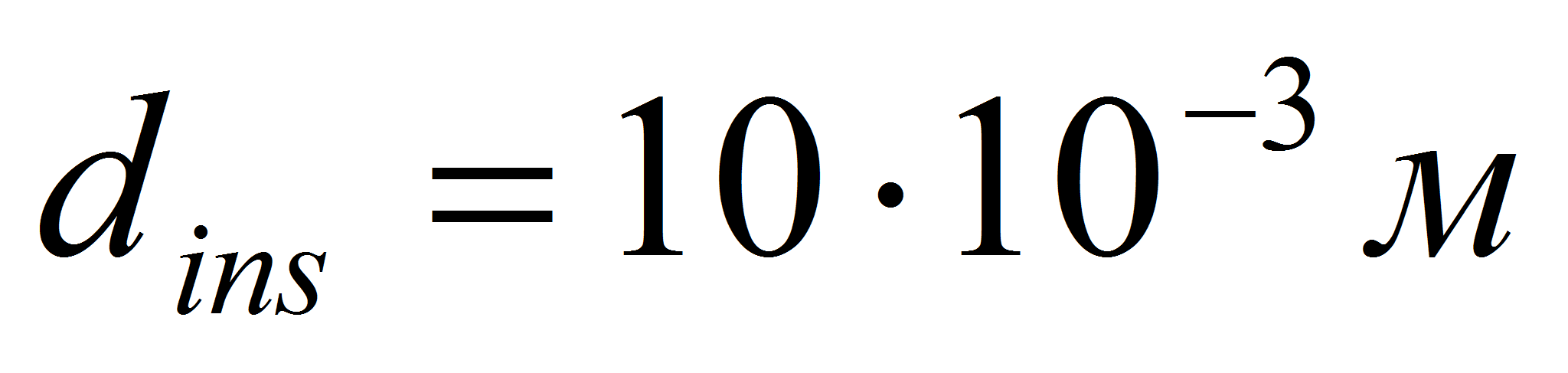 ,
,
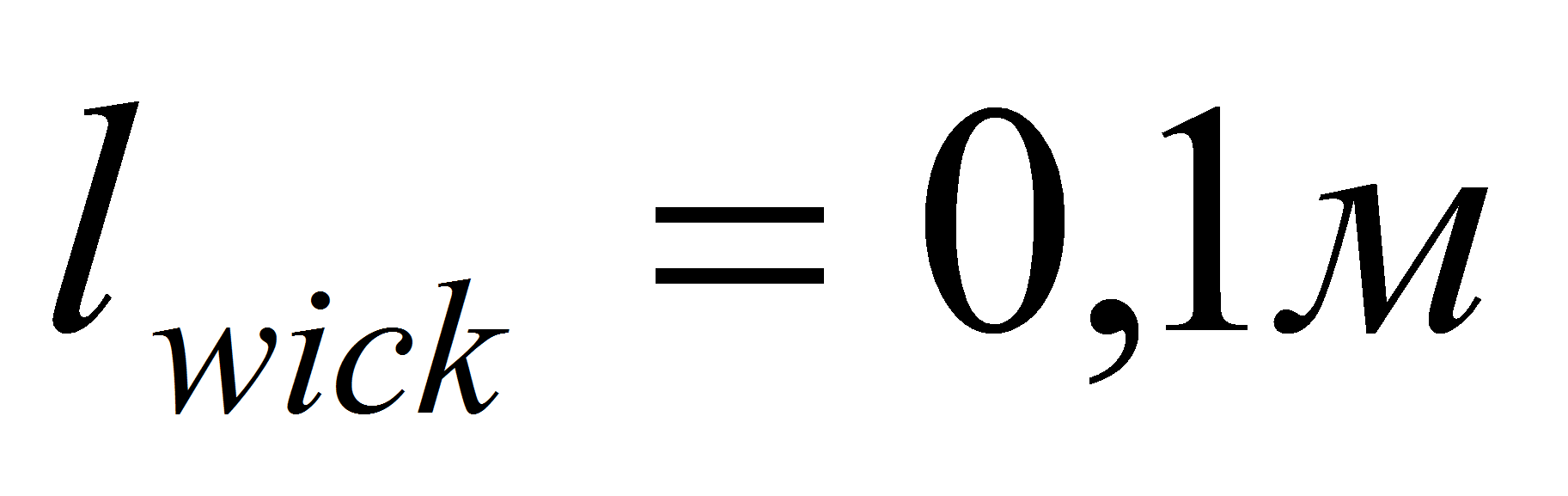 .
.- Параметры паропровода:
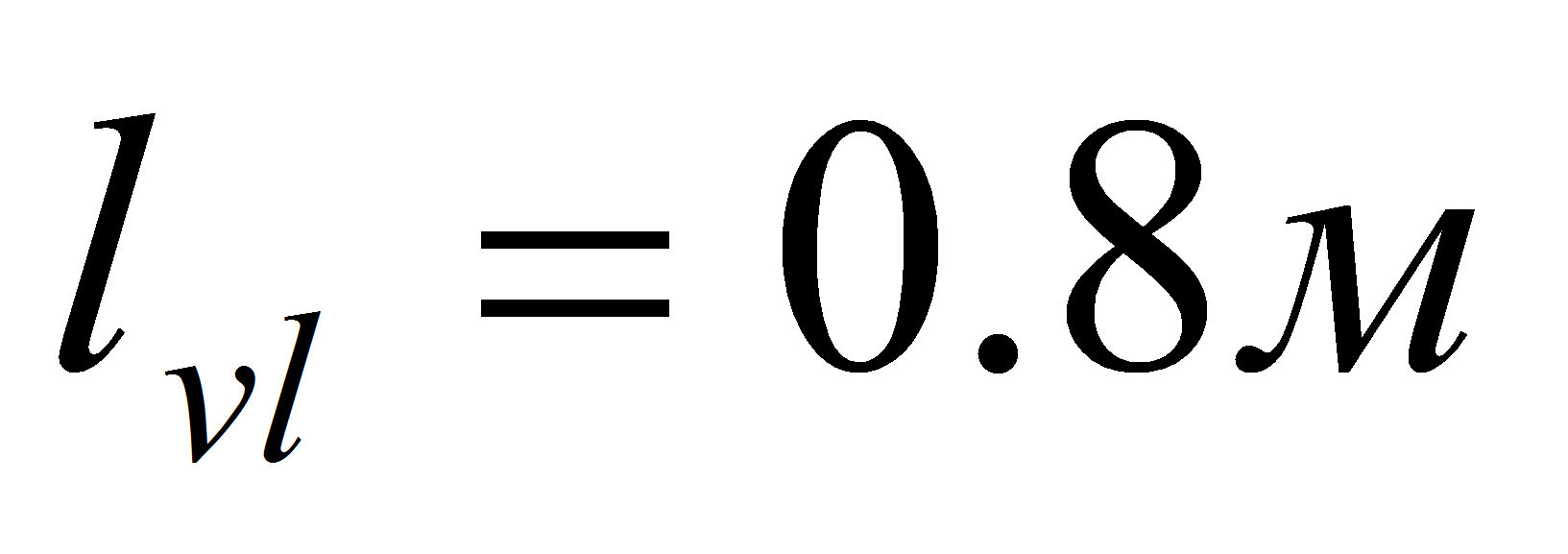 ,
,
 .
.- Параметры конденсатопровода:
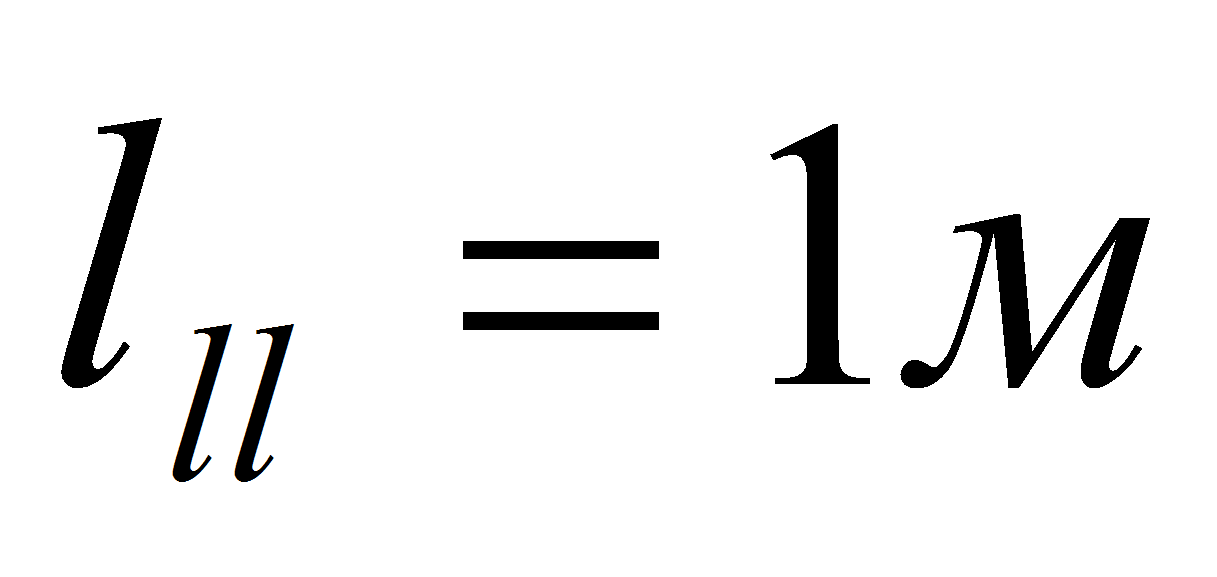 ,
,
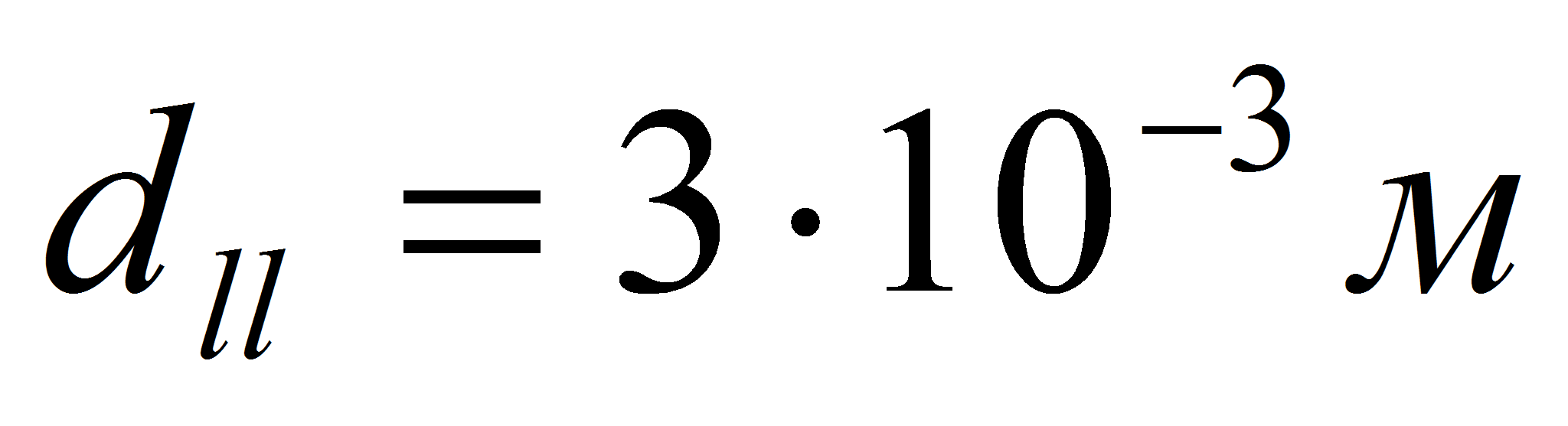 .
.- Параметры пароотводных каналов:
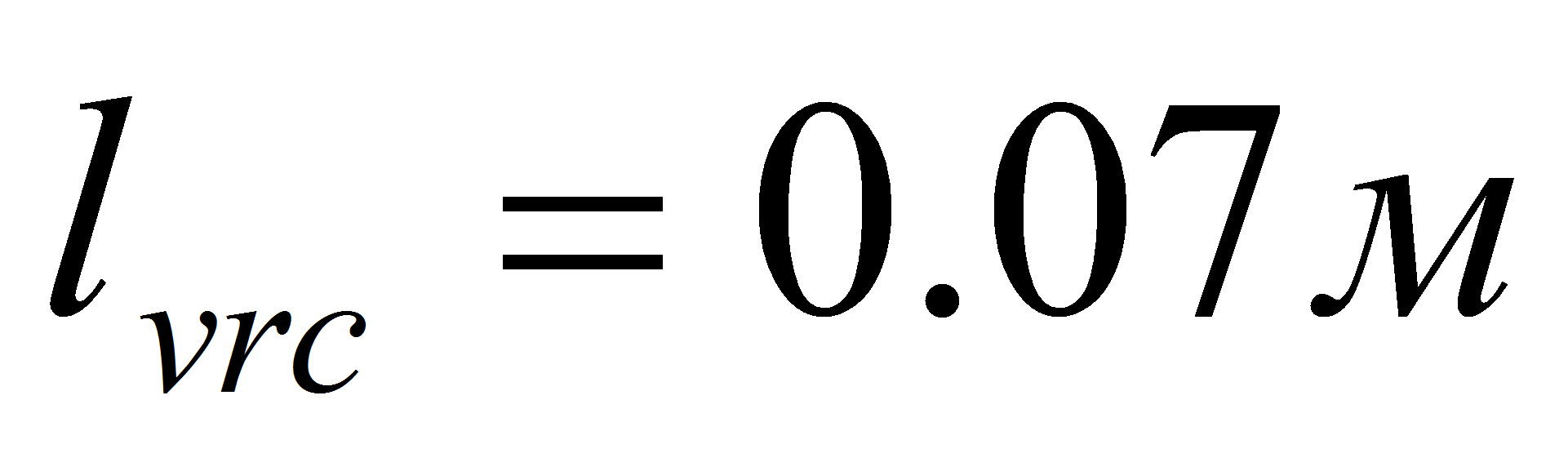 ,
,
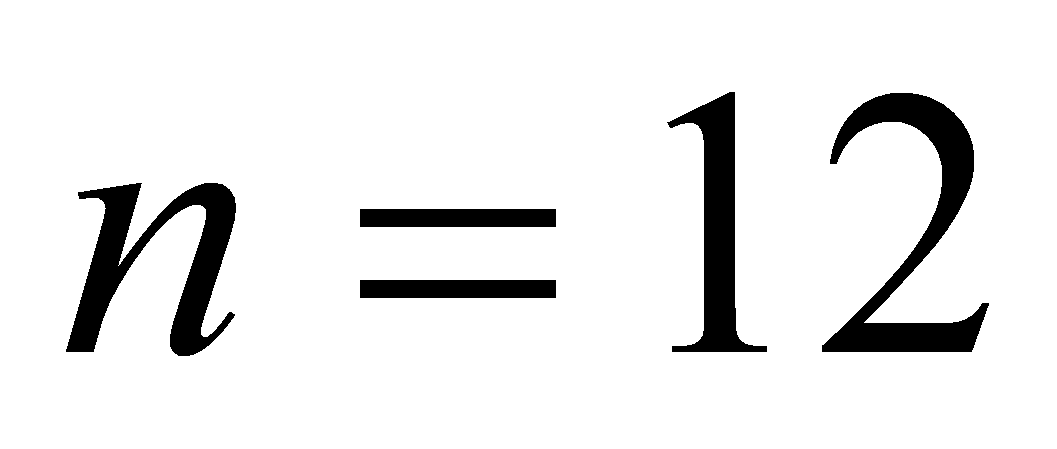 ,
,
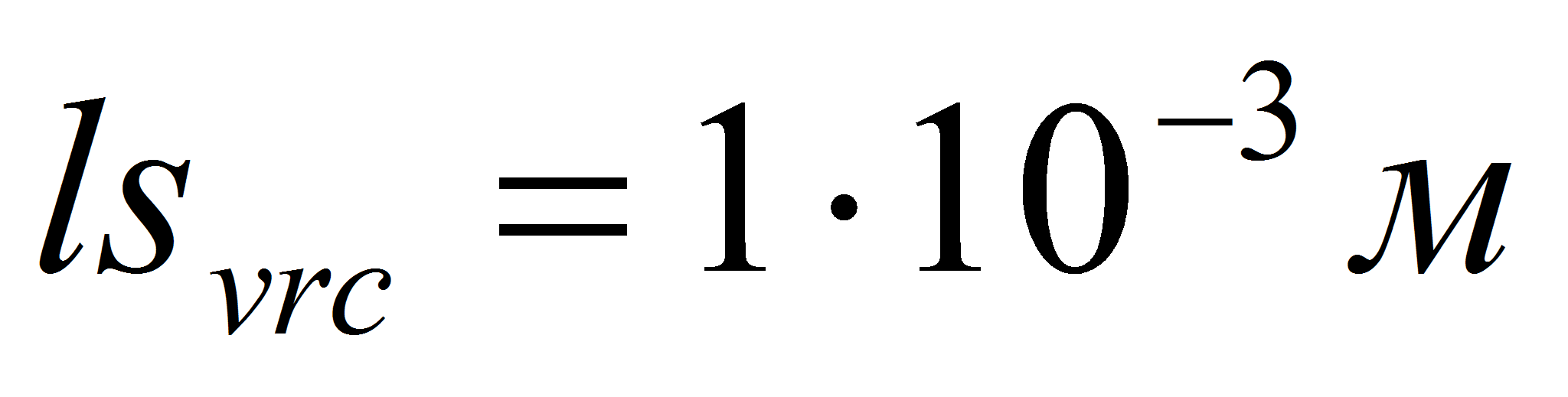 .
.- Параметры конденсатора:
 ,
,
 .
.- Теплоноситель КТТ – аммиак.
- Диапазон рабочих температур КТТ–
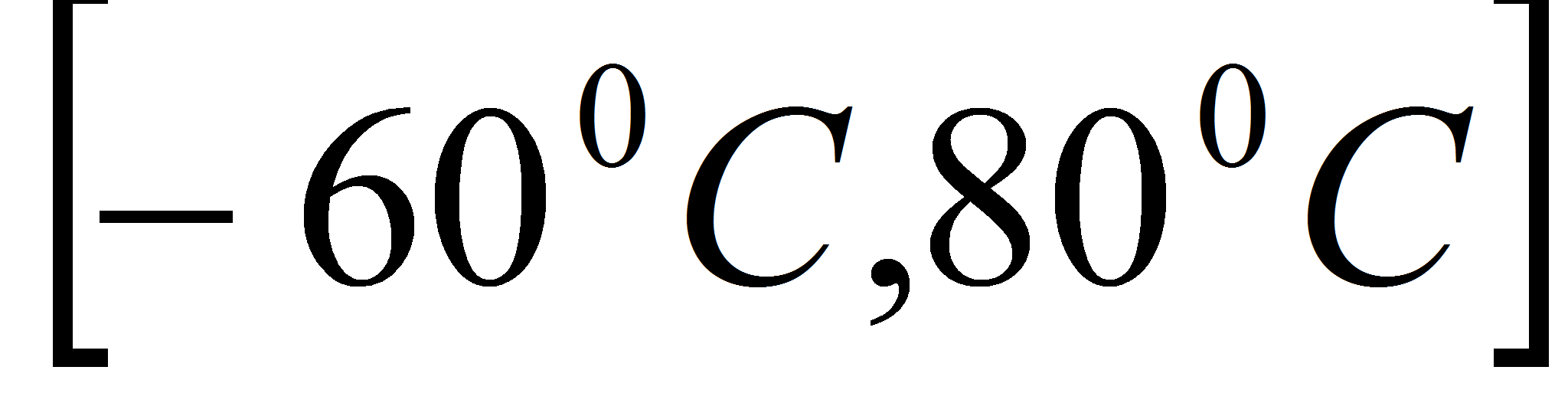
Расчет
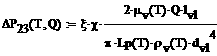
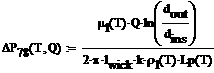
2. Уравнение баланса давлений: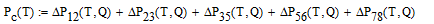
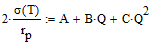
- Поскольку уравнение баланса давлений зависит от тепловой нагрузки и температуры, то, решая данное уравнение относительно
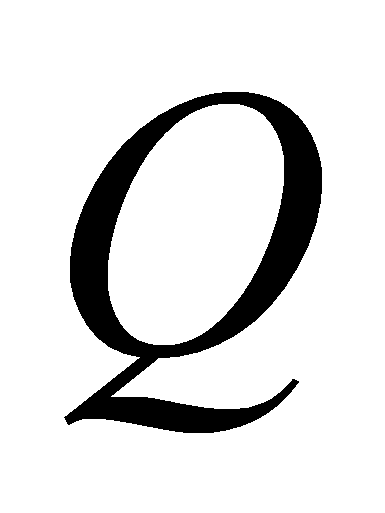 ,
можно получить зависимость максимальной
теплопередающей способности КТТ от температуры пара
,
можно получить зависимость максимальной
теплопередающей способности КТТ от температуры пара
 .
.- 3. График зависимости максимальной теплопередающей способности КТТ от температуры пара (рис. 2):
Рис. 2. Зависимость теплопередающей способности КТТ от температуры пара
-
4.
Результаты расчета и их анализ:
- Определим, где можно наблюдать наибольшие потери давления. В табл. 1 рассмотрен случай, когда температура пробегает три значения:
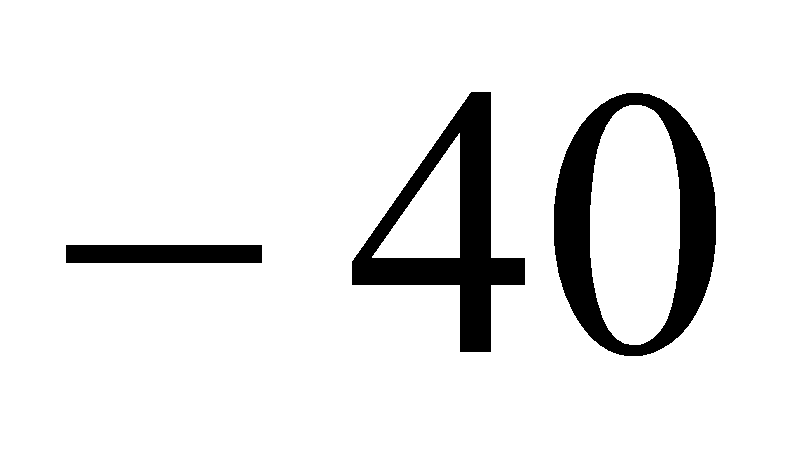 ,
,
 и
и
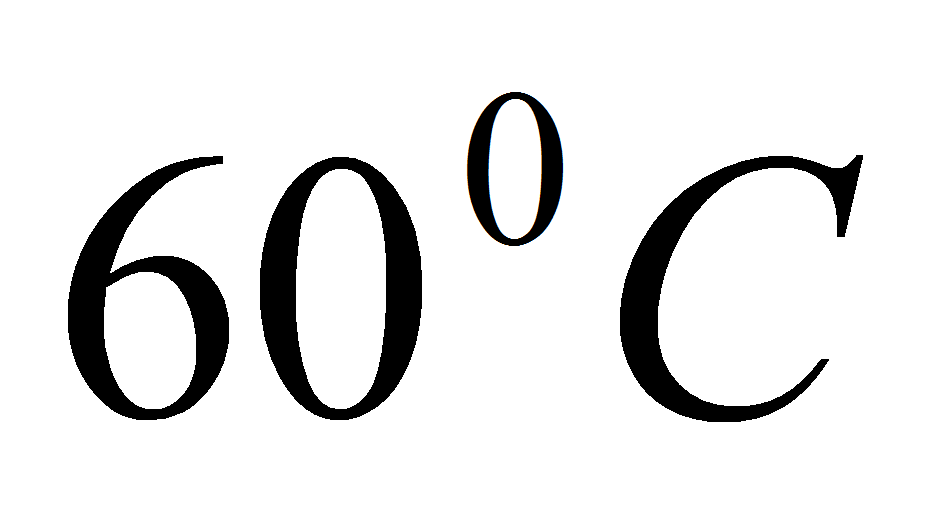 .
.
- Определим, где можно наблюдать наибольшие потери давления. В табл. 1 рассмотрен случай, когда температура пробегает три значения:
Таблица 1. Потери давления на различных участках КТТ
- Так
как потери давления в тепловой трубе компенсируются капиллярным
давлением, то именно оно и принимает наибольшие значения. Также
большие значения принимают величины потерь давления в капиллярной
структуре, паропроводе и пароотводных каналах. Потери давления в
конденсатопроводе обычно пренебрежимо малы по сравнению с
максимальным капиллярным давлением, поэтому их часто не учитывают.
- Теплопередающая способность данной контурной тепловой трубы принимает наибольшие значения в диапазоне температур от 30 0С до 50 0С.
- Влияние геометрических параметров теплотранспортных участков на максимальную теплопередающую способность КТТ. Существенное влияние на величину теплопередающей способности оказывают геометрические параметры теплотранспортных участков КТТ – конденсатопровода и паропровода, в особенности такая величина, как диаметр. Проследим данное влияние на графиках, считая диаметр паропровода равным диаметру конденсатопровода (рис. 3).
- Теплопередающая способность данной контурной тепловой трубы принимает наибольшие значения в диапазоне температур от 30 0С до 50 0С.
Рис.
3. Вид зависимости
![]() при
разных диаметрах теплотранспортных участков:
при
разных диаметрах теплотранспортных участков:
1 –
для
![]() ,
2 – для
,
2 – для
![]() ,
3 – для
,
3 – для
![]() ,
4 – для
,
4 – для
![]()
-
Как
видно из представленных графиков, максимальная теплопередающая
способность увеличивается с увеличением диаметра транспортных
участков КТТ. Это явление можно объяснить тем, что с увеличением
диаметра теплотранспортных участков уменьшается величина потерь
давления. Данный факт и приводит к росту теплопередающей
способности. Это свойство можно использовать в процессе расчета
контурной трубы, когда необходимо учитывать величину теплового
потока, подводимого к испарителю. Чем больше будет диаметр
теплотранспортных участков, тем при больших мощностях сможет
работать контурная тепловая труба.
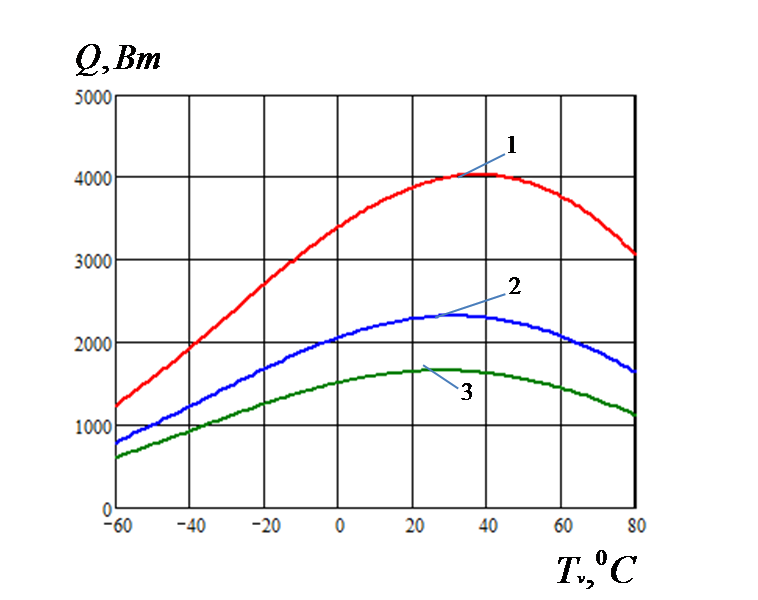
- Влияние величины радиуса пор капиллярной структуры на максимальную теплопередающую способность КТТ. Характеристики капиллярной структуры во многом обеспечивают работу тепловой трубы. Самым главным параметром, который необходимо учитывать, является радиус пор капиллярной структуры. Именно от него зависит величина капиллярного давления, обеспечивающего эффективную работу контурной тепловой трубы. В данной задаче рассчитывалась тепловая труба, в которой фитиль изготовлен из спеченного никелевого порошка. Из справочных данных известно, что размер пор у таких структур колеблется от одного микрона до трех. Рассмотрим зависимости
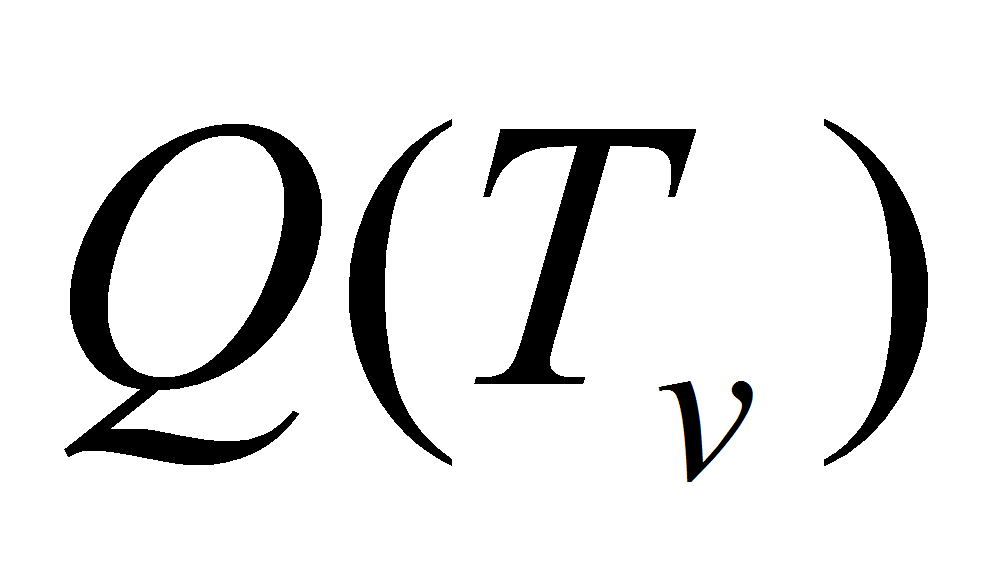 при разных значениях радиусов пор (рис. 4).
при разных значениях радиусов пор (рис. 4).
Рис.
4. Вид зависимости
![]() при разных размерах пор капиллярной структуры:
при разных размерах пор капиллярной структуры:
-
Из
графиков видно, что контурная тепловая труба с меньшим размером пор
капиллярной структуры может работать при больших мощностях теплового
потока, чем контурная труба с большим размером пор КС. Этот вывод
можно подтвердить теоретически, анализируя формулу для капиллярного
давления, которая предоставляет обратно пропорциональную зависимость
величины перепада капиллярного давления от радиуса капиллярной
структуры.
- Влияние ориентации КТТ на потери давления на различных участках трубы. Существует большое количество вариантов использования контурных тепловых труб, среди которых можно найти конструкторские решения, предполагающие различные ориентации трубы в пространстве. Разная ориентация КТТ влияет на потери давления, связанные с гидростатическим сопротивлением. Самые большие потери наблюдаются при вертикальном расположении КТТ, когда угол наклона тепловой трубы к горизонту
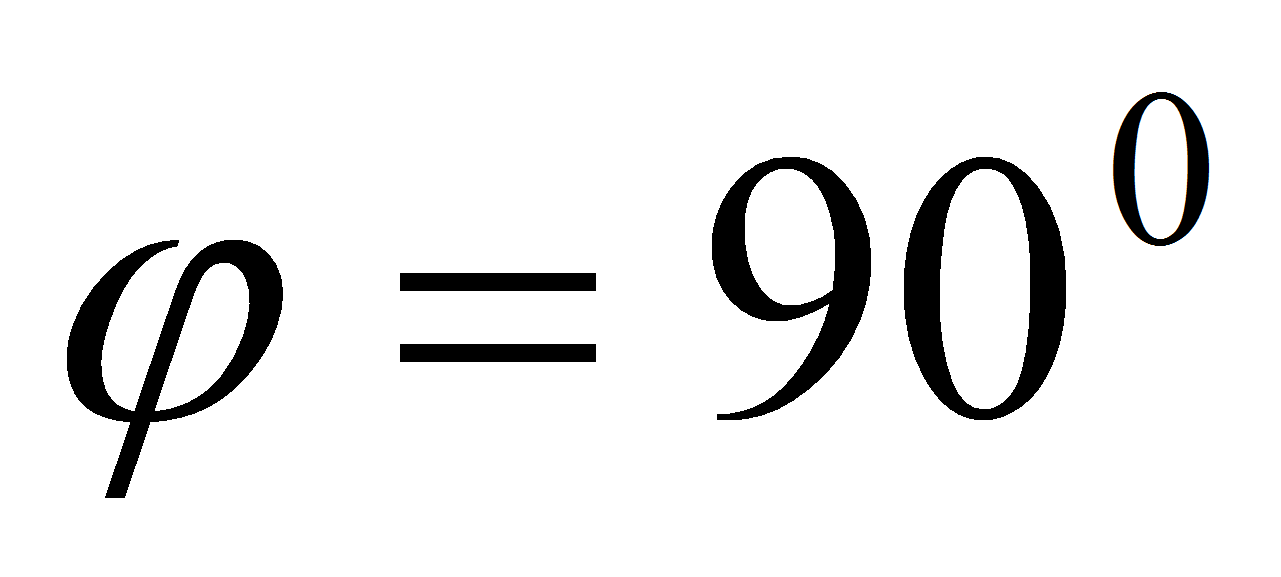 .
.- При угле наклона
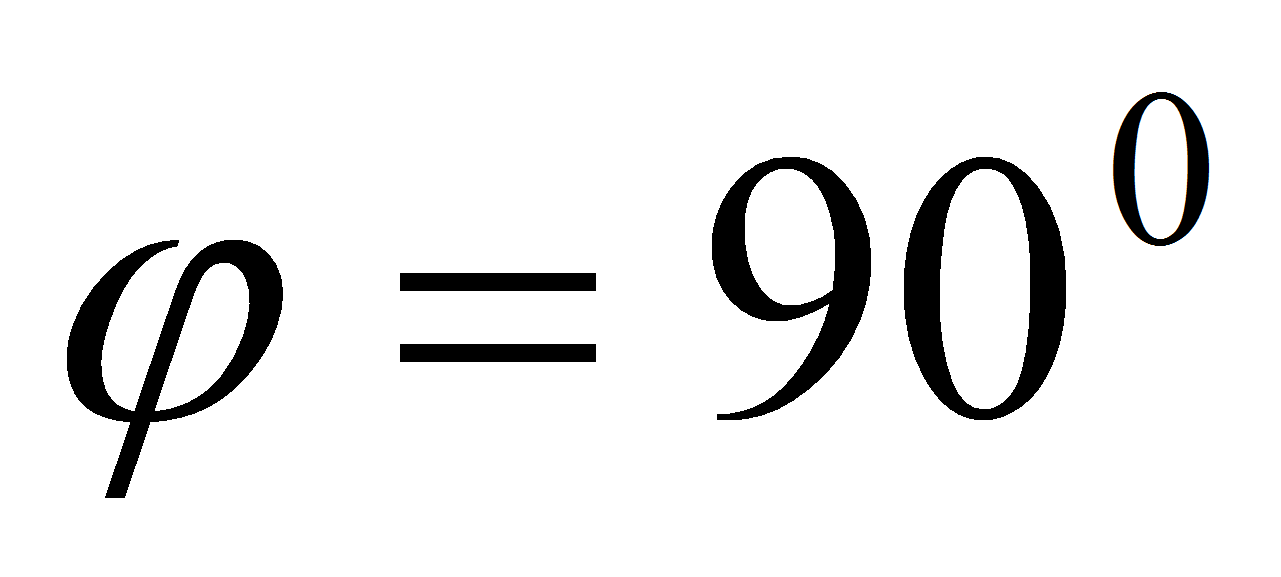 наблюдается резкое возрастание величины потери в конденсатопроводе,
связанное с увеличением гидростатического сопротивления. Однако
такая ориентация контурной тепловой трубы в пространстве оказывает
небольшое влияние на величину теплопередающей способности, хотя в
случае
наблюдается резкое возрастание величины потери в конденсатопроводе,
связанное с увеличением гидростатического сопротивления. Однако
такая ориентация контурной тепловой трубы в пространстве оказывает
небольшое влияние на величину теплопередающей способности, хотя в
случае
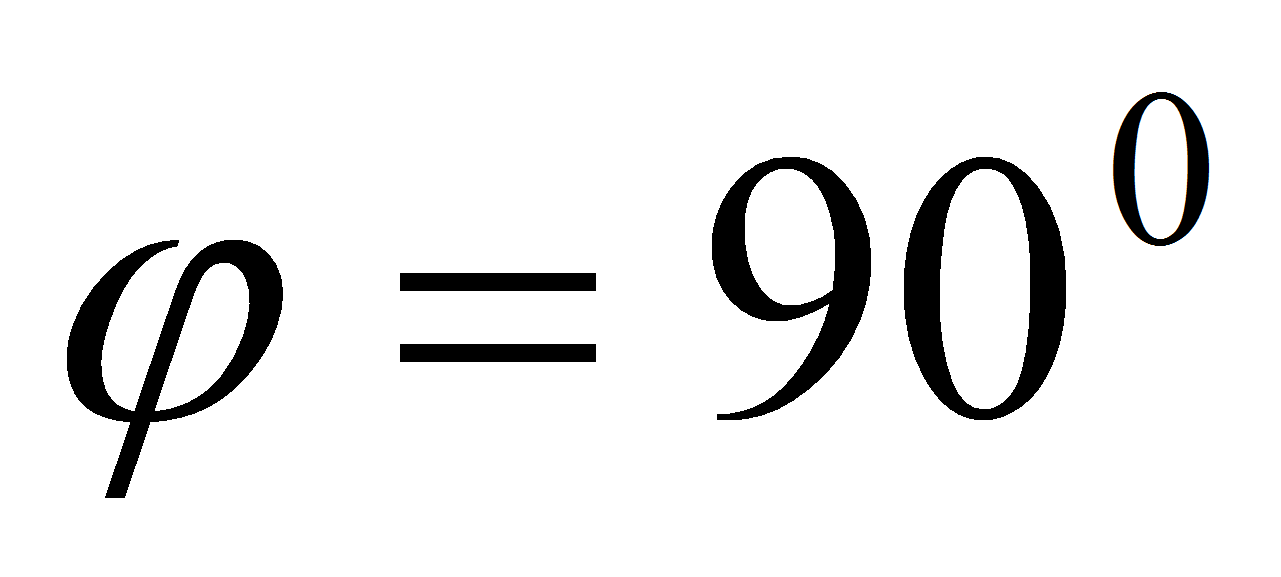 наблюдается ее небольшое снижение. Прежде всего, это связано с тем,
что наибольший вклад в уравнение баланса давлений вносит капиллярное
давление. Именно использование капиллярных сил в КТТ обеспечивает
этим установкам более высокую работоспособность и более широкие
сферы применения по сравнению с обычными тепловыми трубами.
наблюдается ее небольшое снижение. Прежде всего, это связано с тем,
что наибольший вклад в уравнение баланса давлений вносит капиллярное
давление. Именно использование капиллярных сил в КТТ обеспечивает
этим установкам более высокую работоспособность и более широкие
сферы применения по сравнению с обычными тепловыми трубами.
- Все остальные потери давления от ориентации в пространстве не зависят, следовательно, являются постоянными величинами для любой конфигурации КТТ.
Рис. 5. Зависимость теплопередающей способности от ориентации тепловой трубы в пространстве:
1 –
вид зависимости в случае горизонтальной ориентации КТТ (![]() ),
2 – вид зависимости в случае вертикальной ориентации КТТ (
),
2 – вид зависимости в случае вертикальной ориентации КТТ (![]() )
)
-
Из
рис. 5 видно, что в случае, когда КТТ ориентирована вертикально,
поле массовых сил оказывает влияние на теплопередающую способность
контурной тепловой трубы, но, в данном случае, несущественное. Таким
образом, можно сделать вывод: контурные тепловые трубы способны
эффективно работать при любой ориентации их в пространстве.
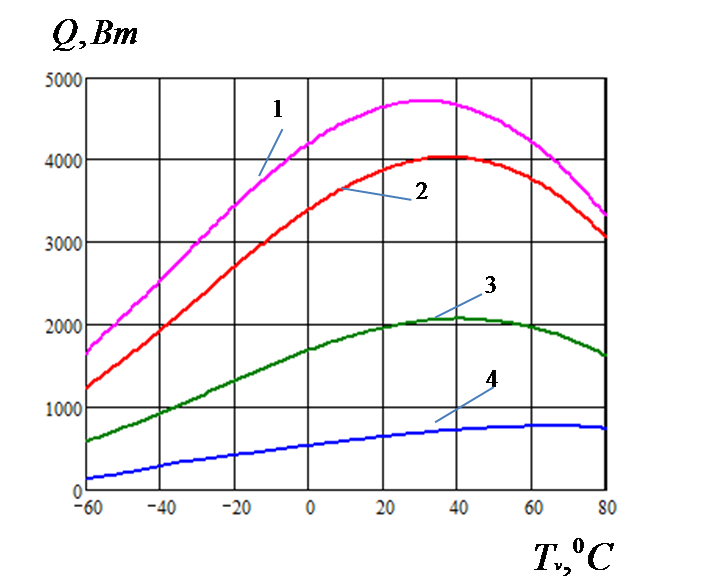
- Влияние режима течения пара на максимальную теплопередающую способность КТТ. Режим течения пара является фактором, способным повлиять на теплопередающую способность контурной тепловой трубы. Он влияет на величину потерь давления в паропроводе и в паровой фазе конденсатора, поскольку эти величины существенно зависят от режима течения пара – при переходе от ламинарного режима к турбулентному они возрастают. Увеличение величин потерь давления приводит к снижению теплопередающей способности, так как она обратно пропорциональна им. Рассмотрим зависимости теплопередающей способности от температуры с учетом режима течения пара (рис. 6).
Рис. 6. Зависимость максимальной теплопередающей способности от режима течения пара:
1
– в случае ламинарного
режима течения (![]() ),
2 – в случае переходного режима (
),
2 – в случае переходного режима (![]() ),
3– в случае развитого турбулентного режима (
),
3– в случае развитого турбулентного режима (![]() )
)
-
Из
графиков видно, что при переходе от ламинарного к турбулентному
режиму течению пара происходит «снижение» максимума
зависимости
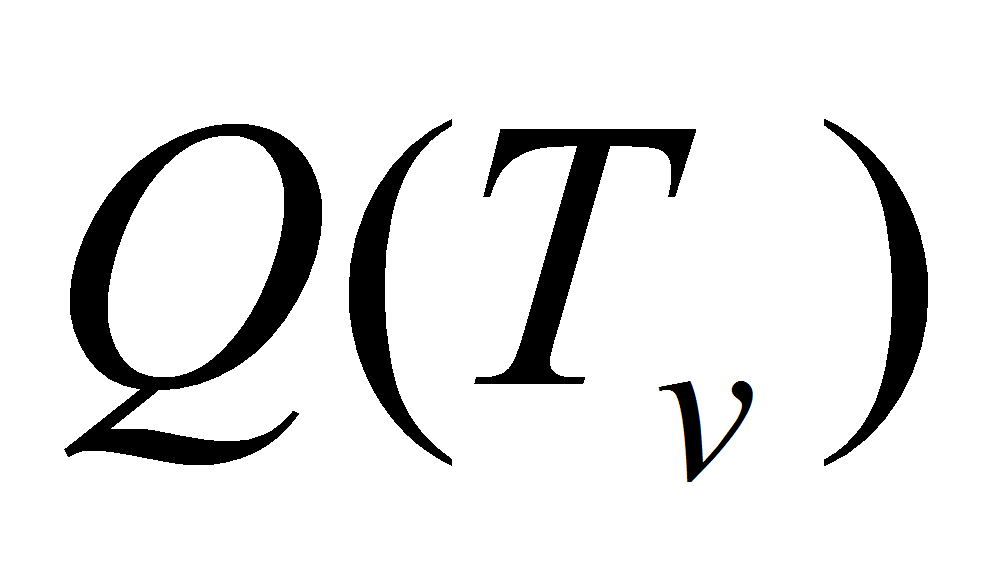 .
.
- Таким образом, можно сделать вывод, что при турбулентном режиме течения пара контурная тепловая труба способна принимать тепловые потоки меньших величин, нежели при работе в ламинарном режиме. Расчеты показывают, что для выбранной нами конфигурации тепловой трубы и размеров паропровода и конденсатопровода, имеет место развитый турбулентный режим во всем температурном диапазоне.
- Заключение. Контурные тепловые трубы являются альтернативными системами терморегулирования, работающими без дополнительных источников энергии [4, с.150]. Они представляют собой теплопередающие устройства, которые способны передавать большие тепловые потоки на значительное расстояние. КТТ обладают основными достоинствами обычных тепловых труб, однако лучше адаптируются к различным условиям эксплуатации и допускают широкую возможность для различных конструктивных воплощений.
- Основные результаты работы можно сформулировать следующим образом:
- 1) исследована теория тепловых труб, а также основные математические зависимости;
- 2) изучены основные физические процессы, протекающие в тепловых трубах;
- 3) произведен расчет максимальной теплопередающей способности аммиачной контурной трубы;
- 4) составлена программа, позволяющая рассчитывать характеристики КТТ в пакете MathCAD;
- 5) произведен анализ влияния на величину теплопередающей способности различных характеристик контурной тепловой трубы, таких как радиус пор капиллярной структуры, геометрические параметры теплотранспортных участков, ориентация КТТ в пространстве;
- 6) сделаны выводы о воздействии режима течения пара на максимальную теплопередающую способность КТТ.
- Практическая ценность данной работы заключается в том, что была разработана компьютерная программа, которая позволяет проводить инженерные расчеты по выбору оптимальных характеристик контурной тепловой трубы, а именно по определению максимальной теплопередающей способности контурной тепловой трубы.
- В ходе работы поставленные задачи были решены, обозначенная цель достигнута.
- Литература:
- Таким образом, можно сделать вывод, что при турбулентном режиме течения пара контурная тепловая труба способна принимать тепловые потоки меньших величин, нежели при работе в ламинарном режиме. Расчеты показывают, что для выбранной нами конфигурации тепловой трубы и размеров паропровода и конденсатопровода, имеет место развитый турбулентный режим во всем температурном диапазоне.
- Контурные тепловые трубы - высокоэффективные теплопередающие устройства. - http: // www.uni.itbu.ru
- Майданик Ю. Ф., Ферштатер Ю. Г., Пастухов В. Г. Контурные тепловые трубы: разработка, исследование, элементы инженерного расчета. Свердловск, 1989. (Препр. / УрО АН СССР. Ин-т теплофизики; № 86). С. 52.
- Ферштатер Ю. Г. Теплообмен в тепловых трубах с разделенными каналами: Дис. к-та физ-мат. наук. Свердловск, 1988. С. 194.
- Кисеев В. М. Физика теплопередающих систем / В. М Кисеев. Екатеринбург: изд-во Урал, ун-та, 2006. С. 188.
- Чи С. Тепловые трубы: Теория и практика /С. Чи. Пер. с англ. В. Я. Сидорова. М.: Машиностроение, 1981. С. 207.
- Майданик Ю. Ф. Достижения и перспективы развития контурных тепловых труб // 4-я конференция по тепломассообмену, Москва, 2006.
- Дан П. Д. Тепловые трубы. / П.Д. Дан, Д. А. Рей. Пер. с англ. М.: Энергия, 1979. С. 272.
- Елисеев В. Б. Что такое тепловая труба? / В. Б. Елисеев, Д. И. Сергеев. М.: Энергия, 1971. С. 136.
- Исаченко В. П. Теплопередача. Учебник для вузов / В. П. Исаченко, В. А. Осипова, А. С. Сукомел. Изд. 3-е, перераб. и доп. М.: Энергия, 1975. С. 488.
- Исследование основных факторов, определяющих теплотранспортные характеристики контурной тепловой трубы. - http: // www.referun.com
- Ферштатер Ю. Г. Аналитическое исследование и основы инженерного расчета КТТ // Тепловые трубы: теория и практика: Сб. науч. тр. / Материалы международной школы-семинара, Минск, 1990. Ч. 1. С. 87-94.