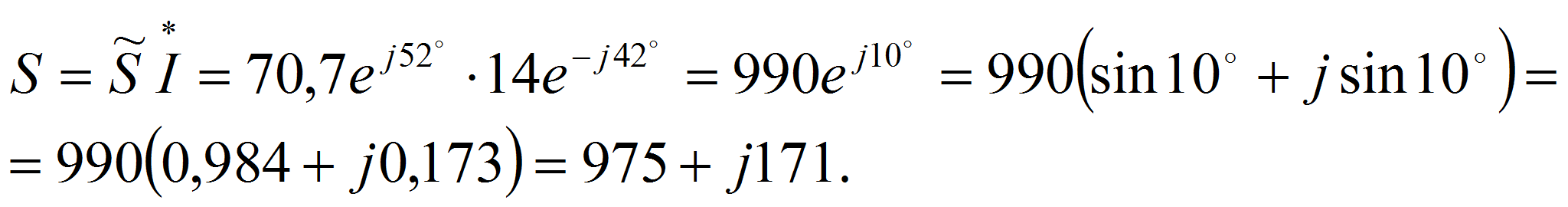Первое упоминание о
«мнимых» числах как о квадратных корнях из отрицательных
чисел относится еще к XVI веку. Итальянский ученый Джироламо Кардано
(1501-1576) в 1545 году опубликовал работу, в которой, пытаясь решить
уравнение
,
он пришел к выражению
.
Через это выражение представлялись действительные корни уравнения:
Таким образом, в работе Кардано мнимые числа появились как
промежуточные члены в вычислениях. Заслуга Кардано состояла в том,
что он допустил существование «несуществующего» числа
,
введя правило умножения:
все остальное стало делом техники.
Однако еще три столетия математики привыкали к этим новым «мнимым» числам, время от времени пытаясь от них избавиться. Только с XIX века, после выхода в свет работ Карла Фридриха Гаусса (1777-1855), посвященных доказательству основной теоремы алгебры, комплексные числа прижились в науке.
Комплексные
числа – один из наиболее подходящих разделов курса
математического анализа для реализации профессиональной
направленности бакалавров по направлению подготовки Информатика
и вычислительная техника. При
изучении комплексных чисел необходимо учитывать применение
математических знаний в общетехнических и специальных дисциплинах, в
частности электротехнике. Применение
комплексных чисел дает возможность использовать законы, формулы и
методы расчетов, применяющиеся в цепях постоянного тока, для расчета
цепей переменного тока, упростить некоторые расчеты, заменив
графическое решение с использованием векторов алгебраическим
решением, рассчитывать сложные цепи, которые другим путем решить
нельзя, упростить расчеты цепей постоянного и переменного токов.
При расчетах цепей приходится проводить математические операции с комплексными числами, поэтому студенты должны уметь выполнять следующие операции: 1) находить модуль и аргумент комплексного числа и комплексное число по модулю и аргументу; 2) переводить комплексное число из одной формы в другую; 3) производить сложение и вычитание, умножение и деление комплексных чисел.
Помимо этого, очень важно научить строить кривую и вектор по уравнению синусоиды, вектор по комплексному числу, определять комплексное число по вектору и уравнению, уравнение по комплексному числу.
В электротехнике тема «Переменный ток» занимает значительное место. Это объясняется тем, что большинство электротехнических установок работает на переменном токе, который изменяется синусоидально.
Уравнение
переменного напряжения имеет вид
,
где u
– мгновенное
значение напряжения;
–
максимальное
значение (амплитуда) напряжения; w
– угловая
частота;
t
–
время;
–
начальный
фазовый угол;
– электрический
угол.
Это уравнение связывает две переменные величины: напряжение u
и время t.
С течением времени напряжение изменяется синусоидально.
Аналогичный
вид имеют уравнения и других синусоидально изменяющихся величин: тока
,
э.д.с.
и т.д.
При расчете цепей переменного тока приходится использовать синусоидально изменяющиеся величины, т.е. производить сложение, вычитание, умножение и деление уравнений указанного выше типа.
Сложение
синусоидальных величин трудоемко, особенно если приходится складывать
большое число уравнений. Синусоидальная величина однозначно
представлена вращающимся вектором, длина которого равна амплитуде, а
начальное положение определяется углом
,
вращение вектора происходит с угловой скоростью w.
Операции производятся с уравнениями, имеющими одинаковую угловую
частоту, то есть все векторы, заменяющие уравнения, вращаются с
одинаковой угловой скоростью. Следовательно, их взаимное расположение
не меняется, отпадает необходимость вращения векторов. Так как
векторы заменяют синусоидальные величины, то сложение или вычитание,
возможно, заменить сложением или вычитанием векторов.
Переменная синусоидальная величина обладает свойствами:
1. Переменная синусоидальная величина может быть однозначно представлена вектором. Длина вектора равна амплитуде; угол наклона равен начальному фазовому углу.
2. Сложение (и вычитание) синусоидальных величин можно заменить сложением (и вычитанием) векторов.
Кроме сложения и вычитания синусоидальные величины приходится умножать и делить. И здесь на помощь приходят комплексные числа.
Комплексное число может быть изображено
на плоскости вектором, длина которого равна модулю комплексного
числа, а угол наклона – аргументу. В электротехнике в отличие
от математики мнимая
единица обозначается буквой j.
Если имеется комплексное число A=a+jb,
то его
можно
представить вектором, где
– модуль комплексного числа;
–
аргумент
комплексного числа.
Комплексное число имеет три формы:
алгебраическую – A=a+jb;
тригонометрическую
–
;
показательную –
.
Комплексное число однозначно представлено вектором, а определенному вектору соответствует определенное комплексное число.
Таким образом, если переменная синусоидальная величина может быть представлена вектором, а определенному вектору соответствует определенное комплексное число, то переменная синусоидальная величина может быть представлена комплексным числом. Такие величины как: напряжение и ток, сопротивление и проводимость, мощность выражаются комплексными числами.
Напряжение
и ток.
Имеется уравнение
.
В электротехнике за длину вектора берется не максимальное, а
действующее значение. Оно обозначается большой буквой U
без индекса и вычисляется путем деления максимального
значения на
.
Синусоидальная
величина, выраженная комплексным числом, называется
комплексом
и обозначается прописной буквой с точкой наверху
.
Комплекс напряжения можно написать в трех формах алгебраической –
,
тригонометрической –
и
показательной –
.
Таким образом, в комплексе напряжения модуль равен действующему значению, аргумент – начальному фазовому углу, активная составляющая – вещественной части комплекса напряжения, реактивная – мнимой части.
Аналогично
для тока:
,
,
,
,
.
Пример.
Дано:
ток в комплексной форме
Написать уравнение тока.
Решение. Для того чтобы написать уравнение, надо знать амплитуду и начальный фазовый угол. Поэтому надо найти модуль – действующее значение и аргумент – начальный фазовый угол заданного комплекса тока:
,
,
,
.
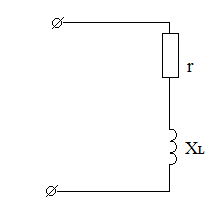
Сопротивление и проводимость. Имеется
цепь (рис. 1): r
– активное сопротивление (лампа накаливания);
– индуктивное сопротивление (катушка); z
– общее сопротивление
цепи, называемое полным.
Рис.1 Рис.2
Сопротивления r,
,
z
образуют прямоугольный треугольник сопротивления
(рис. 2). Угол
– угол сдвига фаз. Сопротивления не являются синусоидальными
величинами, однако отрезок z
может быть выражен комплексным числом, считая, что отрезок r
откладывается по оси вещественных чисел, а отрезок
– по оси мнимых чисел.
Сопротивление в комплексной форме
обозначается буквой Z.
Для цепи на рис.2 комплекс сопротивления записывается:
– алгебраическая форма;
– тригонометрическая форма;
– показательная форма.
Модуль
;
аргумент
.
Таким образом, в комплексе сопротивления модуль равен полному
сопротивлению, а аргумент – сдвигу фаз.
Мощность. Комплекс
мощности получится, если комплекс напряжения умножить на сопряженный
комплекс тока:
,
где
– комплекс мощности,
– сопряженный
комплекс тока.
После умножения получим комплексное число, у которого вещественная часть равна активной мощности, а мнимая часть – реактивной мощности:
,
где P
– активная мощность, Q
– реактивная мощность.
Пример.
,6;
.
Определить активную P
и реактивную Q
мощность.
Решение. Переведем комплексы напряжения и тока в показательную форму, для этого найдем модуль и аргумент тока и напряжения:
,
,
,
,
,
.
Определим сопряженный комплекс тока:
,
Найдем активную и реактивную мощности: P=975Вт, Q=171 вар.
Алгебраическая форма комплексного числа удобна при сложении и вычитании, показательная – при умножении и делении; тригонометрическая служит для перевода показательной формы в алгебраическую.
На занятиях преподаватели могут использовать примеры, не вдаваясь углубленно в электротехнику, задания рассматривая их только с математической точки зрения. В качестве дополнительного материала, самостоятельной работы можно предложить задания типа:
Дано: а)
;
б)
;
в)
;
г)
Найти модуль и аргумент комплексного числа.
Дано: а)
;
б)
;
в)
.
Написать комплексные числа в показательной и алгебраической формах.
Дано: а)
;
б)
;
в)
;г)
;
д)
; е)
; ж)
.
Перевести алгебраическую форму комплексного числа в показательную и наоборот.
Выполнить сложение, умножение, деление комплексных чисел.
Дано: а)
;
б)
;
в)
.
Данная статья поможет преподавателям математики разобраться в вопросе о приложении комплексных чисел в электротехнических расчетах.
Литература:
Теоретические основы электротехники: Теория электрических цепей и электромагнитного поля: учеб. пособие для студ. высш. учеб. заведений / под ред. С.А. Башарина, В.В. Федорова. – М.: Издательский центр «Академия», 2004. – 304 с.
