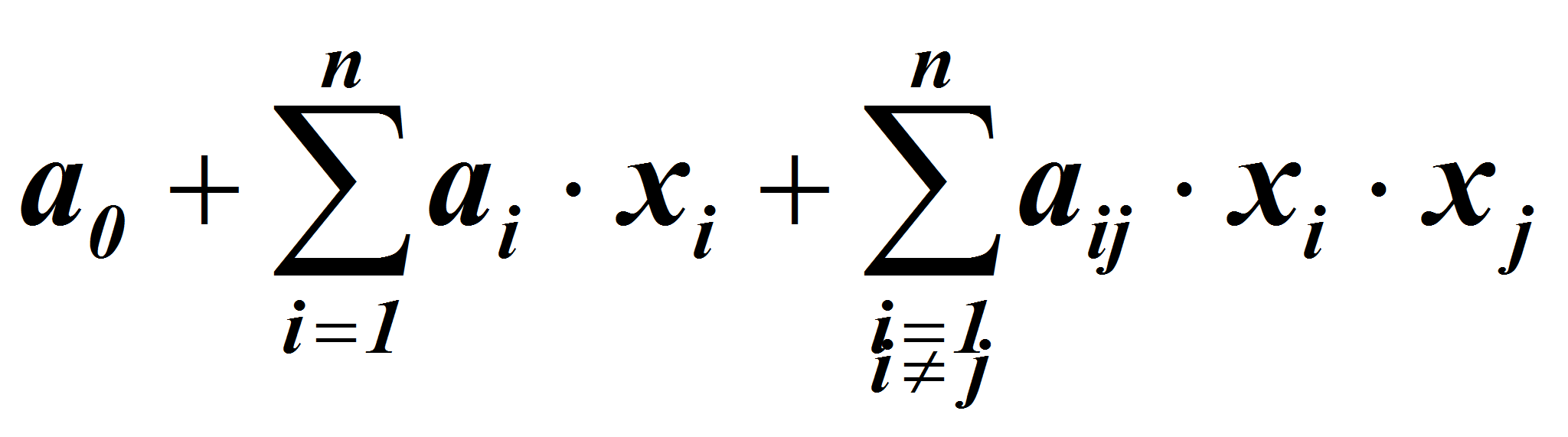Исследование реакции окислительного хлорфосфорилирования синтетического дивинильного каучука под действием PCl3 в присутствии кислорода методом планирования эксперимента

Синтез фосфорсодержащих полимеров в результате химической модификации про-мышленных образцов соединениями фосфора является технологически более удобным и экономически выгодным по сравнению с процессами полимеризации и поликонденсации соответствующих мономеров. Одним из перспективных методов получения полифункциональных полимеров с одновременным введением нескольких функциональных групп в макромолекулу является реакция окислительного хлорфосфорилирования под действием PCl₃, в присутствии кислорода, проводимая на базе дешевых исходных реагентов и легко осуществимая на практике. Несмотря на то, что для низкомолекулярных органических соединений эта реакция глубоко изучена и широко применяется уже давно [1,2], этого нельзя сказать о полимерах. В литературе имеются сведения об окислительном хлор-фосфорилировании лишь некоторых полимеров [3]. Принимая во внимание, что указанные полимеры являются предельными, проведение окислительного хлорфосфорилирования полимеров, содержащих двойную связь (в том числе синтетических дивинильных каучуков (СКД)), и химическое и физико-химическое исследование продуктов превращения последних является весьма актуальным с научной и практической точки зрения.

Поскольку отсутствие математической модели процесса получения фосфохлорированного полимера усложняет его оптимизацию, в данной работе нами была предпринята попытка построить математическую модель данного процесса на основе экспериментально-статистических методов.

Экспериментальная часть

Для установления количественных соотношений, отражающих влияние основных факторов технологического режима, к числу которых относятся: количество PCl₃-Х₁, гр., количество СКД-Х₂, гр., скорость подачи кислорода-Х₃, л&#;ч^-1, продолжительность реакции-Х₄, ч., с выходными параметрами: количество фосфора в полимере-у₁, %, скорость превращения в фосфохлорированный модификат-у₂ г&#;моль&#;(л&#;мин)^-1; был использован метод активного планирования эксперимента [4]. Основной уровень по каждой из независимых переменных и интервалы варьирования выбирали на основе предварительных исследований (табл.1).

Таблица 1

Основной уровень и интервалы варьирования для независимых переменных

Матрица планирования, представляющая планирование факторного эксперимента (ПФЭ) типа 2⁴, записанная в кодовых обозначениях, а также результаты опытов представлены в табл.2.

Таблица 2

Матрица планирования, представляющая ПФЭ типа 2⁴,записанная в кодовых обозначениях, и результаты опытов

Математическое выражение зависимости параметра оптимизации от входных независимых переменных представлено в виде регрессионного уравнения

У_к= (1)

Где У_к-значение параметра оптимизации; x_i,x_j-кодированные обозначения факторов модели, n- число факторов, а₀-величина свободного члена в уравнении регрессии, a_i, a_ij-коэффициенты соответственно линейного эффекта и парного взаимодействия факторов. Кодированные переменные связаны с количеством PCl₃-(Z₁), СКД-(Z₂), скоростью подачи кислорода -(Z₃), продолжительностью реакции -(Z₄) следующими соотношениями:

X₁= ; X₂= ; X₃= ; X₄= ;

На основании результатов ПФЭ были рассчитаны коэффициенты регрессии при помощи следующих выражений:

(2) ;i=1, 2, 3, 4 (3)

; i&#;j; i,j=1, 2, 3, 4 (4)

а₀=4,95&#; а₁=2,48&#; а₂=0,096&#; а₃=-0,1325&#; а₄=2,005

а₁₂=0,0488&#; а₁₃=-0,1175&#; а₁₄=-0,13&#; а₂₃=0,0211&#; а₂₄=0,04&#; а₃₄=-0,044

b₀=0,83·10^-4&#; b₁=0,355·10^-4&#; b₂=-0,0022·10^-4&#; b₃=-0,0063·10^-4&#; b₄=-0,384·10^-4&#;

b₁₂=0,004·10^-4&#; b₁₃=-0,0074·10^-4&#; b₁₄=0,08·10^-4&#; b₂₃=-0,0086·10^-4&#; b₂₄=-0,0051·10^-4&#; b₃₄=0,0014·10^-4.

После вычисления коэффициентов уравнений регрессии проводили статистический анализ, включающий следующие этапы:

1. Оценка дисперсии воспроизводимости (оценка ошибки эксперимента)

2. Проверка значимости коэффициентов уравнения регрессии по критерию Стьюдента;

3. Оценка адекватности модели с использованием критерия Фишера.

Для определения оценки дисперсии воспроизводимости (ошибки эксперимента) S²{у₁} и S²{у₂} поставили дополнительные опыты (m₀=4) в центре планирования и рассчитали значения S² по формуле (5), где -cреднее значение выходного параметра в центре плана; -опытные значение выходного параметра в центре плана; m-1-число степеней свободы для расчета оценки дисперсии. В результате вычислений получены следующие значения: S²{у₁} =0,043; S²{у₂}=0,00258·10^-8 и соответственно среднеквадратичные отклонения S{у₁} =0,207; S{у₂}=0,0508·10^-4

Проверку на значимость полученных коэффициентов проводили по “t” критерию Стьюдента при надежности оценки 0,95 и числе степеней свободы f₁=m₀-1=3.

Используя формулы: t= (6) (7) и подставляя численные значения S{y₁} и S{y₂} в уравнение (7) находим . После этого, используя уравнение (6), находим расчетные значения критерия Стьюдента “t” для каждого коэффициента уравнений у₁ и У₂. Табличное значение t_T=3,18 для числа степеней свободы равного 3.

Расчеты показали, что для уравнения у₁ коэффициенты а₂, а₁₂, а₂₃, а₂₄, а₃₄ незначимы, а для уравнения у₂ незначимыми являются коэффициенты b₂&#; b₃&#; b₁₂&#; b₁₃&#; b₂₃&#; b₂₄&#; b₃₄.. Незначимость этих коэффициентов можно объяснить тем, что данные факторы и выбранные по ним основные уровни близки к оптимуму. С учетом этого, уравнение (1) принимает следующий вид:

у₁=4,95+2,48х₁+2х₄-0,1325х₄-0,1175х₁х₃-0,13 х₁х₄ (8)

у₂=0,83·10^-4+0,355·10^-4х₁-0,384·10^-4х₄+0,08·10^-4 х₁х₄ (9)

Уравнения (8), (9) представляют собой математическую модель, описывающую экспериментальные данные.

3. Оценку адекватности математической модели (8,9) проверяли по критерию Фишера [5], представляющего собой отношение остаточной дисперсии к дисперсии воспроизводимости: 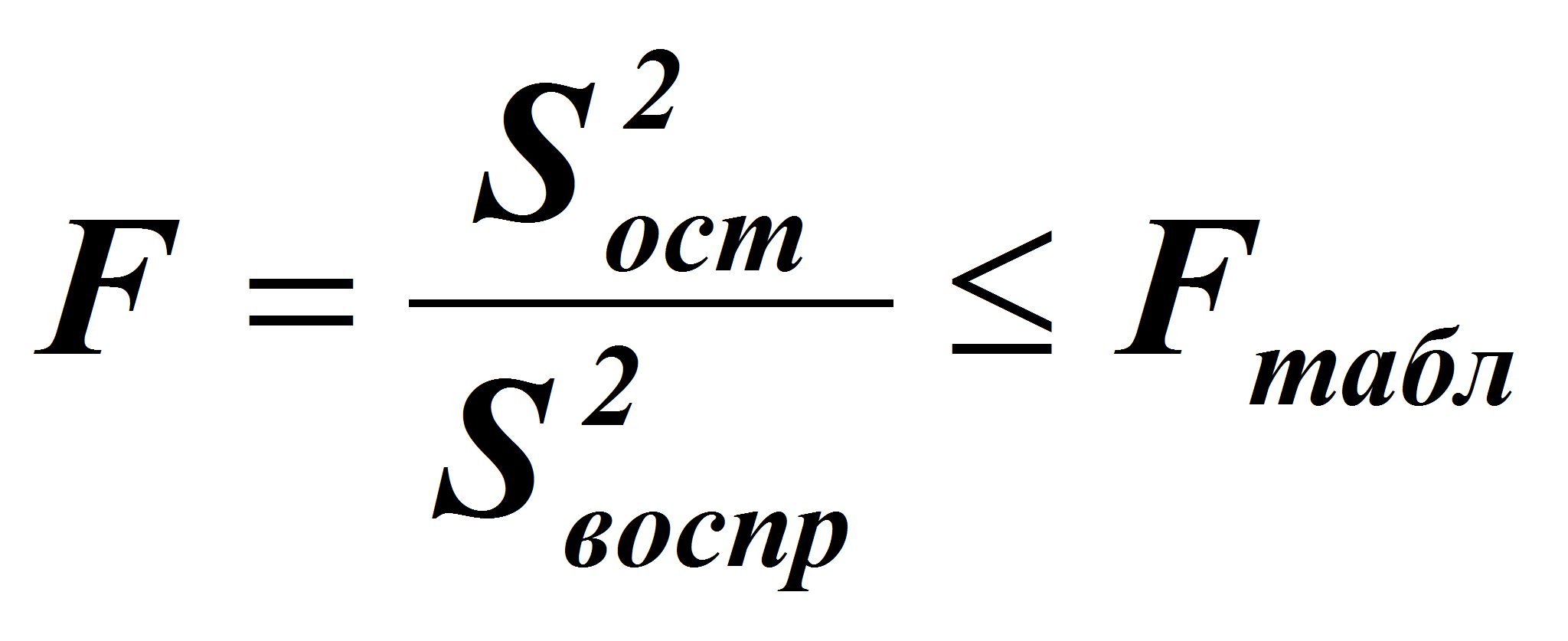&#; (10), где -остаточная дисперсия, определяемая по формуле 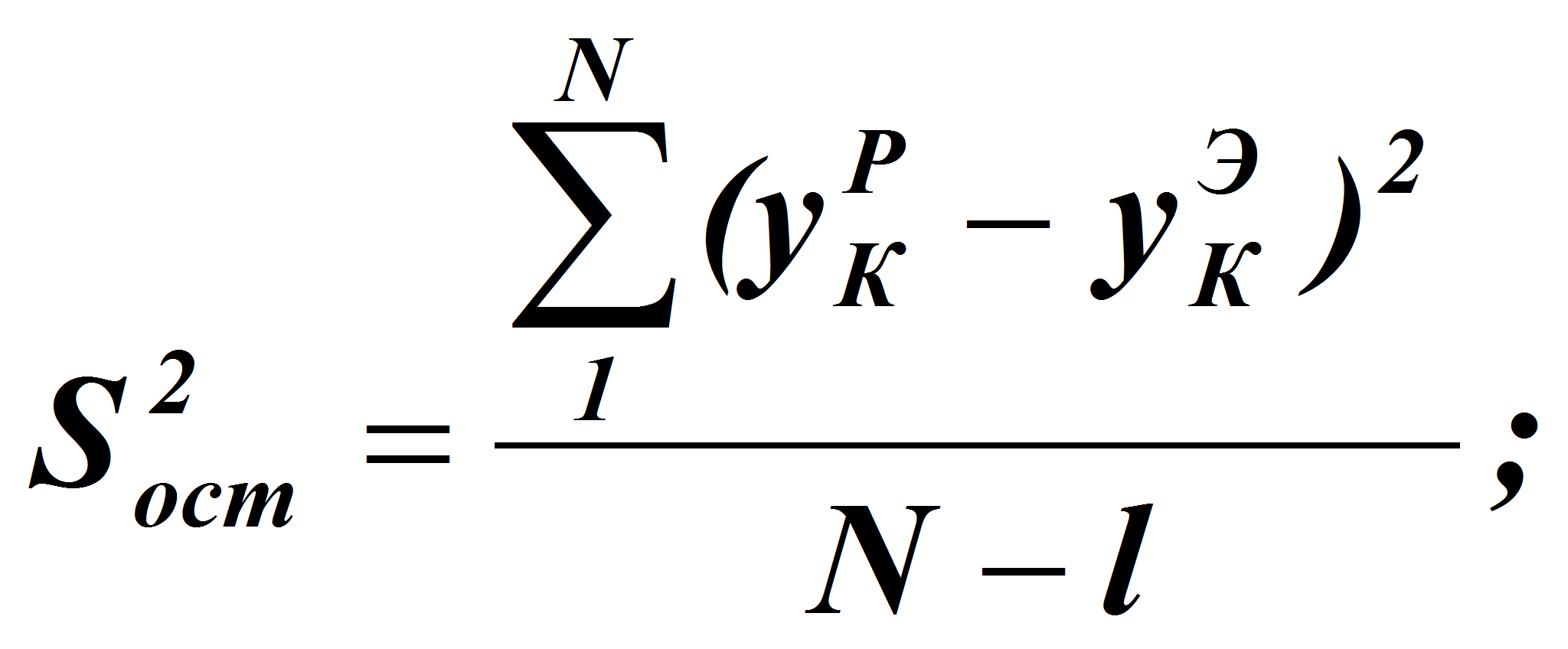(11), где l- число значимых коэффициентов в уравнениях регрессии; -расчетные и экспериментальные значения функции отклика. N-количество опытов в матрице. Подставляя численные значения в уравнения (10) и (11) , получаем:

F₁=1,536 F₂=5,87.

Сравнивая найденные значения F_P критерия с табличными при выбранной доверительной вероятности 95 % и числах степеней свободы f₁=10 и f₂=3, видим, что расчетные значения F_P меньше табличного F_Т =8,84 , что свидетельствует о том, что уравнения регрессии (8,9) адекватно описывает поверхность отклика. Следовательно они могут служить статистической моделью закономерностей изменения параметров процесса.

Далее возникает задача нахождения таких значений входных переменных, которые позволяют найти максимум содержания фосфора в полимере и скорость превращения СКД. По величинам и знакам линейных коэффициентов уравнений поверхностей откликов можно судить о степени влияния отдельных факторов на величину критерия оптимизации. Чем больше величина а_i для соответствующего фактора, тем сильнее его влияние.

На основании уравнений(8,9) можно предположить, что максимальное значение содержания фосфора в полимере-У₁ можно получить при высоких значениях Х₁ и Х₄ при базовых значениях Х₂ и Х₃. На величину скорости превращения СКД-У₂ влияет высокое значение Х₁ и малая Х₄, при базовых значениях Х₂ и Х₃.

В соответствии с полученными численными значениями коэффициентов уравнения регрессии, а также их знаками, было намечено движение по градиенту. Данные по этому методу приведены в таблице 3. Для решения поставленной задачи уравнение (8,9) из кодированного вида преобразовали в натуральный вид. Получили уравнения в натуральном виде:

У₁=-0,0078+14,25Z₁+0,127Z₂+0,0021Z₃+0,295Z₄-0,0232Z₁Z₃-0,092Z₁Z₄ (12)

У₂=0,954+1,396Z₁-0,007Z₂+0,000224Z₃-0,0646Z₄+0,0342Z₁Z₂-0,00109Z₁Z₃+ 0,0566Z₁Z₄ (13)

Таблица 3

Движение по градиенту полученных численных значений и знаков коэффициентов уравнения регрессии

Так как на введение фосфора в полимер наиболее существенно влияет увеличение количества PCl₃ и продолжительности реакции, по этим параметрам был выбран шаг движения по градиенту. Результаты приведены в табл 3.

Поскольку на скорость превращения СКД наиболее существенное влияние также оказывает уменьшение количества PCl₃ и продолжительности реакции, то по этим параметрам был выбран шаг движения по градиенту. Результаты приведены в табл 4.

Таблица 4

Результаты расчетов по количеству PCl₃ и продолжительности реакции

Анализируя результаты движения к оптимуму из таблицы 3 видим, что для увеличения выхода У₁ необходимо увеличивать значение Z₁ от среднего к максимуму и далее до 0,6 гр. PCl_3, количество СКД-Z₂ до уровня 0,74, скорость подачи кислорода -Z₃ до уровня 31,25 л&#;час^-1; продолжительность реакции до 19,75 часов. При этих значениях входных переменных на выходе имеем У₁=13,06 % а У₂=1,19&#;10^-4 гּмоль/л&#;мин; Из таблицы 4 следует, что максимум величины У₂, т.е. скорость превращения синтетического дивинильного каучука в фосфохлорированный модификат получается равной 1,78&#;10^-4 при входных значениях Z₁=0,605; Z₂=0,7; Z₃=33,65; Z₄=0,25 часа; при этом величина У₁=8,36 %.

Таким образом, для осуществления процесса с высокой скоростью, с технологической точки зрения, и для введения в полимер большого количества фосфора, необходимо взять значения исходных параметров в соответствии с данными таблицы 3 и 4.

Литература:

1. Flurry R.L., Charles E. Boozer. The Mechanism of the Chlorophosponation of Hydrocarbons by Phosphorus Trichloride and Oxygen.// J.of Org.Chem. -1966. Vol.31, №7-P. 2076-2083.

2. Гуревич И.Е., Догадина А.В., Ионин Б.И., Петров А.А. Окислительное хлорфосфорилирование 4-хлоралкенов //Ж.Об.Х. -1993. -Т.63.- Bып.1.- С.118-126.

3. Хардин А.П., Тужиков О.И., Бондаренко С.Н. Фосфорилирование карбоцепных полимеров // Успехи химии. -1983.-Т.52.- №7.- C.1173-1195.

4. Рузинов Л.П., Слободчикова Р.Н. Планирование эксперимента в химии и химической технологии. М.: Химия, 1980.- 280 с.

5. Matlab-6. The Moth works Inc. All Right Reserved. USA.2000.