Учебной программой 9-классов девятилетних средних общеобразовательных школ Узбекистана по предмету «Черчение», являющемуся продолжением 35-и часового курса с таким же названием, пройденного в 8-м классе, в 19-м и 20-м уроках тоже из 35-и, предусмотрено прохождение темы под названием «Решение творческих графических задач с элементами проектирования». В учебнике и учебных пособиях по данному предмету приведены примеры задач, предлагаемых учащимся по данной теме. В то же время там подчеркивается, что учитель по своему усмотрению может заменить эти задачи, если они удовлетворяют требованиям государственных образовательных стандартов больше, чем предлагаемые.
Подчеркивая огромную заслугу представителей предыдущих поколений учителей черчения (А.Д. Ботвинников, В.А. Буткевич, Е.А. Василенко, В.Н. Виноградов, И.А. Воротников, В.А.Гервер, С.И. Дембинский, В.Ф. Канев, Ю.Ф. Катханова, Л.Н. Коваленко, Е.И. Корзинова, В.И. Кузьменко, М.Н. Макарова, М.Н. Марченко, Е.М. Ольховников, А.А.Павлова, Н.Г. Преображенская, А.С. Пугачев, Н.О. Севастопольский, А. Умронходжаев, Л.М. Эйдельс и др.) по составлению творческих графических задач, все же следует отметить, что считавшийся для учащихся предыдущих поколений весьма привлекательным учебный материал, для учащегося сегодняшнего дня, который растет в окружении развитых информационно-комунникационных технологий, перестает представлять собой особый интерес.
Исходя из такого факта, при поиске сырьевого материала, стóящего преобразовывать в учебный материал для занятий по черчению на тему «Решение творческих графических задач с элементами проектирования», мы обратились к арсеналу изображений, называемых «Невозможные фигуры».
Ниже приводим несколько примеров из «невозможных фигур», взятых из сайтов Интернет.
1. «Куб Эшера» (Рис. 1, а). Название фигуры связано с именем голландского художника Мориса Эшера, жившего в 1898 – 1972 гг.
2. «Трезубец» (Рис. 1, б). Появление этой фигуры в одних местах связывают с именем турецкого физика Хусейна Вилмда, а в других местах художника Нормана Минго (1965 г.).
3. «Треугольник Рейтсварда» (Рис.1, в). Такое название придано этой фигуре, в честь названия журнала, публиковавшего ее впервые в 1934 г.
4. «Треугольник Пенроуза» (Рис. 1, г). Фигура эта опубликована впервые в 1954 г. и названа в честь придумавшего ее известного английского физика и математика Роджера Пенроуза, родившегося в 1931 г.
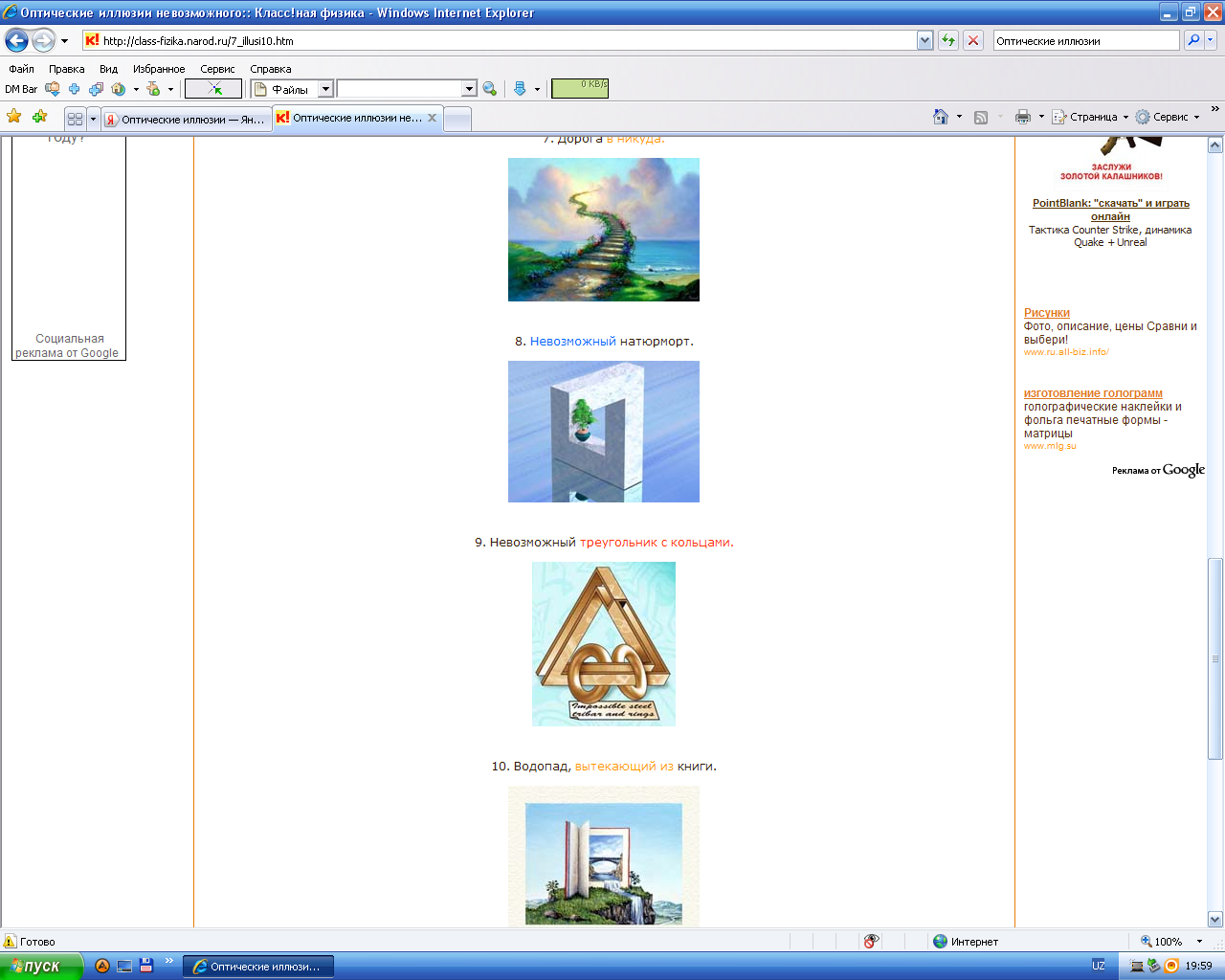
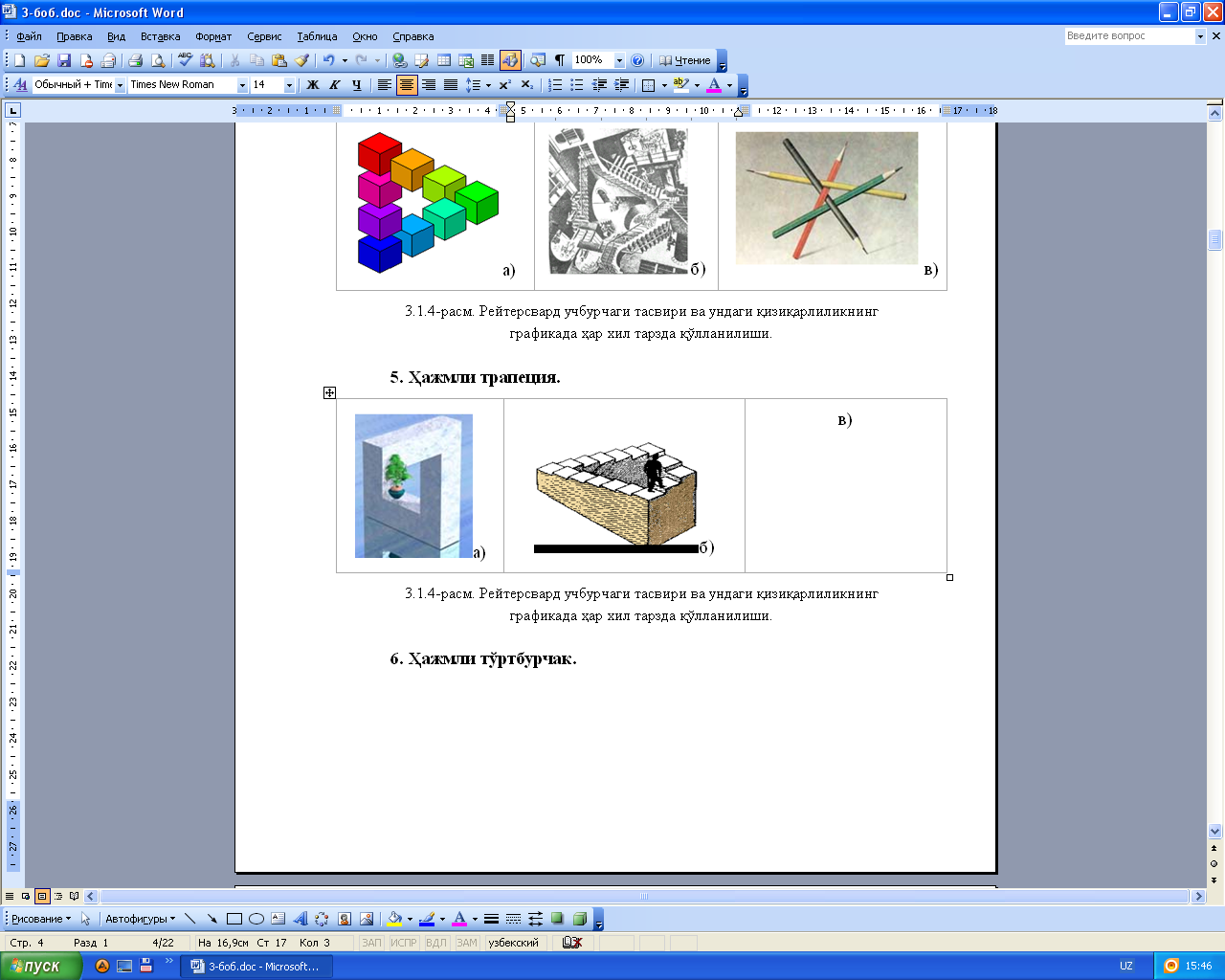
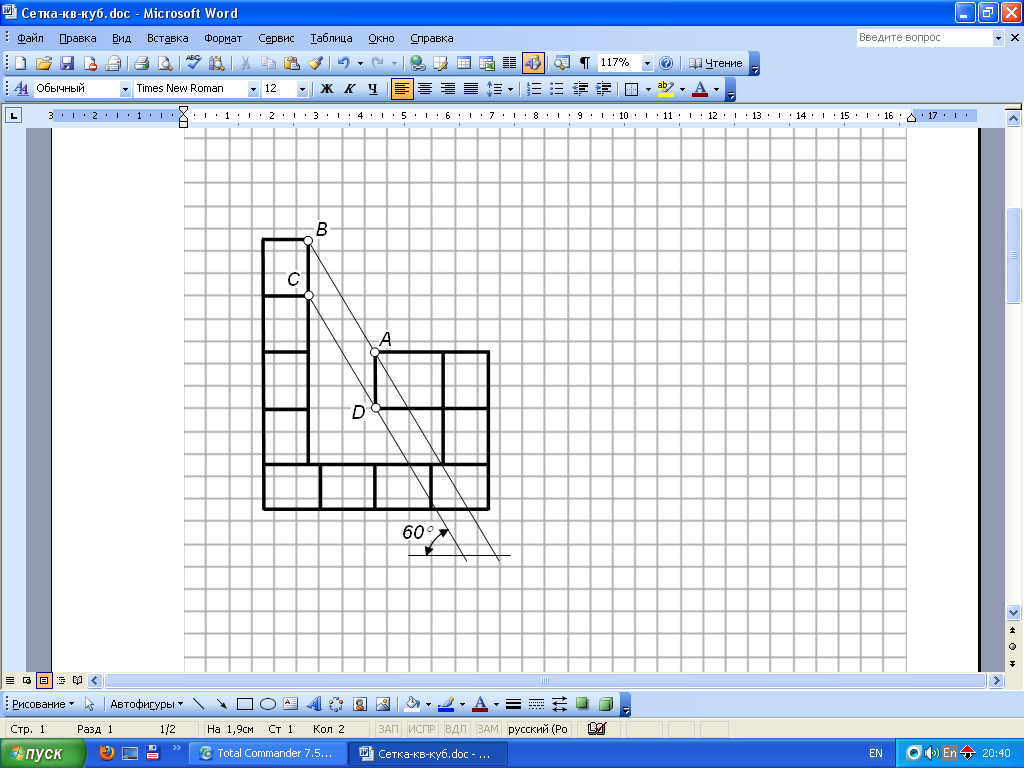
5. «Объемная трапеция» (Рис. 1, д). Автор не выявлен.
6. «Объемный прямоугольник» (Рис. 1, е). Автор не выявлен.
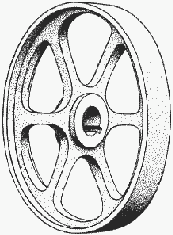
7. Невозможное колесо (Рис. 1, ж). Автор не выявлен.
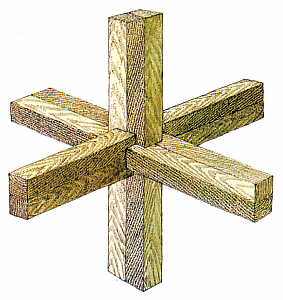
8. Невозможный крест адмирала Макарова (Рис. 1, з). Придумана Митсумасой Анно.
9. «Бесконечная лестница» (Рис. 1, и). Авторство принадлежит Л.С. и Р. Пенроузам (1958 г.) и т.д.
|
|
|
|
||
|
|
|
|
||
|
|
|
|
||
а – «куб Эшера», б – «трезубец», в – «треугольник Рейтерсварда»,
г – «треугольник Пенроуза», д – «объемная трапеция», е – «объемный прямоугольник», ж – невозможное колесо, з – невозможный крест адмирала Макарова, и – бесконечная лестница.
Многие художники умело пользуются свойствами, присущими изображениям невозможных фигур с целью повышения впечатлительности своих произведений. К их числу можно отнести, например, выше упомянутого голландского художника М. Эшера, художников Роджера Шепарда, Сандро дел Прайта и др. В Интернетовских коллекциях «невозможных фигур» можно увидеть весьма заманчивые композиции, выполненные В. Алексеевым, Д.М. Раковым и др.
Чтобы и учителя черчения эффективно использовали свойства, присущие «невозможным фигурам» при составлении графических задач для 2-х часового занятия на тему «Решение творческих графических задач с элементами проектирования», им необходимо будет выполнить некоторую подготовительную педагогическую работу над изображениями этих «фигур».
Для примера возьмем «бесконечную лестницу» (Рис. 1, и).
Изображение этой фигуры там, откуда мы его взяли, представляет собой перспективный рисунок. Однако, учащиеся 9-го класса, за исключением наличия у них представления о таком виде изображений, формировавшихся на уроках рисования, проводившихся в предыдущих классах, не обладают достаточными знаниями, навыками и умениями, необходимыми для геометрического построения перспективных изображений. Значит, данную разновидность изображений надо будет преобразовывать в разновидность изображений, знакомую учащимся. Такой разновидностью изображений для учащихся 9-х классов, является стандартная изометрия. Данные виды изображений как с помощью чертежных инструментов, так и «от руки», легко создать на специально разграфированных листах, приводимых на рис. 2. Эти листы нетрудно изготовить и распространять среди учащихся, предварительным их размножением средствами современных информационных технологий. При этом следует также отметить, что кабинеты черчения большинства школ имеют классные доски, части которых имеют такие разграфировки.
|
|
|
Рис. 3. «Бесконечная лестница», изображенная в изометрии. |
|
Рис 2. Фрагменты специально разграфированных листов для выполнения: а – изометрических и б – прямоугольных изображений. |
||
Далее учитель на разграфированном листе для выполнения изометрий, создаёт изображение «бесконечной лестницы» допуская, что количество ступенек в том или ином направлении, может быть каким угодно. Затем он получившееся изометрическое изображение копирует на большой лист, не имеющий разграфировки для представления учащимся в классе (Рис. 3).
В начале занятия учитель, обращая внимание учащихся на данное изображение, спрашивает, что они в нем видят. После некоторого кратковременного наблюдения, устного размышления, и в некоторых местах под влиянием учительского вмешательства, ученики приходят к общему мнению, что на этом рисунке изображена «бесконечная лестница».
Под сильным впечатлением увиденного, класс заметно оживает.
В то же время учитель спрашивает у учащихся: действительно ли на этом рисунке изображена бесконечная лестница?
Пока учащиеся заняты поиском подходящего ответа, учитель показывает им изометрическое изображение той же «бесконечной лестницы», лишь с той разницей, что оно здесь нарисовано на разграфинном листе (Рис. 4).
|
|
|
|
|
Рис. 4. Изометрия «бесконечной лестницы», выполненная на специально разграфированном листе. |
Рис. 5. План (горизонтальная проекция) «бесконечной лестницы». |
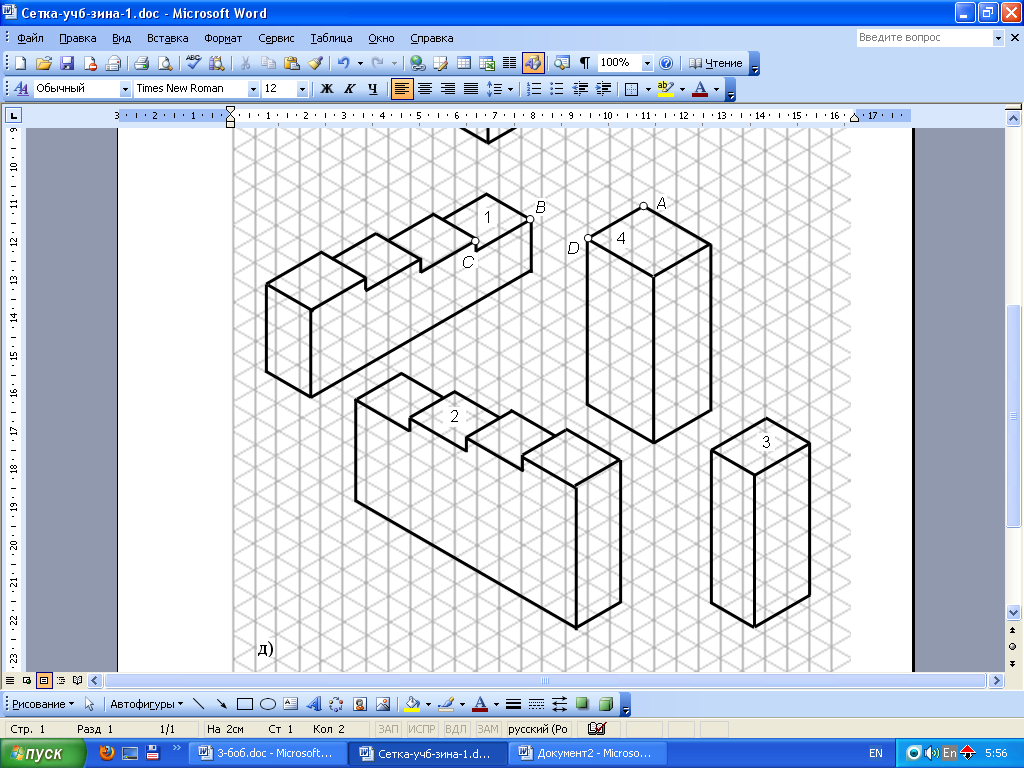
Рис.6. Изображения блоков, из которых можно собрать изометрию «бесконечной лестницы». |
Задание. Начертить план (горизонтальную проекцию) «бесконечной лестницы» на разграфированном квадратами листе (Рис. 2, б), приняв в качестве размеров элементов размеры квадратов, использовавшихся при выполнении ее изометрии (Рис. 4).
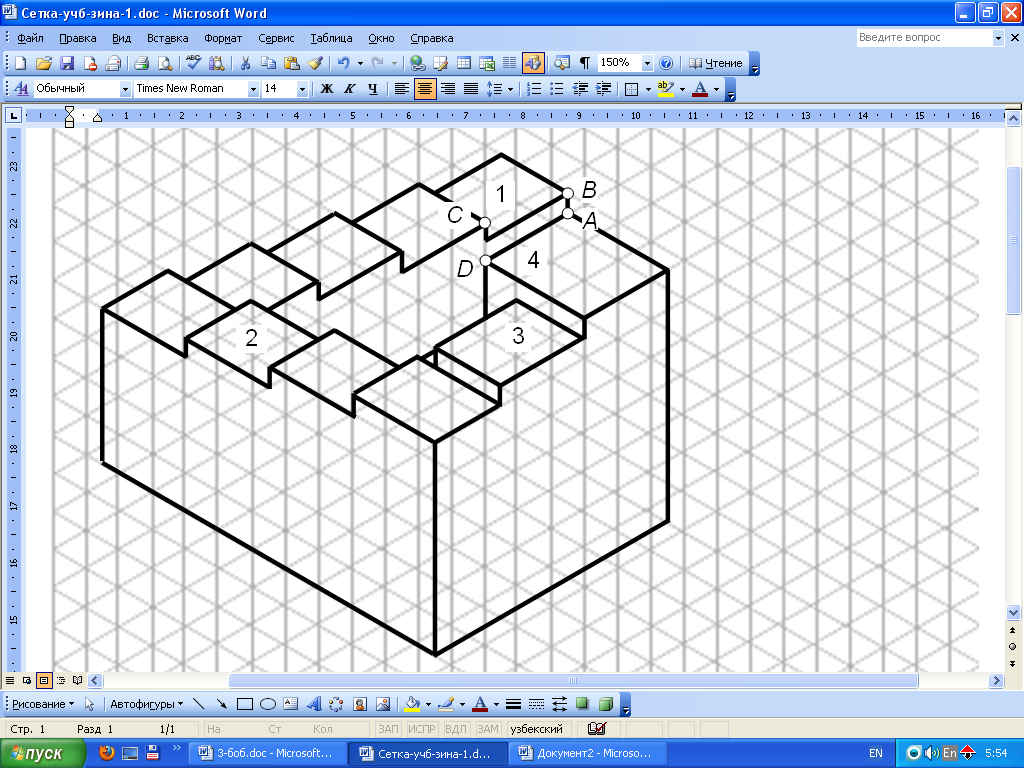
Решение задачи будет представлять собой, план (горизонтальную проекцию) объекта, приводимый на рис. 5.
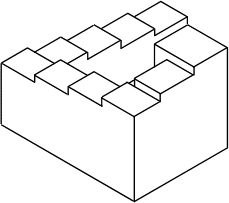
Секрет выглядывания изображенной на рис. 3 лестницы как бесконечной, раскрыт. Для того, чтобы четырехмаршовая лестница в изометрии выглядела как бесконечная, необходимо расположение ребра BC самой нижней ступеньки, находящейся на заднем плане – над ребром AD самой верхней ступеньки, находящегося на переднем плане. Причем прямые, проходящие через вершины А и В, и С и D этих ребер должны составлять с горизонтальной линией угол, равный 60&#; (Рис. 5).
На следующем этапе 1-го занятия, учащиеся «разбивают» изометрию лестницы (Рис. 4) на составные части, и еще глубже осознают причину выглядывания изображения обычной лестницы как бесконечной (Рис 6).
На 2-м занятии, проводимом на тему «Решение творческих графических задач с элементами проектирования» учащиеся займутся проектированием лестниц, изометрические проекции (технические рисунки) которых изображают «бесконечную лестницу», взяв по-разному, количество ступенек и их ширину.
На всем протяжении 2-х часового экспериментального занятия, проведенного нами на выше изложенном учебном материале, почти у всех учащихся класса наблюдалась заметная активность. Это требовало от нас более внимательного анализа моментов, специфичных к таким типам занятий, с целью дальнейшего их совершенствования.
В результате такого анализа выяснилось, что описанные нами выше экспериментальные занятия, целиком сходятся с занятиями, проведение которых рекомендуется педагогической технологией, называемой «Развитие критического мышления» [1] лишь с той разницей, что в этой технологии развитие критического мышления достигается через чтение и письмо, а у нас – через пространственное представление и техническое рисование.
Литература:
1. Стил, Ж., Мередис, К., Темпл, Ч. Основы развития критического мышления. Пособия: 1 – 8. – Бишкек, 1998.