- В данной работе рассматривается возможность повышения эффективности работы планировщика заданий кластерной системы при учете в процессе планирования способности пакетных заданий изменять число используемых ресурсов. В ходе работы сформирован ряд не эвристических алгоритмов, в том числе использующих механизм backfill, и проведено имитационное моделирование их работы при различных входных данных. Результаты моделирования показали повышение эффективности использования ресурсов до 25%.
- В настоящее время большое распространение получили кластерные
системы. Данные системы являются сложными программно-аппаратными
комплексами [1,2] одной из важнейших частей которых является
планировщик заданий. В большинстве случаев вычислительный кластер
используется для одновременного решения нескольких ресурсоемких
задач, каждая из которых требует определенный объем временных и
аппаратных ресурсов для совершения расчета. Планировщик заданий [3]
отвечает за распределение доступных кластерных ресурсов между
задачами. В случае превышения требованиями задач доступных ресурсов
кластера, они образуют очередь заданий, управляемую также
планировщиком заданий.
- Существует несколько широко применяемых алгоритмов планирования заданий. Самые простые алгоритмы принимают решение о выделении ресурсов основываясь на текущем состоянии очереди: когда на кластере освобождается достаточное число ресурсов, их занимает следующая задача. Простейший способ определения очередности дает алгоритм FIFO (First input first output). Следующая задача определяется по времени постановки в очередь. Другим примером является алгоритм SJF(smallest jobs first) и LJF(largest jobs first) [4]. Данные задачи выбирают очередную задачу согласно числу требуемых ресурсов. Наиболее часто применяется алгоритм обратного заполнения Backfill. Данный алгоритм использует данные не только о текущем состоянии очереди, но и проводит процесс планирования, определяя требования к ресурсам на протяжении определенного времени. Если результаты планирования показывают наличие свободных ресурсов, недостаточных для первоочередных заданий, то подключается процесс обратного заполнения: производится поиск задачи в очереди, подходящей по запросам к доступному объему ресурсов [5]. Поиск задачи также может проходить с использованием различных стратегий. Стратегия Best Fit производит поиск задачи максимально покрывающей доступные ресурсы, стратегия First Fit ищет ближайшую задачу способную поместиться в доступные ресурсы.
- Все вышеуказанные алгоритмы планируют размещения задач исходя из их двух основных критериев – объема запрашиваемых вычислительных ресурсов и времени счета. Данные критерии являются условными, поскольку большинство параллельных программ позволяют варьировать число используемых ресурсов, причем сокращение выделенных для расчетов узлов, ведет к увеличению времени счета. Такие задачи называют масштабируемыми или пластичными [6]. Согласно текущим исследованиям [7], более 80% параллельных задач являются масштабируемыми
- Существует несколько широко применяемых алгоритмов планирования заданий. Самые простые алгоритмы принимают решение о выделении ресурсов основываясь на текущем состоянии очереди: когда на кластере освобождается достаточное число ресурсов, их занимает следующая задача. Простейший способ определения очередности дает алгоритм FIFO (First input first output). Следующая задача определяется по времени постановки в очередь. Другим примером является алгоритм SJF(smallest jobs first) и LJF(largest jobs first) [4]. Данные задачи выбирают очередную задачу согласно числу требуемых ресурсов. Наиболее часто применяется алгоритм обратного заполнения Backfill. Данный алгоритм использует данные не только о текущем состоянии очереди, но и проводит процесс планирования, определяя требования к ресурсам на протяжении определенного времени. Если результаты планирования показывают наличие свободных ресурсов, недостаточных для первоочередных заданий, то подключается процесс обратного заполнения: производится поиск задачи в очереди, подходящей по запросам к доступному объему ресурсов [5]. Поиск задачи также может проходить с использованием различных стратегий. Стратегия Best Fit производит поиск задачи максимально покрывающей доступные ресурсы, стратегия First Fit ищет ближайшую задачу способную поместиться в доступные ресурсы.
- Для выбора и сравнения качества работы алгоритмов необходимо
определить способы их оценки.
- Главным критерием оценки работы алгоритмов планирования заданий является время завершения вычислений. Чем лучше алгоритм, тем раньше должны закончиться вычисления. Реальное время завершения Fr показывает время, когда закончила расчет последняя задача в очереди. С этого момента, все кластерные ресурсы становятся полностью доступными. Альтернативно существует оценка Fm – средневзвешенное время завершения последних задач. Эта оценка позволяет более точно отражать качество работы алгоритма в определенных ситуациях: предположим, что алгоритм планирования заданий качественно упаковал расчетное поле, но одна, требующая много времени и мало узлов задача, оказалась последней запущенной задачей. Тогда, на время работы этой задачи увеличится Fr, хотя значительная часть ресурсов кластера доступна для новых задач.
- Для оценки влияния динамических заданий на размерность задач используется оценка суммарного объема использованных ресурсов Ja. Она описывается как сумма использованных ресурсов каждой из задач. Уменьшение Ja относительно показателя для статических алгоритмов говорит о том, что для выполнения одного и того же набора задач потребовалось меньше вычислительных ресурсов, т.е. внутренние ресурсы использовались эффективнее.
- Другой важной характеристикой является эффективность использования вычислительных ресурсов. Эффективность использования ресурсов можно рассчитать как отношение использованных ресурсов к общему числу доступных ресурсов за время работы. Поскольку используется две оценки времени работы алгоритма, то и оценок эффективности две. Эффективность Er и Em рассчитываются по формуле 1 и 2 соответственно:
- Главным критерием оценки работы алгоритмов планирования заданий является время завершения вычислений. Чем лучше алгоритм, тем раньше должны закончиться вычисления. Реальное время завершения Fr показывает время, когда закончила расчет последняя задача в очереди. С этого момента, все кластерные ресурсы становятся полностью доступными. Альтернативно существует оценка Fm – средневзвешенное время завершения последних задач. Эта оценка позволяет более точно отражать качество работы алгоритма в определенных ситуациях: предположим, что алгоритм планирования заданий качественно упаковал расчетное поле, но одна, требующая много времени и мало узлов задача, оказалась последней запущенной задачей. Тогда, на время работы этой задачи увеличится Fr, хотя значительная часть ресурсов кластера доступна для новых задач.
|
1) |
|
|
2) |
- где N общее число узлов
- Особенностью данной группы алгоритмов является их способность
изменять объем требуемых вычислительных узлов и учитывать изменения
требуемого времени работы задачи.
- Существует большое число исследований на тему планирования заданий. В работе [8] приводится разработка алгоритма планирования масштабируемых заданий. Предложенный алгоритм основывается на задании векторов используемых ресурсов, времени исполнения и субъективной удовлетворенности пользователя. Данная характеристика учитывается в процессе планирования. Сам алгоритм строится на основе эвристических механизмов, которые в свою очередь требуют большой объем ресурсов для гарантированно качественного результата.
- В данной работе использован иной подход. Для каждой из прикладных программ в расчетной задаче задается модель, отвечающая за изменение времени вычисления при изменении используемых ресурсов. В данной работе была использована простейшая модель, построенная на основе закона Амдала. Также, каждая из задач включает пороговые значения изменения числа ресурсов. В реальной ситуации нижняя граница обычно зависит от необходимого объема памяти, а верхняя от максимальной точки эффективности. Увеличение числа ресурсов более этой точки не только не ведет к уменьшению времени счета, но может привести к его увеличению.
- Также в качестве метрики используется общая эффективность использования ресурсов относительно тестового алгоритма, а не произвольно заданная характеристика.
- Первый предложенный алгоритм (bfbfr) является вариацией алгоритма поиска обратного заполнения для Backfill. Данный алгоритм, подобно алгоритму Best Fit, пытается найти наилучшее заполнение для свободного окна. Разница в том, что поиск происходит с учетом возможного изменения размера задачи под заданное окно. Помимо списка влезающих заданий, в него добавляются все задания, влезающие в окно после изменения своего размера.
- Следующие два алгоритма (drf и dre) являются разряжающими и базируются на идее использования доступного окна соседними задачами и ориентированны на увеличение используемых задачей ресурсов. Если в определенный момент образовалось окно, то его могут занять запланированные на запуск задачи. Каждая задача получает часть ресурсов данного окна, а значит, сокращает время своей работы, делая старт следующих в очереди заданий более ранним. Разница между алгоритмами заключается в способе раздела окна между задачами. drf по возможности сохраняет соотношение ресурсов между задачами. Например, если одна задача требовала 4 узла, а вторая 2, то при появлении трех свободных узлов два достанутся первой, а однин второй. dre пытается максимально выровнять время работы программы за счет доступного окна. Задача, требующая больше всего времени получает в свое распоряжение дополнительные узлы. За счет этого сокращается время появления больших окон для следующих задач.
- Последние два алгоритма (drfn и dren) являются уплотняющими и пытаются добавить за счет свободного окна следующую задачу. Это приводит к росту времени расчета всех задач, но приводи к росту общей эффективности использования ресурсов. Данные алгоритмы ориентированны на уменьшение числа используемых задачей ресурсов. Если для следующей по очереди задачи требуется больше ресурсов чем доступно, то изменяется число ресурсов используемых ею и соседями по запуску. Алгоритмы также решают задачу разделения ресурсов различными способами. Drfn старается максимально сохранить соотношение используемых ресурсов, а dren пытается выровнять время завершения
- Существует большое число исследований на тему планирования заданий. В работе [8] приводится разработка алгоритма планирования масштабируемых заданий. Предложенный алгоритм основывается на задании векторов используемых ресурсов, времени исполнения и субъективной удовлетворенности пользователя. Данная характеристика учитывается в процессе планирования. Сам алгоритм строится на основе эвристических механизмов, которые в свою очередь требуют большой объем ресурсов для гарантированно качественного результата.
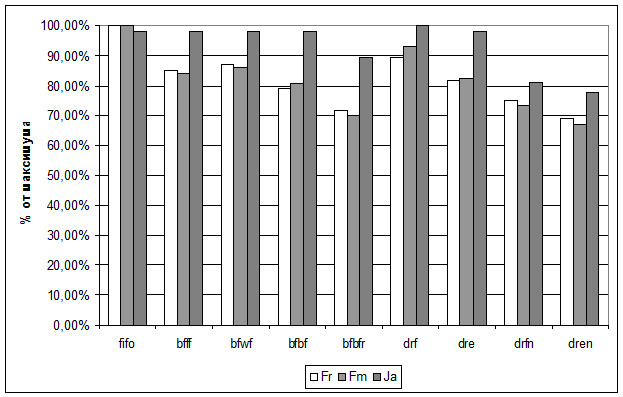
На рисунке представлены соотношения оценок для различных алгоритмов планирования, использованных для данных о реальной загрузке вычислительного кластера нашего института. Как вы можете заметить, что алгоритмы bfbfr и dren показали сокращение времени счета заданий на 25 процентов при этом исходя из характеристики Ja, алгоритм bfbfr лучше заполнил имеющиеся кластерные ресурсы, а dren использовал занятые ресурсы эффективнее.
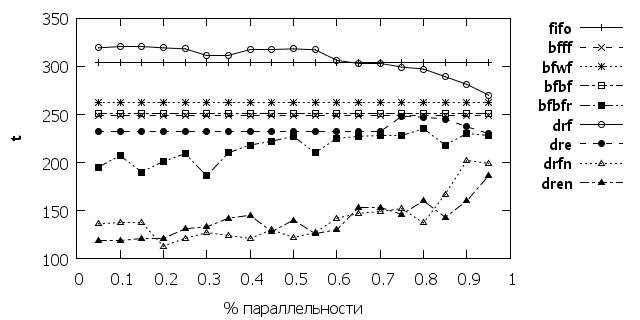
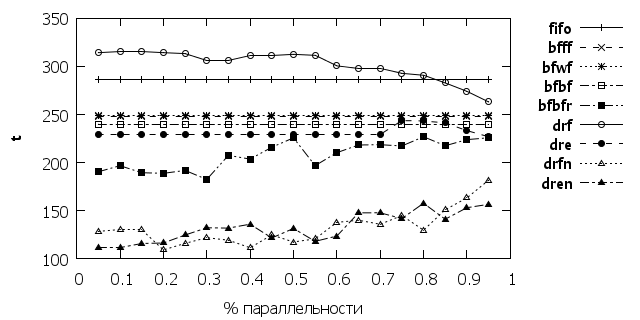
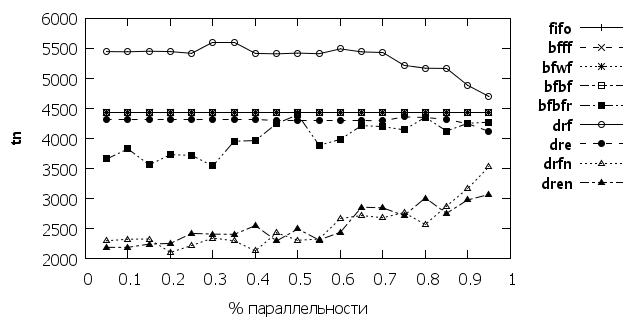
Интересные результаты видно на рис. 2-4. В данном случае постепенно изменялась степень параллельности программы. Если алгоритм bfbfr проявил стабильность в своих результатах, то алгоритм drf и drfn(dren) показали противоположные зависимости. По мере роста параллельности показатель drf снижается, то для алгоритмов drfn(dren) он наоборот растет. Это показывает как сильно выбор алгоритма зависит от особенностей используемых на кластере приложений.
|
|
|
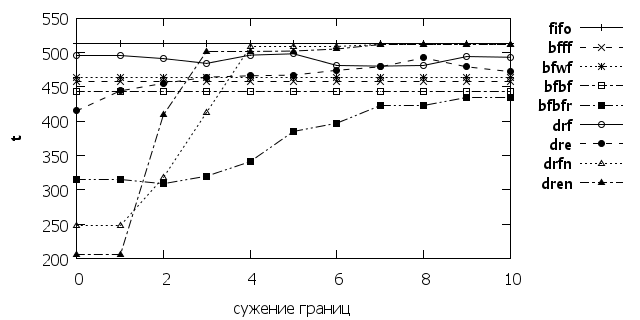
На рис. 5 и 6 представлены показатели для сужения границ масштабирования пластичных заданий. При значительном сужении границ, bfbfr остается единственным алгоритмом дающий превышающий классические алгоритмы результат.
|
|
- Необходимо развивать модель работы кластера. Должна учитываться
динамичность очереди заданий: появление и удаление заданий,
изменение приоритетов. Также необходимо учитывать недостоверность
получаемой информации о времени работы задания. Пользователи могут
заказывать значительно больше ресурсов, нежели потребуется для
расчета. Отдельно стоит отметить, что по ряду причин запуск задания
может завершиться сбоем (например, из-за не верных входных данных
или ошибки в программном обеспечении). Это приведет к практически
моментальному снятию задания. Достоверность запрашиваемых ресурсов
может различаться для конкретных программ.
- Отдельным объектом исследования является зависимость время работы программы от количества доступных узлов. Получение более точной информации позволит повысить точность результатов и надежность работы. Для возможности применения данного подхода в условиях реальной эксплуатации необходимо обеспечить поддержку специфичных возможностей изменения запрашиваемых ресурсов. Например, ряд программ могут требовать число узлов с целочисленным квадратным корнем (4,9,16..).
- Несмотря на то, что было рассмотрено несколько новых алгоритмов, необходимо продолжить исследование алгоритмов, комбинируя и дополняя их, с целью получения возможности нахождения наиболее оптимального алгоритма для определенного характера входных заданий и их параллельных приложений.
- Отдельным объектом исследования является зависимость время работы программы от количества доступных узлов. Получение более точной информации позволит повысить точность результатов и надежность работы. Для возможности применения данного подхода в условиях реальной эксплуатации необходимо обеспечить поддержку специфичных возможностей изменения запрашиваемых ресурсов. Например, ряд программ могут требовать число узлов с целочисленным квадратным корнем (4,9,16..).
- Полученные в ходе исследования алгоритмы показали в ряде случаев превосходство над классическими алгоритмами. Большое влияние на качество работы алгоритма показала способность прикладного программного пакета к масштабированию. Особенно интересно то, что на разные алгоритмы эта характеристика повлияла по разному. Для алгоритмов уплотнения к повышению эффективности ведут плохо масштабируемые задачи, в то время как для разряженных алгоритмов наоборот большую эффективность обеспечивают хорошо распараллеливаемые задачи. Это говорит о том, что для реализации качественного плана запуска необходимо учитывать, в том числе и возможность прикладного ПО к масштабированию.
- G. Hager, G. Wellein. «Introduction to High Performance Computing for Scientists and Engineers», CRC Press, 2010
- Воеводин В.В., Жуматий С.А., Вычислительное дело и кластерные системы. Изд-во: МГУ, 2007, 149 стр
- R. L. Henderson. Job scheduling under the portable batch system. In D. G. Feitelson and L. Rudolph, editors, Job Scheduling Strategies for Parallel Processing, volume 949 of LNCS, pages 279–294, 1995
- Saeed Iqbal, Rinku Gupta Yung-Chin Fang. Planning Considerations for Job Scheduling in HPC Clusters. Dell, 2005
- Maui Research Center, “Scheduling” 1998, http://anusf.anu.edu.au/~dbs900/PBS/Maui/scheduling.html
- Dror G. Feitelson, Larry Rudolph, Uwe Schwiegelshohn, Kenneth C. Sevcik, Kenneth C. Parkson Wong. Theory and practice in parallel job scheduling // Job Scheduling Strategies for Parallel Processing, Volume 1291, 1997, pp. 1–34, ISBN: 978-3-540-63574-1
- W. Cirne and F. Berman, “A model for moldable supercomputer jobs”. 15th Intl. Parallel & Distributed Processing Symp., Apr. 2001, http://www.lsd.dsc.ufpb.br/papers/moldability-model.pdf