Более 50 % средней ежедневной потребности воды (а это 132 л на человека) составляет не питьевая часть, которую можно заменить дождевой водой, если представить, что технические системы сбора атмосферных осадков, реализованные в индивидуальном порядке или даже для неширокого коллективного пользования будут повсеместно использоваться, то это обеспечит существенную экономию расходов питьевой воды.
Гипотеза исследования: объем дождевой воды может покрыть часть ежедневных расходов человека для хозяйственных нужд.
Цель работы: исследовать и изучить способы рационального использования дождевой воды.
Задачи: — изучить источники информации на предмет возможного объема сбора дождевой воды и характеристики дождевой воды;
– рассмотреть возможность сбора дождевой воды;
– рассмотреть способы применения дождевой воды в школе;
Дождевая вода — одна из форм атмосферных осадков. В условиях загрязненной атмосферы в дождевой воде растворяются оксиды азота и серы, пыль. При растворении в дождевой воде значительных количеств оксидов серы и азота выпадают кислотные дожди.
Очевидно, что чистота дождевой воды зависит от ряда факторов, а именно: санитарно-экологической обстановки территории, над которой образовалось облако, загрязнения атмосферы.
Для того чтобы оценить, сколько выпадет, или выпало влаги, применяется понятие «количество осадков».
Количество осадков — это высота слоя воды в миллиметрах, который образовался бы на поверхности земли, если бы она была абсолютно ровная, то есть осадки бы не стекали, не просачивались в почву и не испарялись. Количество осадков в миллиметрах численно равно массе воды, выпавшей на горизонтальную площадку в 1 квадратный метр.
Согласно данным [2] сайту наиболее дождливые периоды июнь, август, июль, когда выпадает до 34.04 мм осадков в среднем за 15 дождливых дней. В зимние месяцы и март осадков выпадает меньше, и месячная норма осадков составляет 14, 78 мм
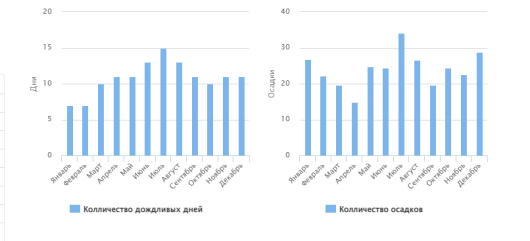
Рис. 1. Количество осадков и дождливых дней в течении года, г. Гусев Калининградская область
В менее дождливый месяц январе дней с осадками было 7, а количество осадков 26, 7 мм, таким образом за один дождливый день можно было собрать в среднем 3, 8 л воды на один квадратный метр или с среднем 0,89 л в сутки в январе.
В самый дождливый месяц — июль, выпадает 34 мм осадков за 15 дождливых дней, то есть в среднем 2, 26 литра воды на один квадратный метр за дождливые сутки или в среднем 1, 13 л в сутки в июле.
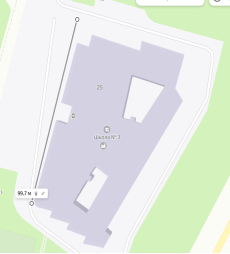
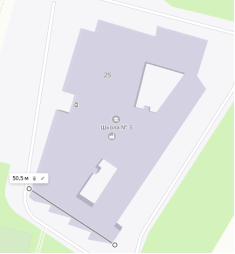
Рис. 2. Определение примерных размеров крыши школы, используя интернет-карты
Длина здания нашей школы около 99,7 метров, а ширина не менее 50,5 метров, с учетом внутренних дворов (9м x 21м и 21м х 10м), без учета покатости крыши, применив расчет площади:
5034,85–189–210=4635,85 (м 2 )
Мы выяснили что площадь крыши около 4635м 2
За самый не дождливый месяц — апрель, можно собрать около 70 000 литров дождевой воды, а в июле около 157 000 л дождевой воды.
Это с одной стороны большие объемы воды для хозяйственных нужд, но с другой стороны, эти объемы воды необходимо хранить.
На территории школы идет строительство теплицы, размером 6 м на 3 м, поверхность крыши с учетом покатости более 18 квадратных метров, в среднем в менее дождливый месяц можно собирать около 270 литров, а в летние до 600 л дождевой воды, для этого потребуется 3 бочки по 200 литров. Эту воду можно использовать в теплице для полива растений.
Минусом такого сбора может быть забивание листьями и другим растительным мусором стоков водоотвода, поэтому необходимо заранее предусмотреть его очистку.
Следует сделать вывод, что более 50 % средней ежедневной потребности воды составляет не питьевая часть, которую можно заменить дождевой водой, можно представить, что технические системы сбора атмосферных осадков, реализованные в индивидуальном порядке или даже для неширокого коллективного пользования, обеспечивают существенную экономию водных ресурсов. Гипотеза подтверждена, объемы дождевой воды действительно позволяют её использовать для хозяйственных нужд. Мы надеемся, что каждый человек в своем приусадебном хозяйстве, в быту начнет заботиться об экологической ситуации. Тогда и общая экологическая ситуация в мире начнет меняться.
Литература:
- Габриелян. Химия 7 класс. М., «Дрофа», 2000
- Каинов И. Н. Сборник элективных курсов по естествознанию. М, «Дрофа», 2002
- Погода г.Гусев Калининградская область. (Электронный ресурс)//. — https://pogoda.365c.ru/russia/gusev/po_mesyacam Физическая культура. Учебник для 8–9 классов под ред. В. И. Ляха. –М., «Просвящение», 2012
- Яндекс-карты. МАОУ «СОШ № 3» г.Гусев. (электронный ресурс).- https://yandex.ru/maps/-/CCU0mFtKhC







