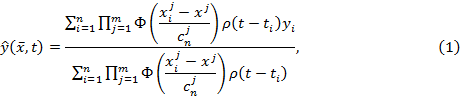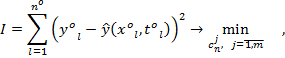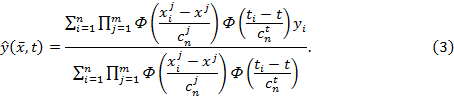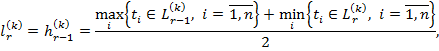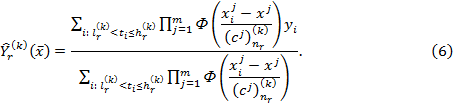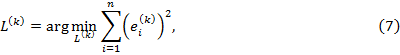Введение
На сегодняшний день теория идентификации в основном посвящена вопросам построения моделей стационарных объектов, что является, как правило, результатом некоторой идеализации. Реальные технические объекты имеют не постоянные, а изменяющиеся во времени параметры, т.е. являются нестационарными, что может быть следствием нестабильной работы или старения оборудования. Существенным для анализа нестационарных систем фактором является закон изменения параметров, который отражает характер и скорость их изменения. В данной работе рассматривается класс объектов с периодически изменяющимися параметрами.
Пусть при моделировании
исследователь располагает единственной реализацией выборки измерений
![]() ,
,
![]() ,
где
,
где
![]() –
i-е
измерение j-го
входа объекта,
–
i-е
измерение j-го
входа объекта,
![]() – i-е
измерение выхода объекта,
– i-е
измерение выхода объекта,
![]() – соответствующий момент времени. Параметры объекта изменяются
во времени с некоторой известной периодичностью, а время наблюдений
превышает этот период.
– соответствующий момент времени. Параметры объекта изменяются
во времени с некоторой известной периодичностью, а время наблюдений
превышает этот период.
В [1] для решения
поставленной задачи предлагается введение в непараметрическую оценку
регрессии функции памяти
![]() ,
позволяющей придавать «старой» информации меньший вес:
,
позволяющей придавать «старой» информации меньший вес:
где
![]() – ядерная функция,
– ядерная функция,
![]() –
параметр размытости, который удовлетворяет следующим свойствам:
–
параметр размытости, который удовлетворяет следующим свойствам:
Параметры размытости
![]() определяются
путем решения задачи минимизации квадратичного показателя
соответствия выхода объекта и выхода модели:
определяются
путем решения задачи минимизации квадратичного показателя
соответствия выхода объекта и выхода модели:
где
![]() ,
,
![]() –
выборка наблюдений, не участвующих в построении модели
–
выборка наблюдений, не участвующих в построении модели
![]() (экзаменующая выборка).
(экзаменующая выборка).
Одним из примеров
![]() может служить функция
может служить функция
также в качестве функции
памяти возможно использование ядерной функции
![]() :
:
Описание алгоритма
Идея предлагаемого в данной работе подхода основывается на том, что любой нестационарный объект на некотором конечном интервале можно описать стационарными моделями, тогда модель нестационарного объекта будет состоять из совокупности моделей стационарных интервалов, а задача будет сводиться к определению этих интервалов.
Введем понятие разбиения.
Разбиением
![]() на множестве
на множестве
![]() (
(![]() )
будем называть систему подмножеств, для которой выполняются условия:
)
будем называть систему подмножеств, для которой выполняются условия:
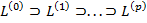 .
Каждое подмножество разбиения k-го
уровня является подмножеством некоторого подмножества разбиения
.
Каждое подмножество разбиения k-го
уровня является подмножеством некоторого подмножества разбиения
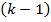 -го
уровня (
-го
уровня ( ).
).для
 справедливо
справедливо
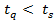 ,
,
 ,
,
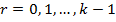 .
Подмножества разбиения k-го
уровня упорядочены по времени.
.
Подмножества разбиения k-го
уровня упорядочены по времени.
Каждому
подмножеству
![]() разбиения
разбиения
![]() поставим в соответствие две величины: начало (
поставим в соответствие две величины: начало (![]() )
и конец (
)
и конец (![]() )
временного интервала:
)
временного интервала:
По выборкам измерений,
компонента времени
![]() которых принадлежит множеству
которых принадлежит множеству
![]() ,
строится частная модель
,
строится частная модель
![]() ,
структура оценки поверхности регрессии имеет вид:
,
структура оценки поверхности регрессии имеет вид:
Класс частных моделей
![]() выбирается исследователем. Это может быть как структура
выбирается исследователем. Это может быть как структура
![]() ,
заданная с точностью до параметров
,
заданная с точностью до параметров
![]() :
:
Каждое разбиение производится из условия минимума суммы квадратов отклонений выхода модели от выхода объекта:
где регрессионные остатки
![]() определяются как:
определяются как:
Разбиение k-го
уровня при построении частных моделей в виде (6) и (5)
характеризуется
![]() и
и
![]() параметрами соответственно:
параметрами соответственно:
-![]() границ
интервалов (из них
границ
интервалов (из них
![]() граница известна из разбиения
граница известна из разбиения
![]() -го
уровня);
-го
уровня);
-
![]() )
параметров размытости на интервалах (
)
параметров размытости на интервалах (![]() параметров известны из разбиения
параметров известны из разбиения
![]() -го
уровня) для частных моделей вида (6) и
-го
уровня) для частных моделей вида (6) и
![]() параметров (
параметров (![]() параметров известно) для частных моделей вида (5).
параметров известно) для частных моделей вида (5).
Таким образом, оптимизация
квадратичного критерия (7) производится по
![]() и
и
![]() параметрам соответственно. При этом на стадии разбиения важным
является определение границы разбиения. Поэтому при выборе частных
моделей вида (6) в качестве приближенных оценок параметров размытости
будем использовать величину:
параметрам соответственно. При этом на стадии разбиения важным
является определение границы разбиения. Поэтому при выборе частных
моделей вида (6) в качестве приближенных оценок параметров размытости
будем использовать величину:
где
![]() – упорядоченные значения измерений входной величины
– упорядоченные значения измерений входной величины
![]() ,
компонента времени
,
компонента времени
![]() которых принадлежит множеству
которых принадлежит множеству
![]() .
Таким образом, оптимизация критерия (7) происходит по одному
параметру – границе разбиения, а параметры размытости
.
Таким образом, оптимизация критерия (7) происходит по одному
параметру – границе разбиения, а параметры размытости
![]() настраиваются после завершения процедуры разбиения.
настраиваются после завершения процедуры разбиения.
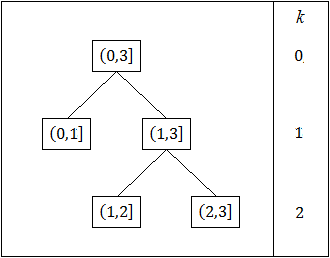
Процедура разбиения может быть представлена бинарным деревом, в котором каждая вершина характеризуется: временным интервалом, на котором строится частная модель, подмножеством наблюдений, принадлежащих этому интервалу, и самой частной моделью [2].
На основе анализа
информационных критериев было получено условие предпочтения разбиения
![]() разбиению
разбиению
![]() (условие остановки роста дерева):
(условие остановки роста дерева):
Данное условие можно интерпретировать, как требование к последующему разбиению быть значимо лучше предыдущего.
Закон распределения регрессионных остатков зависит от вида нестационарности и в общем случае не является нормальным, поэтому для проверки статистической гипотезы (8) предполагается использование критериев, устойчивых к отклонениям от нормальности, например, критерия Левене [3].
Во
избежание возможности построения модели по чрезмерно малому числу
наблюдений, введем величину
![]() ,
определяющую минимальное число точек, по которым может строиться
частная модель:
,
определяющую минимальное число точек, по которым может строиться
частная модель:
где
![]() – мощность множества
– мощность множества
![]() Пороговое
значение
Пороговое
значение
![]() выбирается на основе имеющейся априорной информации.
выбирается на основе имеющейся априорной информации.
Каждое
разбиение сокращает область поиска следующей границы разбиения
минимум на
![]() точек, а максимально возможное число разбиений:
точек, а максимально возможное число разбиений:
где
функция
![]() возвращает максимальное целое число, которое меньше аргумента
функции.
возвращает максимальное целое число, которое меньше аргумента
функции.
Численные исследования
С целью определения эффективности предложенного алгоритма были проведены численные исследования. Поведение объекта имитировалось уравнением
где
![]() – центрированная помеха, распределенная по нормальному закону,
уровень которой равен 5% от уровня основного сигнала. Входное
воздействие
– центрированная помеха, распределенная по нормальному закону,
уровень которой равен 5% от уровня основного сигнала. Входное
воздействие
![]() принадлежит интервалу от 0 до 1. Отсчеты по
принадлежит интервалу от 0 до 1. Отсчеты по
![]() равномерны (
равномерны (![]() ,
,
![]() ).
).
Исследование алгоритма (4)
и его сравнение с (1) и (3) производились при различных функциях
изменения параметра объекта
![]() (период изменения параметра объекта совпадает со временем
наблюдения): скорость изменения параметра
(период изменения параметра объекта совпадает со временем
наблюдения): скорость изменения параметра
![]() постоянна (см. Пример 1), скорость изменения параметра
постоянна (см. Пример 1), скорость изменения параметра
![]() непостоянна (см. Пример 2).
непостоянна (см. Пример 2).
За показатель качества
полученных оценок была выбрана среднеквадратическая ошибка
![]() где
где
![]() ,
,
![]() –
экзаменующая выборка,
–
экзаменующая выборка,
![]() –
полученная оценка регрессии в точке
–
полученная оценка регрессии в точке
![]() .
.
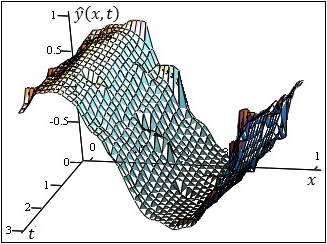
Пример 1.
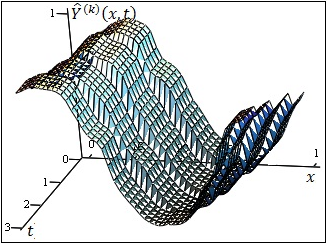
![]() истинная зависимость выхода
объекта от входного воздействия и времени представлена на Рис. 1.
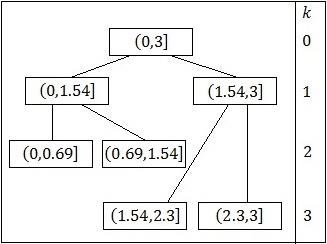
Частные модели строятся в виде (6). В результате применения процедуры
разбиения было получено 4 временных интервала (дерево разбиений
приведено на Рис. 2). На
Рис. 3 представлен набор частных моделей
истинная зависимость выхода
объекта от входного воздействия и времени представлена на Рис. 1.
Частные модели строятся в виде (6). В результате применения процедуры
разбиения было получено 4 временных интервала (дерево разбиений
приведено на Рис. 2). На
Рис. 3 представлен набор частных моделей
![]() (
(![]() ),
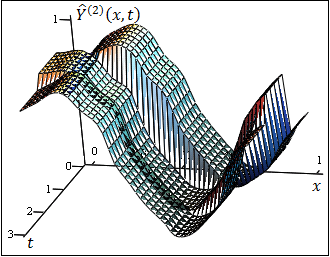
на Рис. 4 –
модель нестационарного объекта вида (1) с функцией памяти вида (2)
(
),
на Рис. 4 –
модель нестационарного объекта вида (1) с функцией памяти вида (2)
(![]() ).
Среднеквадратическая ошибка при построении модели вида (3) составляет
).
Среднеквадратическая ошибка при построении модели вида (3) составляет
![]() .
.
-
Рисунок 1. Зависимость выхода объекта от входного воздействия и времени
Рисунок 2. Дерево регрессии
-
Рисунок 3. Частные модели разбиения 3-го уровня
Рисунок 4. Модифицированная непараметрическая оценка функции регрессии (1)
С
уменьшением скорости изменения параметра
![]() сокращается число интервалов разбиения, а также происходит уменьшение
значения среднеквадратической ошибки, как при построении модели,
представляющей собой набор частных моделей, так и при построении
модели вида (1) с функцией памяти вида (2) и модели вида (3).
сокращается число интервалов разбиения, а также происходит уменьшение
значения среднеквадратической ошибки, как при построении модели,
представляющей собой набор частных моделей, так и при построении
модели вида (1) с функцией памяти вида (2) и модели вида (3).
Результаты численных
исследований показали, что при равномерном изменении параметров
объекта во времени значения выбранного показателя качества модели
вида (4) и модели вида (3) соизмеримы. Одновременно с этим,
построение модели, состоящей из совокупности частных моделей вида
(6), позволяет упростить решение задачи настройки параметров
размытости за счет того, что вместо одной модели с
![]() параметром размытости строятся
параметром размытости строятся
![]() моделей с
моделей с
![]() параметрами. Модифицированная оценка регрессии (1) с функцией памяти,
не имеющей настраиваемых параметров, является альтернативным способом
снижения числа параметров, по которым производится оптимизация.
Вследствие того, что функция памяти одинакова для объектов, параметры
которых изменяются по разным законам и с разной скоростью, значения
показателя среднеквадратической ошибки таких моделей превышает
аналогичные показатели моделей вида (3) и (4).
параметрами. Модифицированная оценка регрессии (1) с функцией памяти,
не имеющей настраиваемых параметров, является альтернативным способом
снижения числа параметров, по которым производится оптимизация.
Вследствие того, что функция памяти одинакова для объектов, параметры
которых изменяются по разным законам и с разной скоростью, значения
показателя среднеквадратической ошибки таких моделей превышает
аналогичные показатели моделей вида (3) и (4).
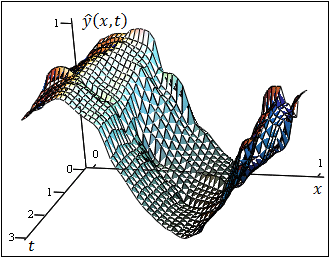
Пример 2.
![]() ,
на Рис. 5 представлена истинная зависимость выхода объекта от
входного воздействия и времени. Условие остановки процедуры разбиения
было выполнено после 2-го разбиения (на Рис. 6 показано дерево
разбиений). Набор
частных моделей
,
на Рис. 5 представлена истинная зависимость выхода объекта от
входного воздействия и времени. Условие остановки процедуры разбиения
было выполнено после 2-го разбиения (на Рис. 6 показано дерево
разбиений). Набор
частных моделей
![]() представлен на Рис. 7 (
представлен на Рис. 7 (![]() ),
на Рис. 8 –
модель нестационарного объекта вида (1) с функцией памяти вида (2)
(
),
на Рис. 8 –
модель нестационарного объекта вида (1) с функцией памяти вида (2)
(![]() ).
Среднеквадратическая ошибка при построении модели вида (3) составляет
).
Среднеквадратическая ошибка при построении модели вида (3) составляет
![]() .
.
-
Рисунок 5. Зависимость выхода объекта от входного воздействия и времени
Рисунок 6. Дерево регрессии
-
Рисунок 7. Частные модели разбиения 2-го уровня
Рисунок 8. Модифицированная непараметрическая оценка функции регрессии (1)
Результаты численных исследований показали, что при неравномерных изменениях параметров объекта во времени, а в особенности при наличии областей, в которых изменение параметров мало, предлагаемая оценка является более эффективной.
Заключение
В данной работе предложен способ восстановления нестационарной стохастической зависимости, основанный на рекуррентном разбиении временной области на квазистационарные интервалы, на которых производится построение частных моделей. Исключение времени из числа факторов, влияющих на выход каждой частной модели, позволяет сократить количество настраиваемых параметров.
Результаты могут быть распространены на динамические стохастические объекты.
Литература:
Медведев А.В., Фаустов А.В. О непараметрической оценке нестационарной функции регрессии по наблюдениям. / А.В. Медведев, А.В. Фаустов // Вестник Сибирского государственного аэрокосмического университета имени академика М.Ф. Решетнева: Сб. науч. тр.; СибГАУ. – Вып. 5. – Красноярск, 2010.
Hardle W. Applied Nonparametric Regression // Institut fur statistic and okonometrie, Berlin, 1994.
Levene H. Robust tests for equality of variances. // In I. Olkin and others (Eds): Contributions to probability and Statistics. Essays in Honor of Harold Hotelling. Stanford. – 1960. – pp. 278-292.