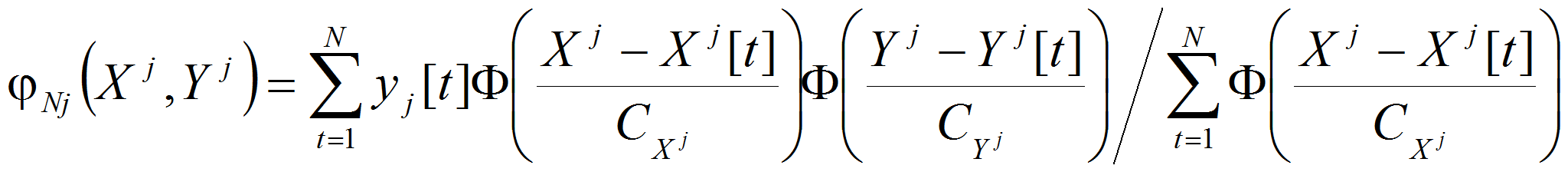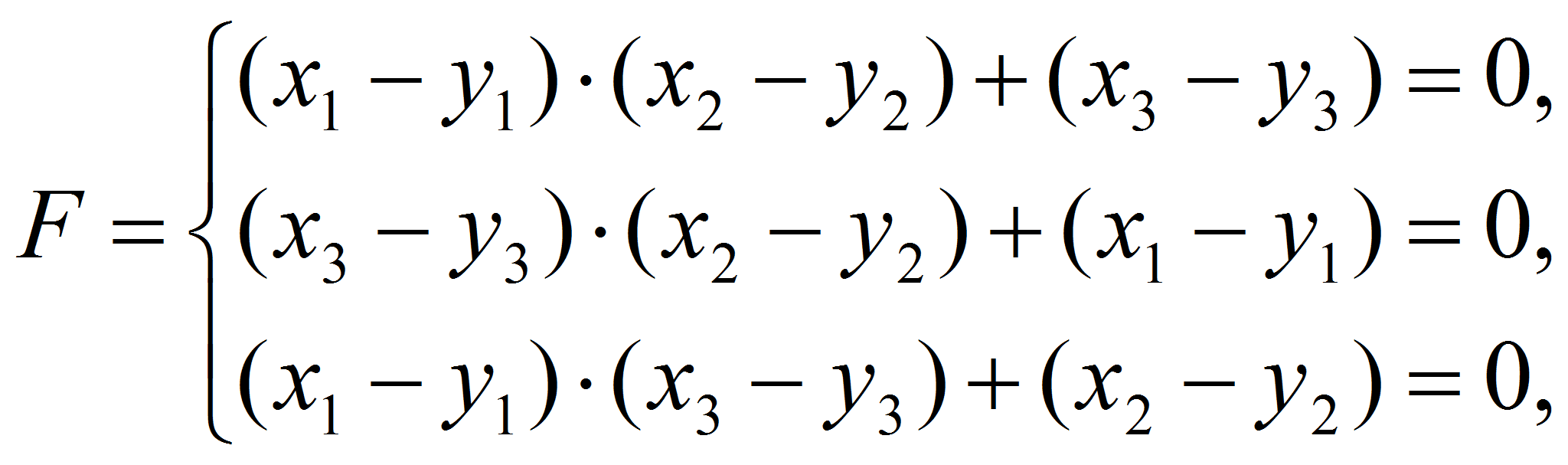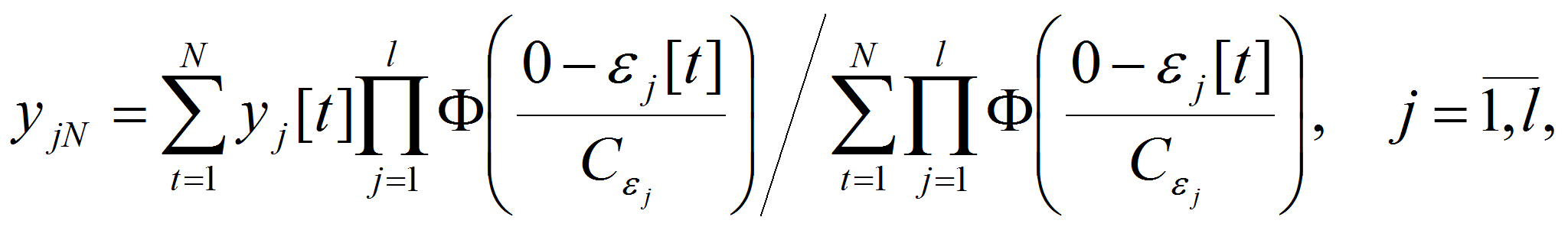Исследование алгоритма прогноза выхода комбинированной многосвязной системы

В повседневной жизни можно часто наблюдать существование таких систем, поведение, функционирование которых невозможно (в силу сложности самой системы или ее элементов) описать привычными математическими выражениями. Тем не менее, такая потребность возникает довольно часто, а тратить годы на то, чтобы разобраться во всевозможных запутанных цепочках, выявить и учесть все факторы, влияние которых может иметь хоть какое-то значение для построения модели, ждать появления новых измерительных комплексов для получения достоверных и надежных данных – нет возможности. Наряду с этим на практике распространен случай, когда часть связей подчиняются известным физическим, химическим и прочим законам, а часть имеют только качественное описание. Объекты исследования представляют собой процессы, имеющие непрерывный характер и сложную, технологическую жесткую структуру взаимных связей. Существующая структурная схема технологических связей между переменными самого объекта и его функциональных частей приводит к понятию многосвязности переменных, когда часть входных переменных одних объектов является входными для других в технологической цепочке. Это обстоятельство приводит к тому, что исследуемый класс объектов описывается не в традиционной форме «вход – оператор связи – выход», а неявно, в виде некоторой системы уравнений, определяющих соответствующие неявные функции.

1. Моделирование комбинированных многосвязных систем. Очень часто при наблюдении реального процесса исследователь сталкивается с ситуацией полного отсутствия информации о виде внутренних зависимостей и вследствие большой трудоемкости получения параметрической структуры его математической модели. Тем не менее, модель необходима, и получить ее нужно каким-либо способом. Первый путь – пытаться находить структуру так называемым «методом тыка», перебирая различные варианты, пытаясь найти тот, который приведет к лучшему описанию процесса. Второй – отказаться от этапа выбора структуры (к слову, в большинстве случаев самого трудоемкого и длительного) и, опираясь только на ту информацию, которой мы располагаем, построить непараметрическую модель процесса [4].

Рассмотрим теперь другой крайний случай, когда исследователь обладает полной информацией. Многие процессы могут быть описаны уравнениями физики или химии, например, уравнение теплового баланса или закон сохранения энергии. В таком случае глупо отказываться от имеющейся информации и вновь изобретать велосипед. Казалось бы, здесь все элементарно – выбираем подходящее описание и работаем с ним (настраиваем неизвестные параметры, усложняем структуру при необходимости).

Другой вопрос – как быть, если интересующий нас система объединяет в себе оба вышерассмотренных случая, то есть часть объектов системы могут быть описаны параметрически, а часть, в силу того, что нет информации о структуре, целесообразнее описывать, используя непараметрические методы моделирования. Модели процессов, которые строятся в условиях, когда априорная информация об исследуемом объекте имеет некий смешанный характер и может одновременно принадлежать нескольким уровням, будем называть комбинированными математическими моделями.

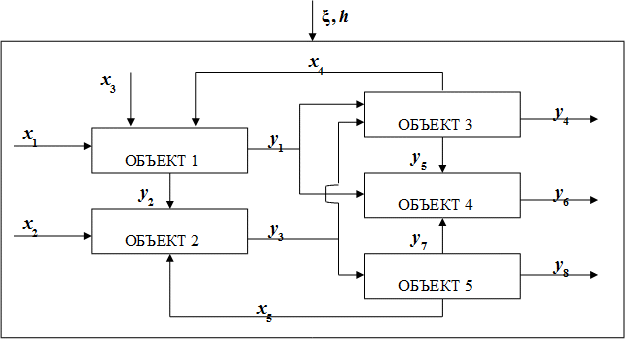
Многосвязным же будем называть объект, который описывается некоторой системой неявных функций от входных и выходных переменных. Условная блок схема представлена на рисунке 1. Это могут быть агрегаты внутри цеха, совокупность цехов на предприятии, предприятия, объединенные в производственные комплексы и прочее.

Рисунок 1. Условная блок-схема многосвязного объекта

На рисунке приняты следующие обозначения: x_i , i = 1,…,5 – входные переменные и приведенные к ним; y_i , i = 1,…,8 – выходные переменные (и приведенные к ним); ξ, h – случайные помехи с нулевым математическим ожиданием и ограниченной дисперсией, действующие на объекты и в каналах измерения.

Как видно, наличие обратных связей приводит к тому, что некоторая часть компонент вектора выхода зависит от других его компонент. Отметим, что такая ситуация типична для производственных комплексов с непрерывным характером технологического процесса. Часть соотношений, описывающих внутренние связи между входными и выходными переменными, на основе априорных сведений (например, законов сохранения, физико-химических закономерностей и так далее) может быть задана полностью или может быть представлена с точностью до набора параметров. Другая часть этих соотношений неизвестна, из-за недостатка информации она не может быть представлена с точностью до набора параметров и задается качественным образом с точностью до переменных. Проблема заключается в том, как в общей модели системы совместить разные уровни априорной информации о процессах, происходящих внутри нее, и одновременно учесть связи между объектами, приводящие к наличию неявных функций.

Сформулируем задачу. Пусть для многомерного статического объекта, подверженного действию неконтролируемых возмущений, со случайными ошибками, имеющими нулевое математическое ожидание и ограниченную дисперсию, могут быть проведены наблюдения вектора состояний . Плотности вероятностей величин X и Y неизвестны, но существуют для и , являющихся элементами некоторых замкнутых ограниченных областей в соответствующих пространствах, причем . Известно, что переменные на объекте связаны некоторыми соотношениями, часть из которых известна полностью, другая часть известна с точностью до набора параметров, а часть в силу недостатка априорной информации о структуре не может быть параметризована и представлена только некоторыми качественными соотношениями вход – выход.

Тогда, имея выборку наблюдений , требуется найти такое значение выходной величины , которое соответствует заданному входному воздействию – то есть осуществить прогноз выхода системы по заданному входному воздействию.

В данной работе будем рассматривать класс нелинейных статических объектов. В соответствии с этим, представим модель системы в следующем виде [2]

(1)

где

(2)

– непараметрические оценки качественных зависимостей по наблюдениям вектора состояний объекта.

Для получения прогноза в интересующей нас точке необходимо решить систему (1) при заданном входном воздействии . Рассмотрим метод, который позволяет получать прогноз выхода комбинированных многосвязных систем и учитывать при этом то, что система представлена неявными функциями.

2. Базовый алгоритм прогноза. На первом этапе была получена модель исследуемой системы в виде (1). Далее нам необходимо найти решение системы в заданной прогнозной точке – зная модель системы, всего-навсего нужно ее использовать для получения прогноза при известном входном воздействии. Но тут мы сталкиваемся с высокой сложностью решения, из которой вытекают, как минимум, две проблемы. Первая – недостаточная точность получаемого решения. Вторая – трудоемкость настройки параметров размытости самой модели. Остановимся на каждой из проблем более детально.

Существуют различные численные методы решения систем нелинейных уравнений (метод простых итераций, метод Ньютона, метод Бройдена) [1]. Все они являются достаточно трудоемкими в реализации, особенно в случае высоких порядков систем. Изначально указанная необходимость решения системы нелинейных уравнений возникла на этапе генерации выборки – когда для каждой точки входа, имея математическую имитационную модель, нужно было получить выходные значения системы. В качестве системы была выбрана следующая:

(3)

На то, чтобы найти решение данной нелинейной системы третьего порядка в одной точке методом простых итераций, требовалось около десяти секунд машинного времени. При этом заданная точность не достигалась, что, в свою очередь, приводило к ошибкам прогноза – неточные выборочные данные давали ошибки на этапе построения модели, а неверная модель приводила к ошибкам прогноза. Для достижения необходимой точности приходилось использовать более сложные методы, в частности, метод Бройдена, что вело к увеличению машинного времени, необходимого для нахождения решения в одной точке, до минуты. Кроме того, возникала проблема неоднозначности корня, что приводило к необходимости использования мультистартового поиска или метода Ляпунова. Но, на наш взгляд, это слишком высокая цена – работа программы уже на этапе генерации выборки занимала бы часы (в зависимости от требуемого объема выборочных данных), а решение системы требовалось бы также на этапе прогноза, где система за счет введения непараметрических конструкций вида (2) оказывалась еще более сложной. Но даже если допустить возможность использования такого подхода для получения прогноза, нам приходится столкнуться со второй проблемой, которая оказалась еще более сложной.

Дело в том, что настройка непараметрической модели сводится к настройке ее параметров – параметров размытости, которая осуществляется согласно выбранного критерия качества, например, среднеквадратичного [4]. Теперь представим себе, как это происходит. Выбранная система (3) третьего порядка включает шесть входных переменных и три выходных. Таким образом, максимальный порядок пространства оптимизации оказывается восьмым. В восьмимерной пространстве необходимо для каждого набора параметров, выбранных в соответствии с оптимизационной процедурой, в каждой из точек выборки найти решение системы – посчитать значение критерия. Таким образом, если объем выборки равен хотя бы тремстам, для настройки параметров размытости приходится находить решение системы 300m раз, где m – это число точек поискового пространства, в которых вычисляется значение функционала качества. Работа программы при этом занимала неприемлемо много времени (даже для выборки объемом сто, счет происходил более получаса). А это система всего-навсего третьего порядка.

Проблема получения качественных данных на этапе генерации была решена использованием системы специального вида

(4)

которая не только позволила избежать необходимости решения нелинейной системы на этапе генерации выборки, но и обеспечила существование единственного изолированного корня (доказательство этого весьма простое и в данной работе не приводится).

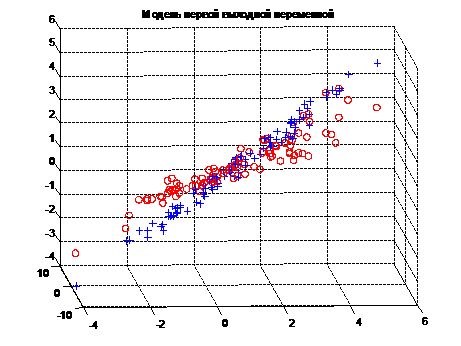
Тем не менее, вопрос получения качественной модели оставался открытым. Сложность в настройке параметров размытости требовала максимального упрощения и отказа от оптимизационных процедур. Рассматривалось максимально небольшое число точек пространства, что приводило к некачественной настройке модели и, в свою очередь, вело к недопустимым погрешностям в прогнозе (рисунок 3).

Рисунок 2. Пример расхождения модели с выборочными данными

Таким образом, стандартный подход, использующий решение системы нелинейных уравнений, в данной задаче оказался неприменим.

В качестве оценки решения замкнутых алгебраических систем нелинейных уравнений (1) было решено использовать непараметрическую статистику, которая бы позволяла работать не с решением систем, а с отклонением системы от нуля [2]

(5)

где – некоторая рабочая выборка невязок системы (1), специальным образом сгенерированная на основе исходной выборки «вход – выход», а именно

(6)

где – компоненты соответствующих вектор-функций.

Использование непараметрической статистики (5) при получении прогноза позволяет, во-первых, избежать сложности решения нелинейных систем, а во-вторых, учесть их многосвязность.

3. Исследование базового алгоритма прогноза методом статистического моделирования. В качестве объекта моделирования была выбрана система пятого порядка специального вида, аналогичная описанной ранее системе (4):

(7)

Первоначально была исследована зависимость ошибки прогноза от так называемой «степени неопределенности системы» - числа непараметризованных уравнений в системе. Поочередно каждое из уравнений системы (7) заменялось непараметрической оценкой типа (2), при этом ранее замененные также считались качественно определенными. Таким образом, система рассматривалась от полностью известной до полностью непараметризованной. Данные экспериментов сведены в таблицу 1 (лучшее значение по каждому случаю выделено курсивом). Под ошибкой прогноза здесь понимается суммарное абсолютное отклонение по всем компонентам выхода.

Таблица 1

Влияние степени неопределенности системы на ошибку прогноза

По данным таблицы 1 достаточно сложно сделать какой-то вывод о влиянии степени неопределенности системы на работоспособность алгоритма (прослеживается лишь увеличение машинного времени при увеличении числа непараметризованных уравнений в системе) – явной тенденции ухудшения или улучшения качества прогноза при разной степени неопределенности не наблюдается. Поэтому было решено воспользоваться дополнительным статистическим анализом данных.

Значение ошибки прогноза для каждого случая может рассматриваться как случайная величина, а ошибка прогноза, полученная в одном эксперименте – как реализация этой случайной величины. Таким образом, имеем пять независимых выборок по десять измерений в каждой. Для выявления влияния степени неопределенности предлагается проверить гипотезу однородности, а в качестве конкурирующей гипотезы рассмотреть гипотезу неоднородности [3]. Если основная гипотеза принимается, то можно с определенной уверенностью (выбранный уровень значимости) сделать вывод о том, что степень неопределенности не оказывает существенного влияния на работоспособность рассматриваемого алгоритма прогноза. Если основная гипотеза однородности отвергается, следует определить, в каком из пяти случаев результаты наилучшие, в каком наихудшие, и, если возможно, обнаружить тенденцию (для этих целей в качестве конкурирующей гипотезы можно использовать гипотезу доминирования, при этом статистически большая случайная величина будет соответствовать случаю худшего прогноза, и наоборот). Следует также отметить, что законы распределения неизвестны, в соответствии с этим предлагается производить проверку однородности независимых выборок, используя непараметрические тесты, в частности, критерий Крускала-Уоллиса и медианный тест [3]. Согласно обоим тестам, гипотеза об однородности нескольких независимых выборок подтвердилась, а, следовательно, можно заключить, что работоспособность алгоритма не зависит от степени неопределенности системы. Однако обратим внимание, что данный результат был получен в случае отсутствия помехи. Влияние помехи на непараметрические алгоритмы доказывалась неоднократно [4]. Значительная помеха, являясь причиной ухудшения непараметрической оценки, может сказываться на точности прогноза. В таком случае, степень неопределенности будет иметь прямое влияние на ошибку прогноза.

Следующим этапом проверки работоспособности алгоритма стало исследование зависимости точности получаемого прогноза от объема выборочных данных. Этот момент весьма актуален, поскольку, как уже указывалось ранее, высокая размерность задачи требует, в общем случае, выборок большого объема, что не только трудно достижимо по причине трудозатратности, дороговизны экспериментов и длительности получения данных (проблема нестационарности процессов), но и весьма трудоемко в обработке и требует значительного времени для осуществления расчетов и получения конечного результата. В связи с этим желательным моментом была бы относительная независимость точности прогноза от объема выборочных данных. Зависимость ошибки прогноза от объема выборочных данных представлена в таблице 2.

Таблица 2

Зависимость ошибки прогноза выхода от объема выборочных данных

По данным таблицы 2 можно сделать вывод о том, что в случае отсутствия помехи наблюдается тенденция повышения точности прогноза с ростом объема выборочных данных (по критерию Крускала–Уоллиса и по медианному тесту выборки признаны неоднородными). Однако, интерес вызвало увеличение (хотя и незначительное) средней ошибки при увеличении объема выборки с четырехсот до пятисот. Данное обстоятельство нелогично, поэтому единственным разумным объяснением этому могла служить однородность указанных выборок, на что указывало лишь незначительное изменение средней ошибки, – таком случае, увеличение можно было бы списать на случайность. Таким образом, было решено провести дополнительную проверку гипотезы об однородности двух независимых выборок по критерию Манна-Уитни [3]. Гипотеза об однородности указанных выборок подтвердилась с большой долей вероятности.

Наконец, рассмотрим зависимость предлагаемого алгоритма прогноза от величины аддитивной помехи, действующей в каналах измерения. В данном случае помеху будем вводить не в процентном соотношении к величине полезного сигнала, а по среднеквадратичному отклонению от точки, в которой дается прогноз (напомним, что использована система специального вида, которая обращается в ноль при равенстве входных и соответствующих выходных сигналов). Приведем конкретные числовые значения для входного и соответствующего ему выходного сигналов при разном уровне помех, для того чтобы наглядно продемонстрировать величину отклонения. Так, для помехи 0,001 при входном значении 0,1748 выходное было равно 0,1710; для помехи 0,01 эти значения соответственно равны 0,3139 и -0,2519; для помехи 0,05: -0,5866 и -0,7640; для помехи 0,1: 0,0238 и 0,4896; для помехи 0,2: 0,2296 и 0,9968; для помехи 0,5: 0,4365 и 2,9870; для помехи 1: -0.3391 и 4.7863. Результаты экспериментов приведены в таблице 3.

Таблица 3

Влияние уровня помехи на ошибку прогноза выхода системы

По данным таблицы 3 можно сделать вывод о том, что с ростом величины помехи прогноз выхода ухудшается, что вполне естественно. При этом стоит отметить, что даже при больших помехах суммарная ошибка прогнозных значений компонент вектора выхода оказывала весьма приемлемой (не превышала 0.5), то есть в среднем отклонение по компоненте было не больше 0.1 – что считается хорошим результатом, особенно учитывая те неточности измерения, которые вводились наличием помехи. В целом, относительно данного пункта можно сделать вывод о том, что алгоритм представляется нам достаточно нечувствительным к помехам, что является его плюсом.

Таким образом, в ходе экспериментов было установлено, что основным фактором, влияющим на работоспособность предлагаемого метода определения порядка, является объем выборочных данных, при этом влияние помехи на работу алгоритма менее значительно. Учитывая этот факт, можно предположить, что степень неопределенности системы на работоспособность алгоритма также большого влияния не имеет. Стоит отметить, что фактор объема выборочных данных является для рассматриваемого алгоритма противоречивым – с одной стороны для получения точного прогноза требуется большое число измерений, с другой – это приводит к долгой работе алгоритма. В то время как помехи и степень неопределенности системы столь существенного влияния на временной фактор не оказывают.

Заключение. В работе был рассмотрен случай, когда наличие обратных связей в системе приводит к тому, что некоторая часть компонент вектора выхода зависит от других его компонент. При этом часть соотношений, описывающих внутренние связи между входными и выходными переменными, на основе априорных сведений (например, законов сохранения, физико-химических закономерностей) может быть задана полностью. Другая часть этих соотношений неизвестна, из-за недостатка информации она не может быть представлена с точностью до набора параметров и задается качественным образом с точностью до переменных. Сложностью данной ситуации, наряду с сочетанием априорной информации разных уровней, является нелинейный характер зависимостей, а также то, что уравнения системы в силу многосвязности представляют собой неявные функции. Для получения прогноза в таком случае предлагается использование непараметрического подхода, базирующегося на нахождении отклонений модели системы от нуля.

Открытыми остались вопросы не единственности решения многосвязной системы, а также наличия неточностей в параметрической и непараметрической частях модели. Кроме того нерешенной осталась проблема сложности вычислений, что предполагает возможность создания различных модификаций алгоритма.

Литература:

1. Вержбицкий В. М. Численные методы (линейная алгебра и нелинейные уравнения): Учеб. пособие для вузов / В. М. Вержбицкий. – 2-е изд, испр. – М.: ООО «Издательский дом «ОНИКС 21 век», 2005. – 432 с.

2. Красноштанов А. П. Комбинированные многосвязные системы / А. П. Красноштанов. – Новосибирск: Наука, 2001. – 176 с.

3. Лагутин М. Б. Наглядная математическая статистика: Учеб. пособие / М. Б. Лагутин. – М.: БИНОМ. Лаборатория знаний, 2007. – 427 с.

4. Шестернева О. В., Мальцева Т. В. О выборе параметрической модели в задаче непараметрической идентификации // Материалы журнала «Вестник СибГАУ», 2010, C. 187 – 193.