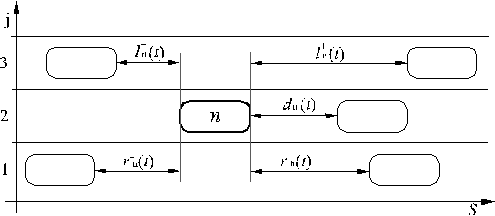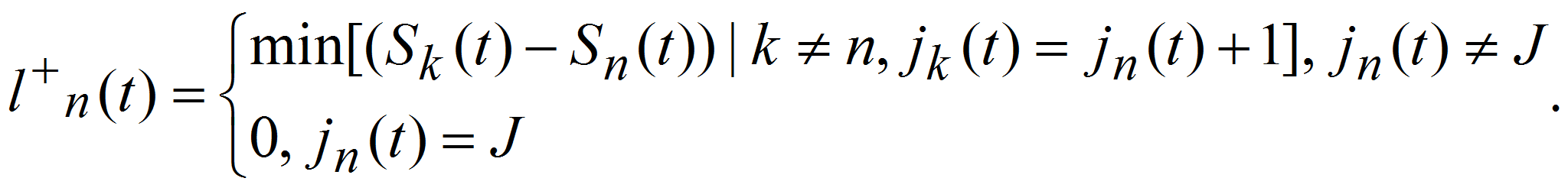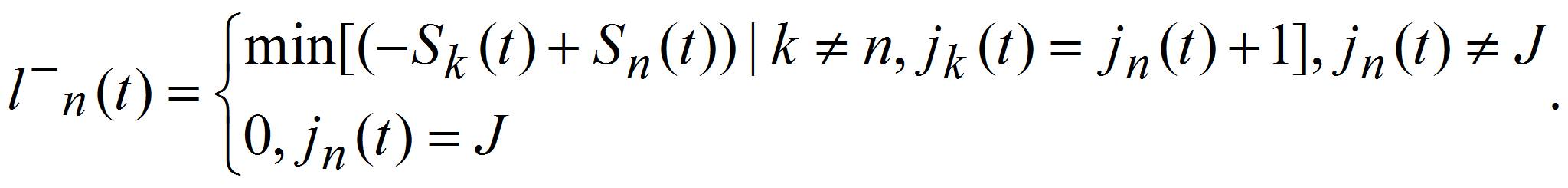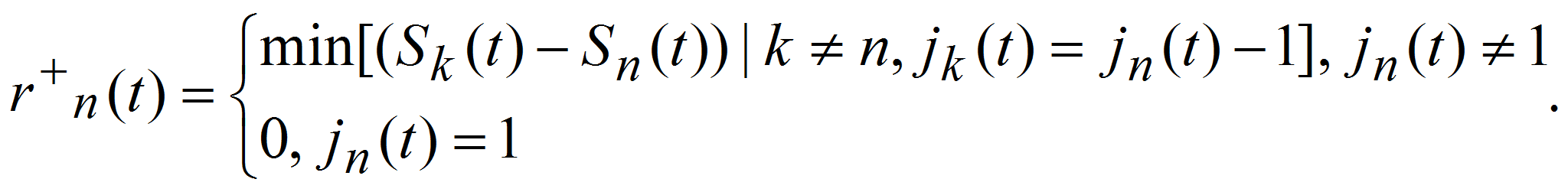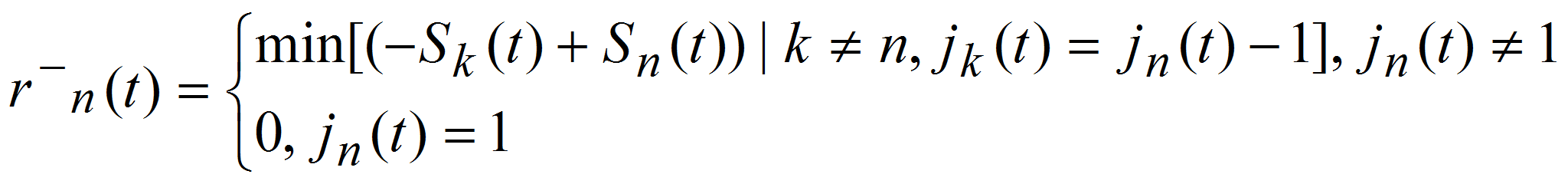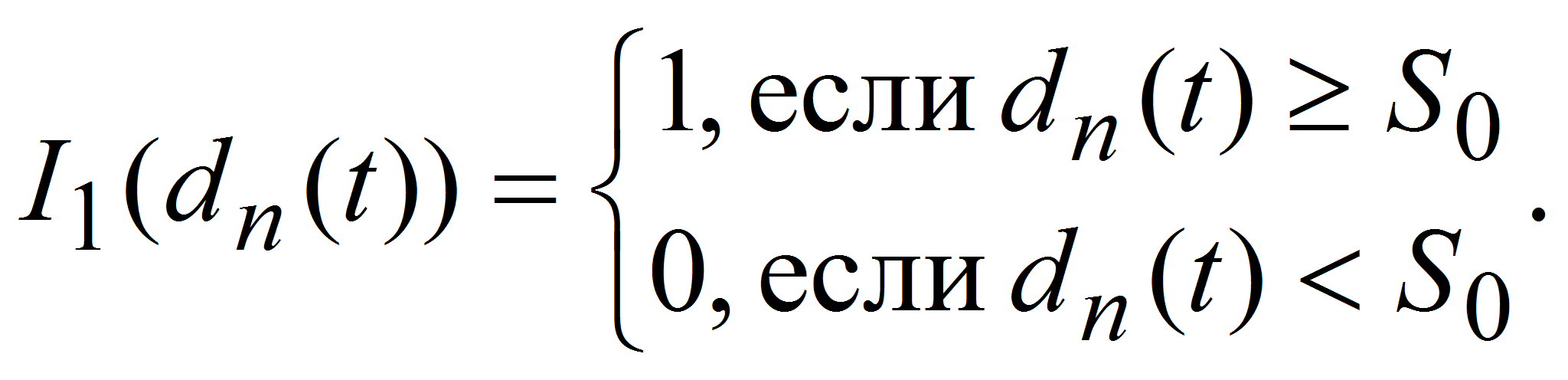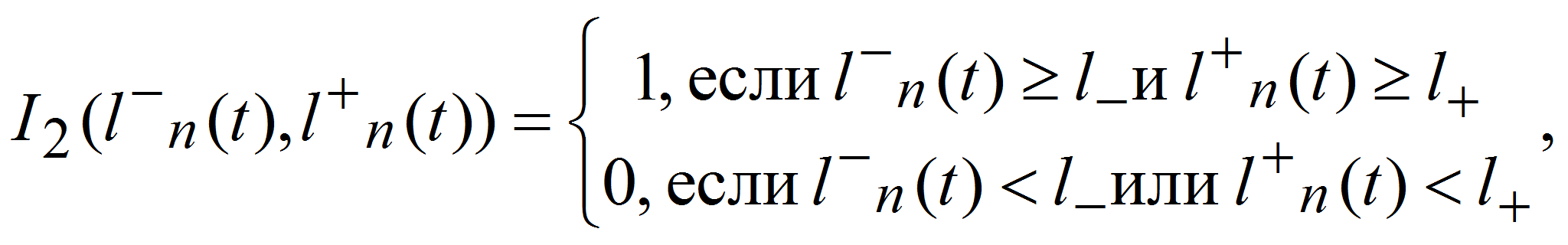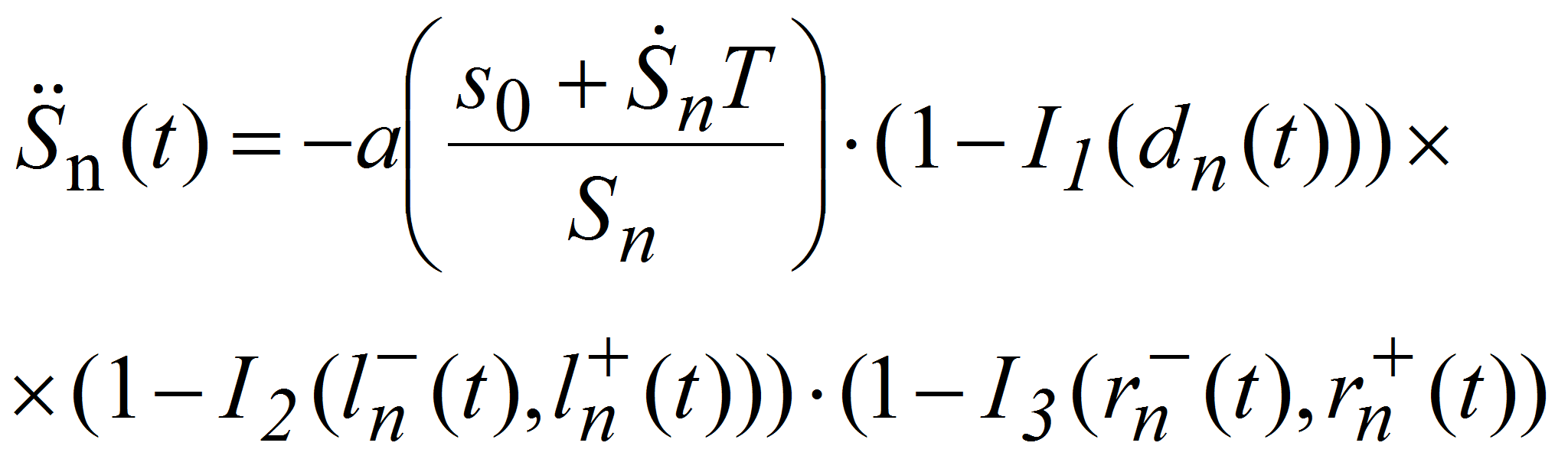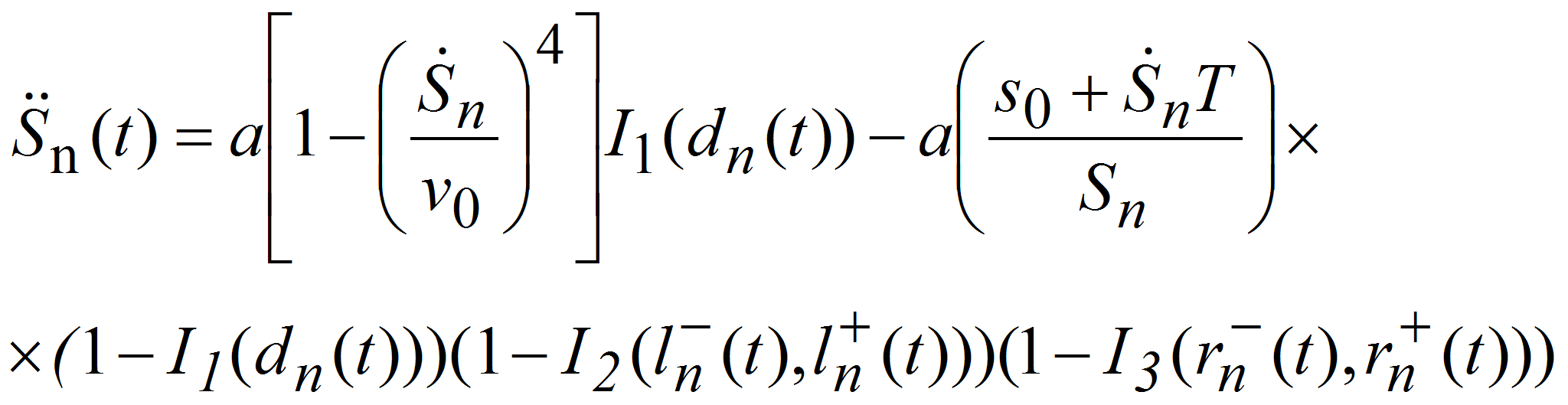При имитационном моделировании движения автотранспорта каждый исследователь выбирает свой уровень детализации и упрощения. Предлагаемая модель занимает промежуточный уровень между дискретными моделями клеточных автоматов, в которых движения отдельный автомобилей описываются упрощенно в потактовом режиме [], и микроскопическими моделями, детально описывающими движение отдельного автомобиля []. Упрощение описания движения отдельных автомобилей допустимо только до уровня, позволяющего решать основную задачу исследования.
Целью исследований является выбор оптимального цикла работы светофора, поэтому имитационная модель должна адекватно отражать закономерности движения потока автомобилей, проезжающего через регулируемый перекресток. С другой стороны, излишняя детализация динамики отдельного автомобиля приводит к существенному усложнению модели, введению значительного числа дополнительных параметров, невозможности существенного ускорения вычислений для получения статистических оценок.
Для достижения целей исследований выбрана гибридная математическая модель, в которой динамика разгона и торможения описывается непрерывными дифференциальными уравнениями, а смена полосы движения – упрощенно за один такт движения. Выбор шага дискретизации в такой модели является отдельной задачей, так как непрерывная и дискретная составляющая движения преобразуются по-разному.
Полученная имитационная модель верифицирована [], и использовалась для выбора оптимальной продолжительности цикла [].
- Постановка задачи
Рассмотрим движение отдельного автомобиля. Введем следующие обозначения:
n – индивидуальный номер автомобиля, n = 1,…,N;
j – номер полосы движения, j = 1,…, J;
Sn(t) – расстояние от начала отчета (считается вдоль полосы) для n-го автомобиля в момент t.
Будем обозначать jn(t) номер полосы, по которой движется n-ый автомобиль в момент t. В модели в каждый момент времени t положение автомобиля на дороге определяется двумя координатами: S и j. Расстояние S(t) является непрерывной функцией, которая изменяется в соответствии с дифференциальными уравнениями движения. Номер полосы j принимает целые значения, и смена полосы происходит скачком, таким образом, движение автомобиля описывается гибридной системой.
На рис. 1 изображен автомобиль n по отношению к другим автомобилям.
Рис. 1. Положение автомобиля n
по отношению
к другим автомобилям
При описании динамики разгона и торможения и условий смены полосы будем использовать упрощенный вариант модели умного водителя [], предложенный в [].
Найдем уравнения для вычисления параметром модели движения для каждого автомобиля (см. рис. 1).
1) Расстояние до впереди идущего автомобиля (по той же полосе):
(1)
2) Расстояние до впереди идущего автомобиля по левой полосе jn(t)+1:
(2)
3) Расстояние до позади идущего автомобиля по левой полосе jn(t)+1:
(3)
4) Расстояние до впереди идущего автомобиля по правой полосе jn(t) – 1:
(4)
5) Расстояние до позади идущего автомобиля по правой полосе jn(t) – 1:
. (5)
Каждая из перечисленных функций зависит от номера полосы движения автомобиля jn(t), расстояния от начала координат Sn(t), момента времени t и номера автомобиля n.
Описание модели отдельного автомобиля
Модель движения отдельного автомобиля состоит из 3-х компонент.
Модель ускорения автомобиля, в том числе движение без ускорения, как частный случай (условие I1): расстояние до ближайшего впереди идущего транспортного средства не менее заданного значения S0.
Условие перестроения автомобиля в левый ряд j+1 при условиях, что расстояние до ближайшего впереди идущего транспортного средства меньше заданного значения S0 (условие I1 не выполнено), и перестроение в левый ряд возможно (условие I2).
Условие перестроения автомобиля в правый j–1 ряд при условиях, что расстояние до ближайшего впереди транспортного средства меньше заданного значения S0 (условие I1 не выполнено), и перестроение в левый ряд невозможно (условие I2 не выполнено), но возможно перестроение в правый ряд (условие I3 выполнено).
Торможение автомобиля задается с помощью обыкновенного дифференциального уравнения, производится при нарушении условий I1, I2, I3.
Запишем условие движения автомобиля с ускорением a, и обозначим индикатор выполнения этого условия через I1(dn(t)):
(6)
Аналогично сформулируем условия возможности перестроения автомобиля в левую (I2)
(7)
- и правую (I3 ) полосы движения:
(8)
Таким образом, ускорение автомобиля происходит в случае, когда выполнено условие (6).
Запишем уравнение ускорения с условием (6):
-
(9)
где
– максимальное ускорение, м/с2,
–
текущая скорость автомобиля n, м/с,
– максимально-допустимая
скорость движения, м/с.
Запишем условия смены полос с учетом индикаторов выполнения условий. В момент t+δ, δ > 0, номер полосы j не меняется, если I1 = 1; номер полосы увеличивается на единицу j+1, если I1 = 0 и I2 = 1; и номер полосы уменьшается на единицу j – 1, если I1 = 0, I2 = 0 и I3 = 1:
(10)
В случае если I1 = 0, I2 = 0 и I3 = 0 происходит торможение и динамика описывается уравнением торможения, которое происходит только, в том случае если не выполняются условия I1, I2, I3, т.е. соответствующие индикаторы равны 0:
, (11)
где
– максимальное ускорение, м/с2;
– текущая скорость, м/с;
- Получили, что изменение расстояния от начала координат описывается уравнением:
. (12)
А условие смены полосы – соотношениями (10). В эти уравнения
входят функции
,
которые зависят от расположения остальных автомобилей на полосах
движения (см. рис. 1).
Таким образом, уравнения (10), (12) с условиями (6)-(8) описывают движение отдельного автомобиля с учетом расположения ближайших к нему машин.
- Вывод
В статье предложено описание движения отдельного автомобиля в потоке с использованием гибридных систем. Полученная модель легла в основу «Программы микромоделирования потоков автотранспорта на перекрестке» [].
Разработанная программа позволяет задавать входные параметры (габариты перекрестка, число полос движения, интенсивности движения автомобилей) и получать все необходимые выходные параметры (длина очереди, пропускная способность и т.д.). Также в программе можно задать параметры оптимизации, после чего программа выполнит отбор значений, соответствующих заданным параметрам. Все результаты можно скопировать в MS Excel, где построить необходимые графики, провести дальнейший анализ и выбрать оптимальный цикл светофора.
- Литература:
Sven Maerivoet, Bart De Moor Cellular automata models of road traffic // Physics Reports, Volume 419, Issue 1, 2005, Pages 1-64
Kesting A., Treiber M., Helbing D. Agents for Traffic Simulation // Multi-Agent Systems: Simulation and Applications, Chapter 11, Pages 325-356, 2008
Ахмадинуров М.М., Тимофеева Г.А. Верификация программы микромоделирования потоков автотранспорта // Вестник Московского автомобильно-дорожного государственного технического университета (МАДИ), 2011, №1(24). – С. 7–12. ISSN 2079-1364
Ахмадинуров М.М. Оптимизация светофорного регулирования с помощью программы моделирования транспортных потоков / М.М. Ахмадинуров. // Вестник ЮУрГУ. Серия «Компьютерные технологии, управление, радиоэлектроника». – 2010. – Вып. 12, №22(198). – С. 26–30. ISSN 1991-976X
Свидетельство об официальной регистрации программы для ЭВМ Ахмадинурова Максима Минихатовича «Программа микромоделирования потоков автотранспорта на перекрестке» № 2010616284 от 22.09.2010 г. / Зарегистрировано Федеральной службой по интеллектуальной собственности, патентам и товарным знакам
