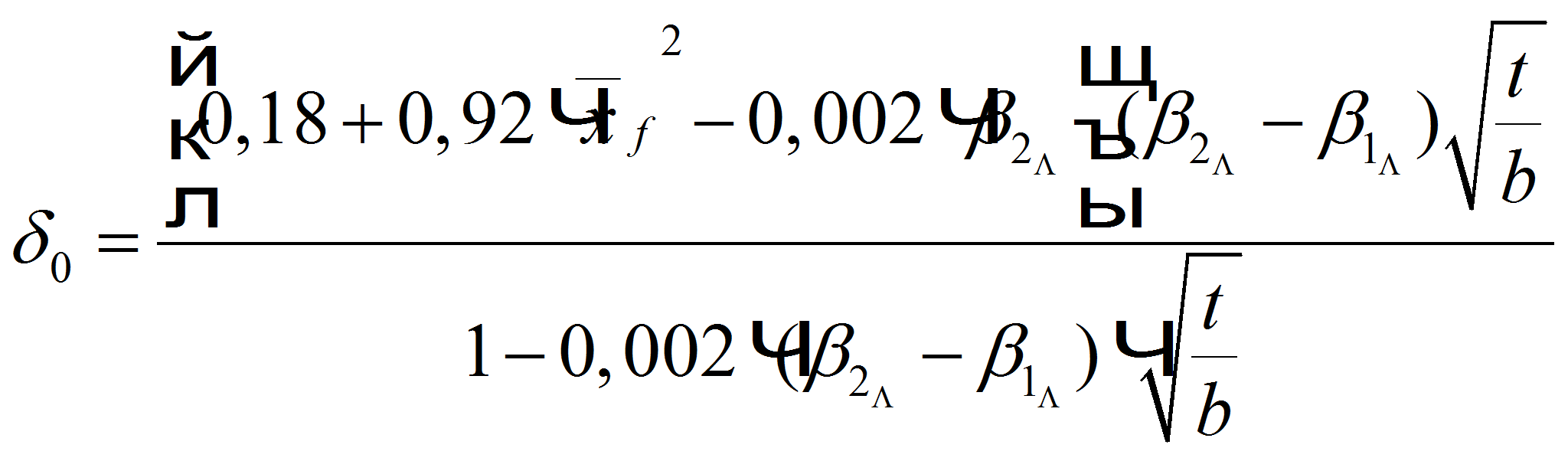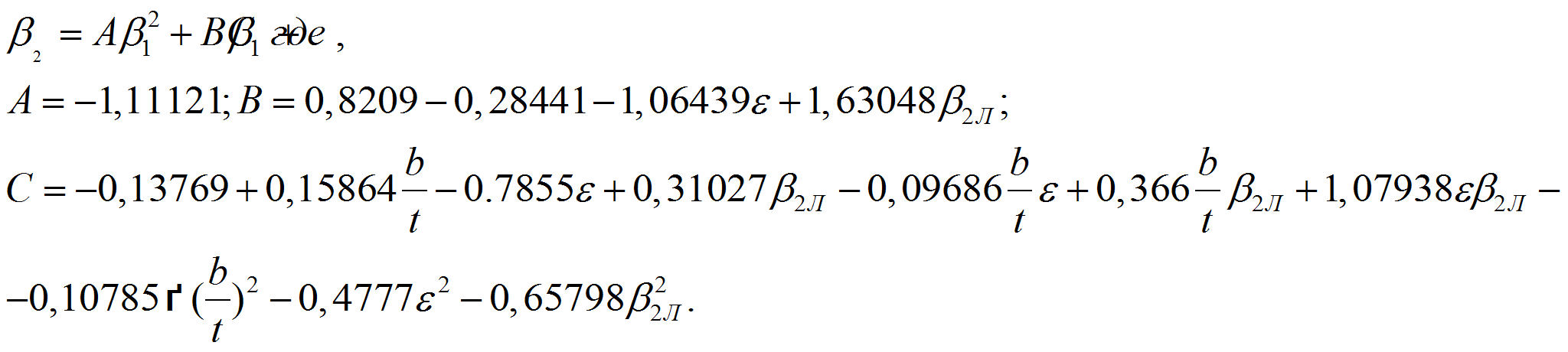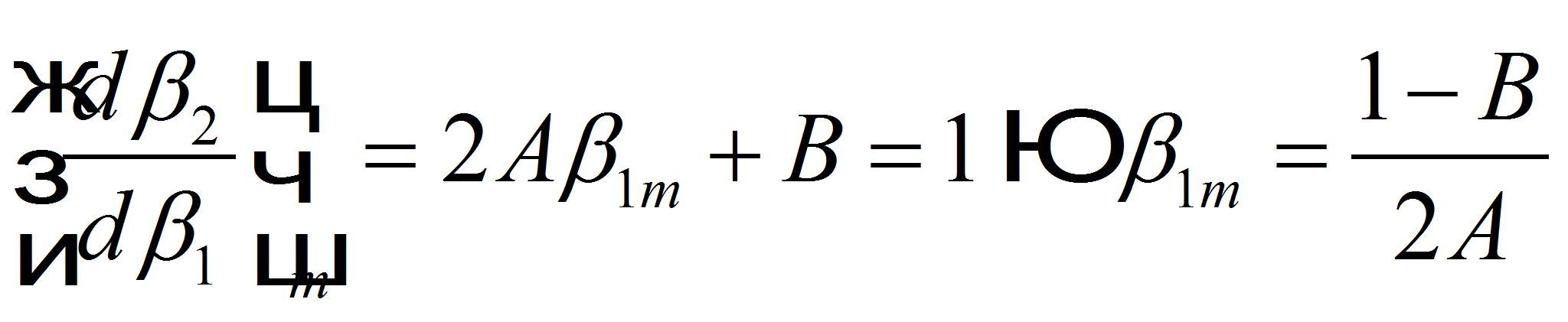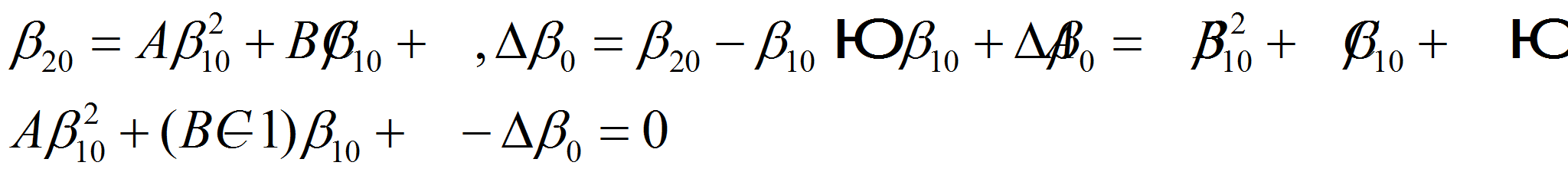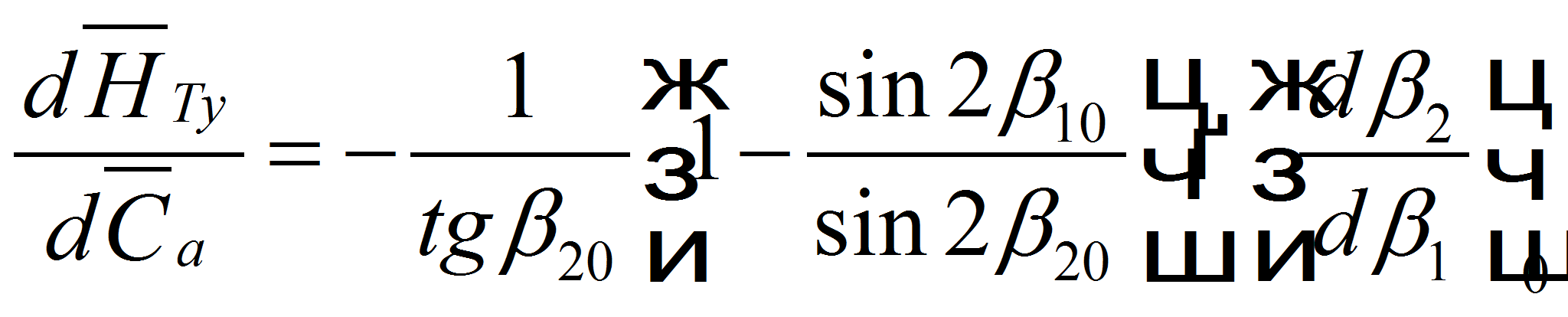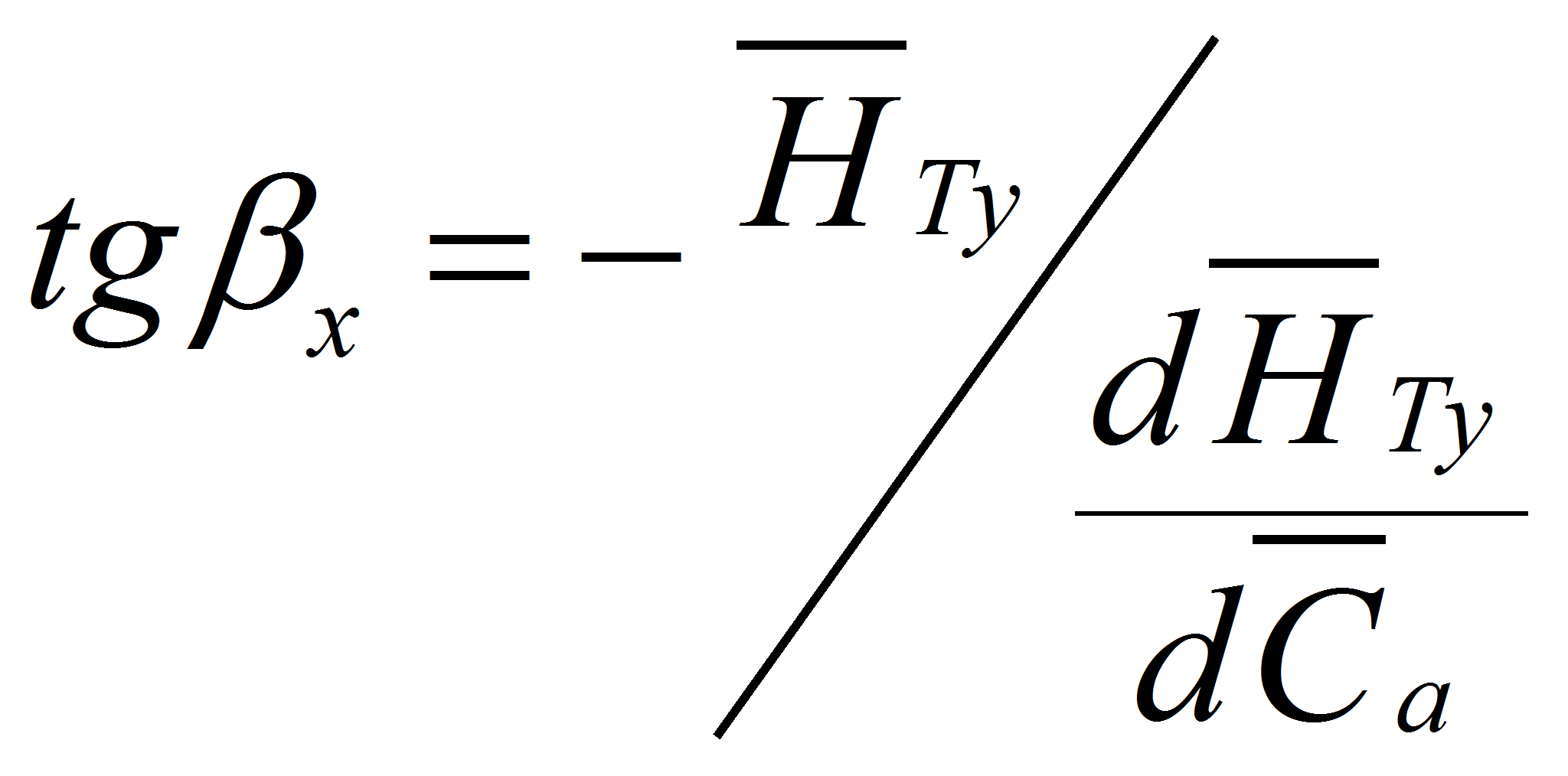При проектировании компрессоров размеры проточной части, число ступеней и их параметры определяются в результате газодинамического расчета. При этом обычно расчет ведется только для одного режима, который называется расчетным. Для определения параметров компрессора на других режимах используются характеристики компрессоров, полученные экспериментально. Поскольку на ранних этапах проектирования экспериментальные характеристики отсутствуют, проектировщик принимает решения в условиях неопределенности. В данной статье приводятся результаты анализа известных методов расчета характеристик решеток профилей, на основе которых, уже на этапе проектирования компрессора можно будет получать характеристики венцов, ступеней и многоступенчатых компрессоров для обоснованного выбора их конструкторских и режимных параметров.
При планировании физических или численных экспериментов по получению характеристик компрессоров, при оптимизации геометрии элементов проточной части (ПЧ) на этапе проектирования, при экстраполяции характеристик компрессоров (для моделирования запуска, анализа помпажа, авторотации), для образмеривания и унификации характеристик (что важно при идентификации моделей ГТД, при задании зависимости характеристик компрессоров от положения ВНА и НА, от степени эрозии и загрязнения ПЧ) наряду с новыми методами 3D САD-/CAE- моделирования сохраняется потребность в 2D - моделях. Поэтому изучение закономерностей протекания, развитие методов расчета характеристик решеток профилей остаются актуальными.
Авторами предлагается новый алгоритм и модель элементарных решеток, при этом осевые зазоры рассматриваются как элементарные решетки с густотой b/t→0. На первом этапе проанализированы известные модели и методы расчета [1,2,4,5]. Обнаружено что в ряде случаев эти модели плохо согласуются с экспериментальными данными, недостаточно точны.
Обобщенные данные по
плоским решеткам строятся на основе влияния величин b/t, β2
(или β1)
на ∆β. Прежде чем привести такие обобщенные данные по
результатам испытаний решеток при малых скоростях набегающего потока,
отметим, что выбор режима работы решетки вблизи
![]() не представляется возможным не только потому, что при этом к. п. д.
ступени падает, но и в связи с тем, что при возникновении срывного
режима возникает неустойчивость течения в компрессоре, когда
эксплуатация компрессора невозможна или сильно затруднена. Поэтому
режим работы решетки и все обобщения строят для некоторого
номинального угла поворота потока
не представляется возможным не только потому, что при этом к. п. д.
ступени падает, но и в связи с тем, что при возникновении срывного
режима возникает неустойчивость течения в компрессоре, когда
эксплуатация компрессора невозможна или сильно затруднена. Поэтому
режим работы решетки и все обобщения строят для некоторого
номинального угла поворота потока
![]() для решеток РК и
для решеток РК и
![]() для решеток НА, обеспечивая необходимый запас относительно срывных
режимов. Предложена следующая методика: предлагается брать за
расчетный режим именно номинальный, который отличается от
оптимального, т.е. расчетный режим отдельных ступеней смещен по
отношению к режиму с максимальным КПД и находится в области с более
низким КПД, но с более высоким запасом устойчивости.
для решеток НА, обеспечивая необходимый запас относительно срывных
режимов. Предложена следующая методика: предлагается брать за
расчетный режим именно номинальный, который отличается от
оптимального, т.е. расчетный режим отдельных ступеней смещен по
отношению к режиму с максимальным КПД и находится в области с более
низким КПД, но с более высоким запасом устойчивости.
Рассмотрим несколько вариантов нахождения номинального режима, которую в дальнейшем можно использовать для нахождения характеристики решетки профилей в целом:
Вариант 1. В работе [8] авторами предложена регрессионная зависимость угла выхода из решетки от угла набегания и геометрических параметров решетки, полученная при использовании результатов продувок решеток профилей при небольших скоростях потока:
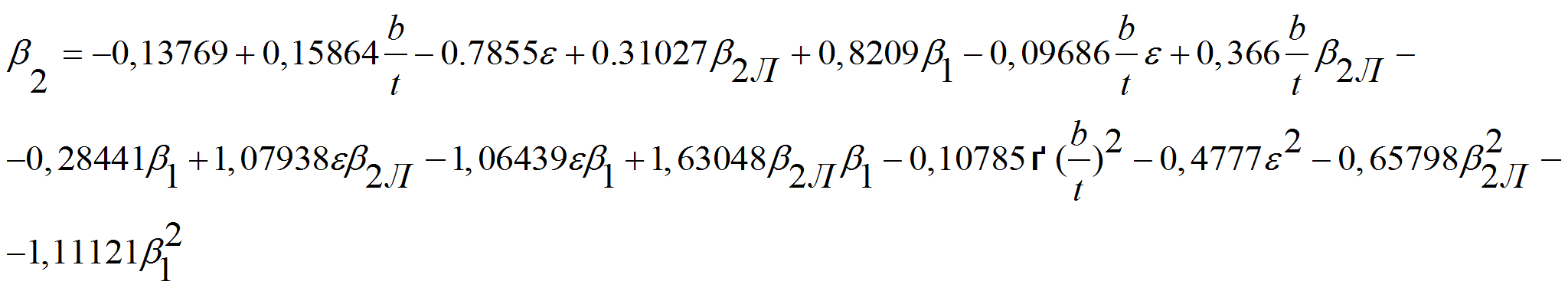 Выполненный
авторами анализ показал, что эта зависимость в целом плохо
согласуется с вышеприведенными результатами, с результатами продувок
решеток ([3,7]) и с теоретическими представлениями. По существу ее
можно использовать лишь вблизи номинального режима.
Выполненный
авторами анализ показал, что эта зависимость в целом плохо
согласуется с вышеприведенными результатами, с результатами продувок
решеток ([3,7]) и с теоретическими представлениями. По существу ее
можно использовать лишь вблизи номинального режима.
Вариант
2. Для
определения номинального (по Хауэллу) угла отставания![]() авторами, после проведенного анализа ряда источников, предлагается
использовать, например, зависимость из [5], где предлагается
определять угол отставания на номинальном режиме по формуле
авторами, после проведенного анализа ряда источников, предлагается
использовать, например, зависимость из [5], где предлагается
определять угол отставания на номинальном режиме по формуле
![]() ,
где
,
где
![]() [1]
и
[1]
и
![]() [1].
При сравнении с экспериментальными продувками решеток профилей было
установлено, что зависимость [3] является более точной, чем другие, и
при сравнении с экспериментальными продувками дает погрешность не
более 10-20.
Поэтому при получении формулы для номинального угла отставания
предлагается использовать эту зависимость, которая преобразована
авторами к виду:
[1].
При сравнении с экспериментальными продувками решеток профилей было
установлено, что зависимость [3] является более точной, чем другие, и
при сравнении с экспериментальными продувками дает погрешность не
более 10-20.
Поэтому при получении формулы для номинального угла отставания
предлагается использовать эту зависимость, которая преобразована
авторами к виду:

Для
определения номинального угла поворота потока Δβо
используется зависимость
![]() приведенная
в [5], где
приведенная
в [5], где
![]() .
Данная зависимость пригодная для решеток профилей с густотой b/t=1,
для решеток профилей с другой густотой используется поправочный
коэффициент
.
Данная зависимость пригодная для решеток профилей с густотой b/t=1,
для решеток профилей с другой густотой используется поправочный
коэффициент
![]() , где
, где
Вариант 3. Для большей точности авторами предлагается комбинация первого и второго способа, при этом номинальный угол отставания определяется по формуле:
Далее предложен метод для нахождения точки, близкой к номинальной (например, по критерию Хауэлла), определять в ней производную dβ2Л/dβ1Л и далее использовать выведенные авторами формулы. Для этого регрессионная зависимость из [8.] авторами преобразована к виду:
Такое представление удобно для определения максимального и номинального режимов.
Для определения максимального режима находим:
По
универсальному графику Хауэлла [2] определяем (в данном случае
«квазиноминальный» режим, поскольку исходный максимум
регрессионной формулы Казанджана под сомнением)
![]() ,β1о=
β1m -0,4Δ βо
,β1о=
β1m -0,4Δ βо
Таким образом были получены точки максимального и «квазиноминального» режимов.
В этой «квазиноминальной» точке определяется производная и по вышеприведенным формулам отыскиваются производная для коэффициента теоретического напора и базовая линия его протекания в зависимости от коэффициента расхода (точнее от тангенса угла набегания).
Далее с учетом этого по вышеприведенным формулам определяем параметры базовой линии коэффициента теоретического напора:
Дальнейшие
построения (аналогично методу Ольштейна Л.Е.) по предложенному
авторами алгоритму [6] связаны с учетом потерь и определением в
номинальной точке коэффициента изоэнтропического напора, построение
линий с учетом поправок (на скорость набегания и т.д.), построение
линий КПД, переход в традиционные координаты
![]() и т.д.
и т.д.
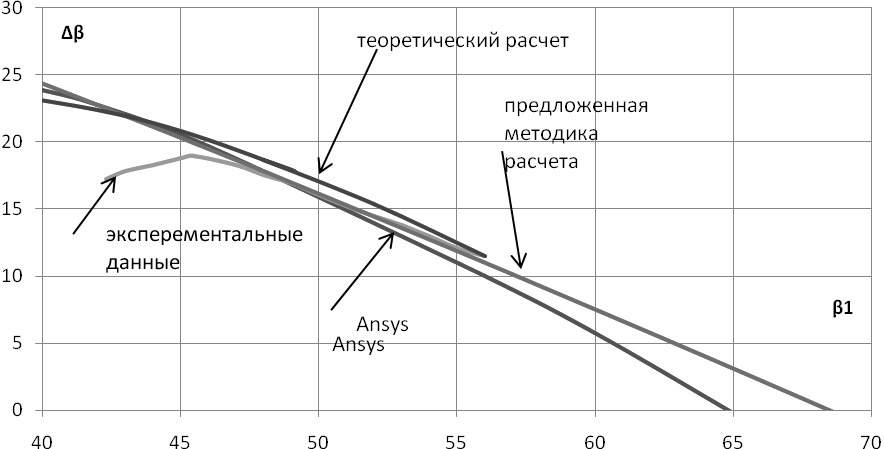
Для проверки полученной
методики было произведено сравнение результатов расчета базовой линии
коэффициента теоретического напора конкретной решетки с параметрами
b/t=1,
![]() ,
,![]() (рис. 1) с экспериментальные данными [3] и с данными, полученными по
известной методике расчета Казанчана П.П. [8] и с результатами 3D
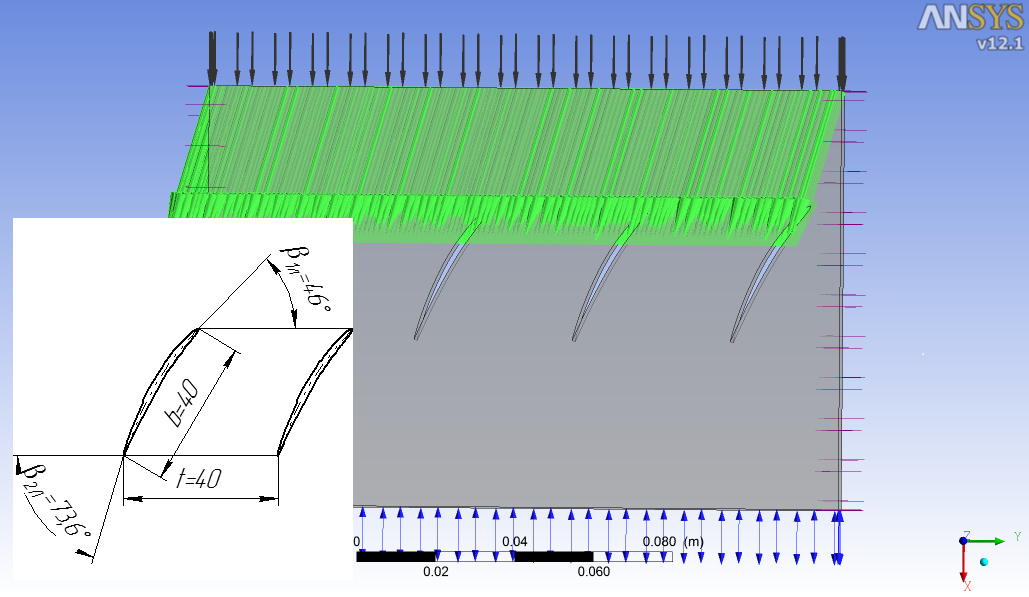
CAD/CAE-моделирования в системе Ansys CFX. Для этого сформирована 3D
CAD- модель данной решетки. 3D CAE-модель с граничными условиями,
параметрами исследуемой решетки профилей и фрагментом течения на
входе в решетку представлена на рис. 2.
(рис. 1) с экспериментальные данными [3] и с данными, полученными по
известной методике расчета Казанчана П.П. [8] и с результатами 3D
CAD/CAE-моделирования в системе Ansys CFX. Для этого сформирована 3D
CAD- модель данной решетки. 3D CAE-модель с граничными условиями,
параметрами исследуемой решетки профилей и фрагментом течения на
входе в решетку представлена на рис. 2.
Рис. 1
Рис. 2 3D CAD-/CAE- модель с граничными условиями,
и геометрические характеристики решетки профилей
- Заключение
Полученные результаты позволяют планировать эксперимент по продувке решеток профилей, анализировать и редактировать результаты экспериментов. Предложенная методика позволяет использовать её для расчета характеристик лопаточных венцов, ступеней, многоступенчатых осевых компрессоров. Получение характеристики компрессора является одной из ключевых задач на различных стадиях проектирования от эскизного до технического проекта. Достоверная характеристика компрессора (каскада компрессора) позволяет рассчитать характеристики разрабатываемого изделия на установившихся (дроссельная, климатическая, высотно-скоростные характеристики) и на неустановившихся режимах (динамическая характеристика ГТД) с высокой точностью. При проектировании компрессора предложенная методика позволяет производить выбор геометрических параметров лопаточных венцов, а в эксплуатации – производить учет влияния на характеристики изменения геометрии лопаток (за счет эрозии, загрязнения и т.д.). Дальнейшее развитие данного метода для получения характеристик с учетом потерь будет освещено в последующих статьях.
Работа выполнена при финансовой поддержке РФФИ (№10-08-00795)
- Литература:
- Холщевников К. В. Теория и расчет авиационных лопаточных машин: Учеб. для авиац. вузов и фак-ов. – М.: Машиностроение, 1970. – 610 с.
- Ольштейн Л. Е., Процеров В. Г. Метод расчета осевого компрессора по данным продувок плоских решеток// Труды ЦИАМ №150. – М: Издательство «Бюро Новой Техники», 1948. – 64 с
- А.И.Бунимович, Г.С.Орлова Сборник аэродинамических характеристик плоских компрессорных решеток. Выпуск 1. - М: ЦИАМ 1955 - 70c.
- Бунимович А.И., Святогоров А.А. Исследование влияния геометрической формы исходного профиля на аэродинамические характеристики плоской компрессорной решетки МАП, Труды N231, 1952
- Белоусов А.Н., Мусаткин Н.Ф.. Радько В.М. Теория и расчет авиационных лопаточных машин. - Самара: Государственный аэрокосмический университет , 2003. - 344 с.
- Кривошеев И.А., Рожков К.Е. Анализ рабочих процессов и характеристики лопаточных машин. // Вестник УГАТУ. Т. 14, № 5(40), 2010. С. 3-10
Emery J.C., Herring J.I.,Erwin J.R. 'Systematic two- dimensional cascade test of NACA-65 serias compressor blades at low speeds', NACA RML51G,31, 1951.
-
Казанчан П.П., Караваев
Б.В., Серков В.И., Шишкин В.Н.
Обобщение результатов продувок плоских компрессорных решеток методом регрессионного анализа/ЦИАМ .-М.:ЦИАМ,1975 .-64 с.-Труды/ЦИАМ;№679