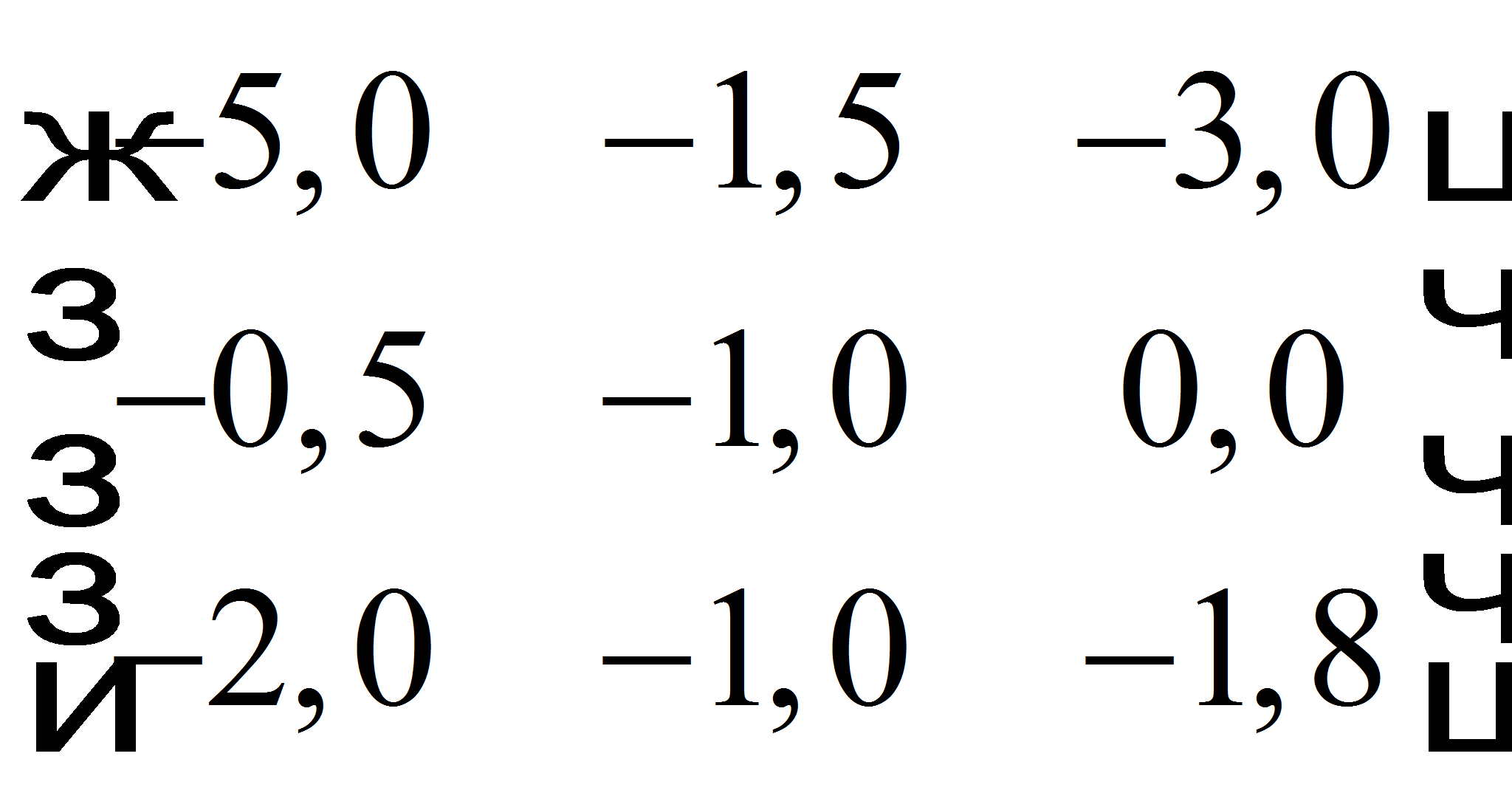Рассматривается вопрос о выборе оптимальной стратегии в конфликтной ситуации. С помощью теории игр для двух бескоалиционных противников определяются стратегии, которые приведут если не к положительному выигрышу, то, по крайней мере, к наименьшим потерям. Теоретические аспекты рассматриваются на примере планирования виртуальной боевой операции. Описывается математическая модель принятия решений в условиях конфликта противоборствующих сторон.
Информация является одним из наиболее значимых в настоящее время факторов, способствующих развитию коалиционных отношений между государствами. В настоящее время все также справедливо высказывание «Кто владеет информацией, тот владеет миром». Кроме того, на первый план выходит необходимость эффективно использовать имеющуюся информацию. Теория игр и теория оптимального управления позволяют принимать правильные решения в различных конфликтных и предконфликтных ситуациях. Наиболее часто при выборе одного варианта действия из многих возникают ситуации, в которых участвуют несколько противоборствующих сторон, например, группа захвата и задерживаемый противник. Такие ситуации называются конфликтом. В условиях конфликта принимающему решение необходимо учитывать не только свои собственные интересы, но и цели и интересы противника, которые в общем случае неизвестны. Таким образом, возникает достаточно непростая ситуация выбора оптимального действия для каждого из участников конфликтной ситуации.
Благодаря наличию общих закономерностей в развитии самых разных систем возможно исследование их математическими методами. Данные математические модели строятся с помощью такого раздела математики, как исследование операций (теория игр является частью этого раздела). Исследование операций (ИО) как математический инструментарий, поддерживающий процесс принятия решений в самых разных областях человеческой деятельности, описывает всевозможные средства, позволяющие обеспечить лицо, принимающее решение, необходимой количественной информацией, полученной научными методами. Исследование операций сформировалось на стыке математики и разнообразных социально-экономических дисциплин.
Первым в области математического моделирования сложных военно-стратегических задач был Фредерик Ланчестер. Одним из наиболее важных результатов, полученных им, стало открытие в 1916 г. так называемого квадратичного закона, количественно связывающего достижение победы с такими основными факторами, как численное превосходство силы и эффективность оружия. Было показано, что при одновременном вступлении в бой численное превосходство в живой силе более важно, чем применение более совершенного вооружения, поскольку главную роль играет сосредоточение собственных войск и расчленение сил противника. Примером использования квадратичного закона Ланчестера являлась тактика Нельсона в сражении при Трафальгаре.
Математические модели принятия решений в условиях конфликта, рассматриваемые в так называемой теории игр, могут найти широкое применение в военно-тактических разработках планов операций. Первые работы по теории игр были сделаны Цермело и Борелем в начале XX века. Большой вклад в современной теории игр внес великий ученый нашего времени Джон фон Нейман. Он сформулировал основные идеи и результаты и доказал основную теорему теории игр. С этого времени теория игр стала развиваться более интенсивно. Появление и быстрое развитие ЭВМ обеспечивает возможность эффективного решения громоздких конфликтных игровых задач. Несмотря на значительные достижения, в теории игр остается еще немало проблем. Основными направлениями, активно разрабатываемыми в данной области, являются:
- выработка решения определенных игр;
- доказательство теорем существования решений;
- разработка методов нахождения решений;
- практические аспекты использования.
На основе построенной математической модели выбираются методы ее аналитического решения и способы реализации в виртуальной и реальной действительности (см. рис. 1).
Рис. 1. Построение математической модели
Под игрой понимается математическая модель конфликта, в котором принимают участие две или более стороны, стремящиеся к достижению разных целей. Участники игры с общими стратегическими интересами могут объединяться в группы или коалиции. Чаще всего в игровых моделях присутствуют два игрока – противоборствующие стороны. Участниками игры могут стать также два преступника, которые в ходе следствия имеют противоположные интересы – возложить ответственность за содеянное на другого. Выбор стратегии в конфликтной ситуации означает план действий игрока при различных возможных действиях противника. Очевидно, что стратегии могут быть более или менее удачными. Мерой эффективности действий игрока является так называемый выигрыш. Выразить результат различных исходов количественно весьма затруднительно. Но в данном случае это необходимо, т.к. в теории игр рассматриваются только такие игры, в которых выигрыш выражается числовыми данными: стоимость, расстояние, очки, баллы и т.д. Очевидно, исход игры, а следовательно, выигрыш каждого игрока зависит от применяемых ими стратегий. Если же в реальной ситуации возникает случай, когда исход для участника полностью зависит от него самого, то такая ситуация не рассматривается как игровая. Проигрыш рассматривается как отрицательный выигрыш. Поэтому в дальнейшем рассматриваются только выигрыши.
При представлении
конфликтной ситуации в военном деле возникает ряд трудностей в связи
с описанием правил, условий, игроков, стратегий, ходов и выигрышей,
т.е. в описании математической модели предстоящих военных действий по
сценарию «если-то». Задача заключается в том, чтобы
данную конфликтную ситуацию по возможности привести к формализованной
игре без значительных потерь реальных целей, найти метод решения
такой модели, провести расчеты и анализ. Рассмотрим наиболее важный
класс игры – бескоалиционную, в которой игроки-противники не
могут вступать в коалиции или договариваться о некоторых соглашениях.
Важным случаем бескоалиционной игры является ситуация, в которой
количество игроков равно двум, а выигрыш одного равен проигрышу
другого. Такие игры называются антагонистическими или играми двух лиц
с нулевой суммой. Действительно, если выигрыш первого игрока
обозначить через
,
то выигрыш второго будет равен
,
и общая сумма выигрышей равна
Первый игрок делает определенный выбор из нескольких возможных
ситуаций (для простоты двух, трех), не зная о решении второго. А
второй, не будучи информированным о выборе первого, принимает свое
решение. Необходимо установить стратегию, которая приведет если не к
положительному выигрышу, то, по крайней мере, к наименьшим потерям.
Рассмотрим для примера
виртуальную игру в чистых стратегиях, приближенную к практическим
военным действиям. В ходе проведения боевой операции возникла
следующая ситуация. Противник продвигается с запада на восток по
одному из трех возможных направлений
.
Группе захвата поставлена боевая задача: выти наперерез противнику,
навязать им открытый бой и одержать победу над ним. Группа захвата
имеет также три маршрута движения
.
Пересечение путей движения обеих групп определяет место проведения
боя. Таким образом, существует 9 возможных участков столкновения. Все
они располагаются на разных относительных высотах, приведенных на
рис.2.
Рис. 2. Высоты предполагаемой стратегической операции
Группе захвата выгоднее навязать открытый бой противнику на местности с наименьшей относительной высотой. Противник чувствует себя более уверенно и безопасно в горах. Участки предполагаемого боя имеют разные высоты, указанные в таблице. Необходимо определить, какой маршрут движения группы захвата оптимален. В качестве выигрыша для группы захвата в каждом случае реализации выбора места схватки рассмотрим высоту данной местности, взятую с обратным знаком, так как увеличение высоты стратегически не выгодно для нее и, следовательно, выигрыш меньше. Матрица полученных выигрышей имеет вид:
.
(1)
Для нахождения оптимальной стратегии группы захвата воспользуемся следующим методом. Для каждого варианта решения найдем наиболее неблагоприятный исход в зависимости от действий противника, затем из полученных значений выигрышей выберем максимальный. Таким образом будет получен гарантированный лучший выигрыш при всевозможных худших действий противника, т.е. находится по принципу «лучший из худших». Для этого анализируются все строки матрицы, соответствующие разным маршрутам группы захвата. При выборе первого маршрута (А) наихудший выигрыш равен -5,0; маршрута (B) - из второй строки наименьшим является число -1,0; маршрута (C) - наименьшее значение из третьей строки матрицы -2,0. Максимальным из найденных значений выигрышей является -1,0. Таким образом, при выборе второго маршрута (B) бой произойдет на участке не выше 1,0 км. Эта высота обеспечивается при выборе противником 2-го пути. При выборе других направлений противником высота места предполагаемого боя еще ниже – 0,5 км и 0 км. Следовательно, второй маршрут (B) для группы захвата является оптимальным в смысле наименьших потерь. Так называемая цена игры для группы захвата равна -1,0.
Рассмотрим теперь действия противника в данной конфликтной ситуации и найдем их оптимальную стратегию поведения. Естественно, они стремятся как можно к большим значениям высоты, чтобы укрыться в труднодоступной местности. Поэтому исходим из противоположного алгоритма. Найдем максимальные значения в столбцах, а затем выберем минимальное из них. Это и будет тот выигрыш группы захвата, добиться больше которого противник не позволит. Максимальные элементы столбцов: -0,5; -1,0; 0,0, а минимальный из них равен -1,0. Таким образом, на 2-м маршруте противник не допустит выигрыша группы захвата больше, чем -1,0 и относительная высота боя будет не ниже 1,0 км. Цена игры для противника равна -1,0. Следовательно, цена игры для обоих противников одинаковая и конфликт разрешим в чистых стратегиях. Получили так называемую седловую точку. Если посмотреть на рельеф местности сбоку, то можно увидеть, что на пересечении маршрутов (B) и (2) находится седловина.
Матричные игры в чистых стратегиях определенной размерности можно автоматизировать, например, в табличном процессоре MS EXCEL. При этом используются встроенные функции: МАКС, МИН, ЕСЛИ.
-
- Литература:
Петросян Л.А., Зенкевич Н.А., Семина Е.А. Теория игр. М.: Высш.шк., 1998. 304 с.
Вентцель Е.С. Элементы теории игр. М.: Наука, 2008. 360 с.
Покорная О.Ю. О выборе оптимальных стратегий в планировании боевых операций. Всероссийской научно-практическая конференц. «Инновации в авиационных комплексах и системах военного назначения». Воронеж, ВАИУ, Ч.10, 2009, с.194-198.
