Реконструкция – процесс восстановления трехмерной поверхности из двумерной поверхности. Двумерная проекция – это плоское изображение (фотография) какого-либо объекта или поверхности, не содержащее в себе никакой явной информации о глубине сцены.
Человеческий глаз в состоянии оценить глубину сцены на плоском изображении по некоторым косвенным признакам:
Затенение – распределение света позволяет оценить наклон поверхности.
Текстура – искажение текстуры также позволяет оценить наклон поверхности.
Фокус – ограничиваетглубину сцены по резкости.
Движение – при движении разные точки сцены двигаются на разные расстояния.
Другие признаки – форма, симметрия, цвета и др.
На сегодняшний день созданы алгоритмы, которые используют некоторые косвенные признаки, для реконструкции объектов.
Формы из затенения.
Если взять изображение гладкого, затененного объекта (рисунок 1), то его форму можно оценить очень легко, при помощи отражения и затенения.
Рисунок 1 – Гладкий объект
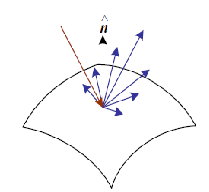
Нормаль к поверхности объекта плавно изменяется, изменение яркости отражения можно представить функцией угла между локальной ориентацией поверхности и источником света (рисунок 2).
Рисунок 2 – Отражение света
Проблема восстановления формы из поверхности с переменной интенсивностью отражения, известная как форма из затенения, имеет множество решений и алгоритмов. Большинство из них строится на том факте, что рассматриваемая поверхность имеет равномерное альбедо и отражение, направление источников света либо известны, либо могут быть откалиброваны с помощью эталонного объекта.
Форма из текстуры
Искажение ракурса, наблюдаемое вобычных текстурах, также позволяет получить полезную информацию о локальной ориентации поверхности. Такие алгоритмы обычно состоят из нескольких шагов: нахождение повторяющегося шаблона или измерении локальных частот для вычисления местных аффинных трансформаций, и на каждом последующем этапе определение локальной ориентации поверхности (рисунок 3, рисунок 4).
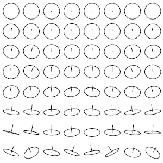
Рисунок 3 – Текстура с повторяющимся шаблоном
Рисунок 4 – Вычисленные локальные нормали
Форма из фокуса.
Глубина объекта определяется степенью размытости, которая увеличивается при увеличении расстоянии между поверхностями объекта и линзой камеры. Существует множество алгоритмов для оценки глубины, в зависимости от расфокусировки. Для реализации этих алгоритмов, необходимо решить несколько практических вопросов:
Размытие (расфокусировка) увеличивается в обоих направлениях при движении фокусной плоскости. Необходимо использовать два или более изображения, полученных с разным фокусным расстоянием.
Размеры объекта могут изменяться при изменении фокуса или перемещении объекта.
Степень расфокусировки должна быть надежно оценена. Для этого лучше всего использовать различные рациональные фильтры (общие модели для фильтрации включают в себя как свертку (числитель Z-преобразования), так и обратную фильтрацию (знаменатель Z-преобразования)):
Получение формы из фокуса, в общем случае, возможно только с помощью специального устройства (рисунок 5).
Рисунок 5 – Датчик диапазона фокусировки
Форма из движения.
Рассмотренные выше методы позволяют реконструировать только некоторые типы объектов, обладающих строго определенными физическими свойствами. Так, например, для корректной реконструкции формы из затенения, поверхность исходного объекта должна обладать ламбертовым отражением. Для восстановления формы из текстуры, текстура объекта должна обладать хорошо выраженным и выделяемым шаблоном. Получение формы из фокуса сопряжено с трудностями технического характера – датчик диапазона фокусировки может себе позволить приобрести не каждая видеолаборатория.
В основу метода формы из движения положен принцип извлечения информации о трехмерной сцене за счет движения (объекта или камеры). Используя векторы оптического потока и так называемые точки интереса, можно вычислить поверхности, углы, а также траекторию движения камеры (датчика). В основном реализованы алгоритмы, выполняющие реконструкцию в контролируемой лабораторной среде.
Предлагаемый алгоритм позволит выполнить реконструкцию для некалиброванных изображений, полученных произвольной камерой. Калибровка позволяет заранее задавать позицию камеры в пространстве, а также вычислять внутренние и внешние параметры самой камеры, позволяющие вычислить гомографию. Реконструкция формы из некалиброванных изображений – более сложная задача: необходимо из последовательности изображений получить не только перемещение камеры, но и форму поверхности.
Для калиброванных изображений известны следующие матрицы:
K – матрица внутренней калибровки камеры,
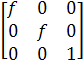 ,
где f–фокусное
расстояние.
,
где f–фокусное
расстояние.C –матрица внешней калибровки камеры,
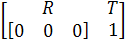 ,
где R–
вектор вращения, T–переноса.
,
где R–
вектор вращения, T–переноса.E – существенная(essential) матрица,
 ,
в ней закодировано перемещение камеры (или камер в случае
стерео-реконструкции).
,
в ней закодировано перемещение камеры (или камер в случае
стерео-реконструкции).
Общий алгоритм получение формы из движения следующий:
Вычислить на каждом изображении «особые точки».
Вычислить матрицы калибровки.
Сопоставить изображения, используя особые точки.
Используя эпиполярные ограничения, с помощью триангуляции построить карту глубины.
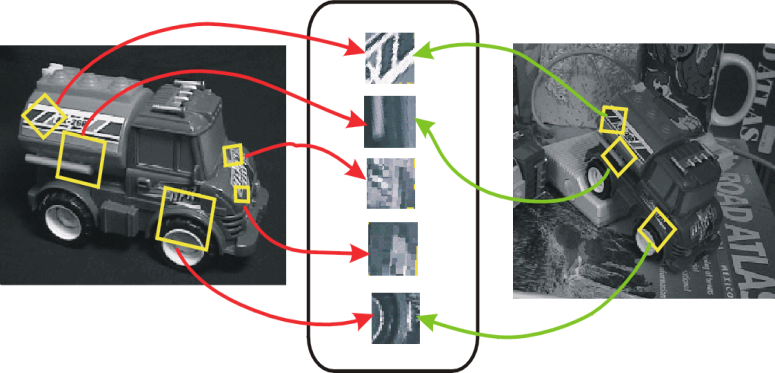
Оптический поток – оценка движения между двумя близкими кадрами. Обычно применяется ко всем пикселам кадра. Для некалиброванных изображений оптический поток целесообразно вычислить только для некоторых особых точек. Особая точка – такая точка, которую легко выделить на обоих изображениях, которая так же инвариантна к повороту, перемещению, масштабированию и изменению освещения. В качестве таких точек обычно выбирают углы в определенной локальной области. Каждой области присваивают уникальный дескриптор, инвариантный к различным геометрическим и цветовым преобразованиям (рисунок 6).
Рисунок 6 – Выбор особенностей
В случае использования
некалиброванных изображений, матрицы K,
C,
E
вычислить не удастся. Матрица E
содержит всю информацию о геометрии камер и используется для
вычисления эпиполярных линий. Вместо матрицы E
можно вычислить фундаментальную матрицу F
=
![]() .
Матрица F
подобна матрице E
за исключением того, что F
оперирует пиксельными координатами изображения, а E
оперирует физическими координатами. Матрица F
имеет ранг 2 и 7 параметров, 2 на каждое эпиполе и 3 на гомографию
двух изображений. Использование
матрицы F
называют слабой калибровкой. Матрицу F
можно вычислить различными способами, но чаще всего используют
алгоритм RANSAC
(RANdomSAmpleConsensus).
.
Матрица F
подобна матрице E
за исключением того, что F
оперирует пиксельными координатами изображения, а E
оперирует физическими координатами. Матрица F
имеет ранг 2 и 7 параметров, 2 на каждое эпиполе и 3 на гомографию
двух изображений. Использование
матрицы F
называют слабой калибровкой. Матрицу F
можно вычислить различными способами, но чаще всего используют
алгоритм RANSAC
(RANdomSAmpleConsensus).
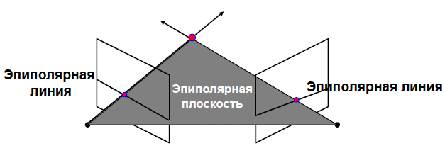
С помощью матрицы F можно вычислить эпиполярные ограничения – эпиполярные линии. Эпиполярные линии ограничивают размерность поиска соответствий между особыми точками на изображениях (рисунок 7).
Рисунок 7 – Эпиполярная геометрия
Особые точки обоих изображений должны лежать на соответствующих эпиполярных линиях. Теперь используя эффект триангуляции можем построить карту глубины. Эффект триангуляции – точка сцены находится как пересечение двух лучей – луч проходит через оптический центр и точку изображения.
Данный метод позволяет провести реконструкцию объекта из набора некалиброванных фотографий, используя только вектор оптического потока и эффект триангуляции. Метод реализован на языке С++ с помощью свободной библиотеки OpenCV.
Литература:
Fischler, M. A. and Bolles, R. C. (1981). Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Communications of the ACM, 24(6), 381–395.
Richard Szeliski, Computer Vision: Algorithms and Applications, 957, 2010
Л. Шапиро, Дж. Стокман, Компьютерное зрение, 752, 2006
Антон Конушин, Ольга Баринова, Вадим Конушин, Антон Якубенко, Александр Велижев, Стерео-реконструкция, МГУ, Graphics&MediaLab, 2008.
Gary Bradski and Adrian Kaehler, Learning OpenCV, 555, 2008