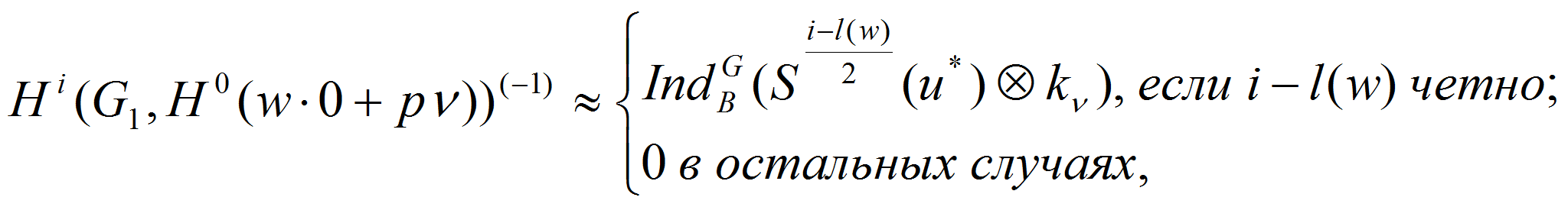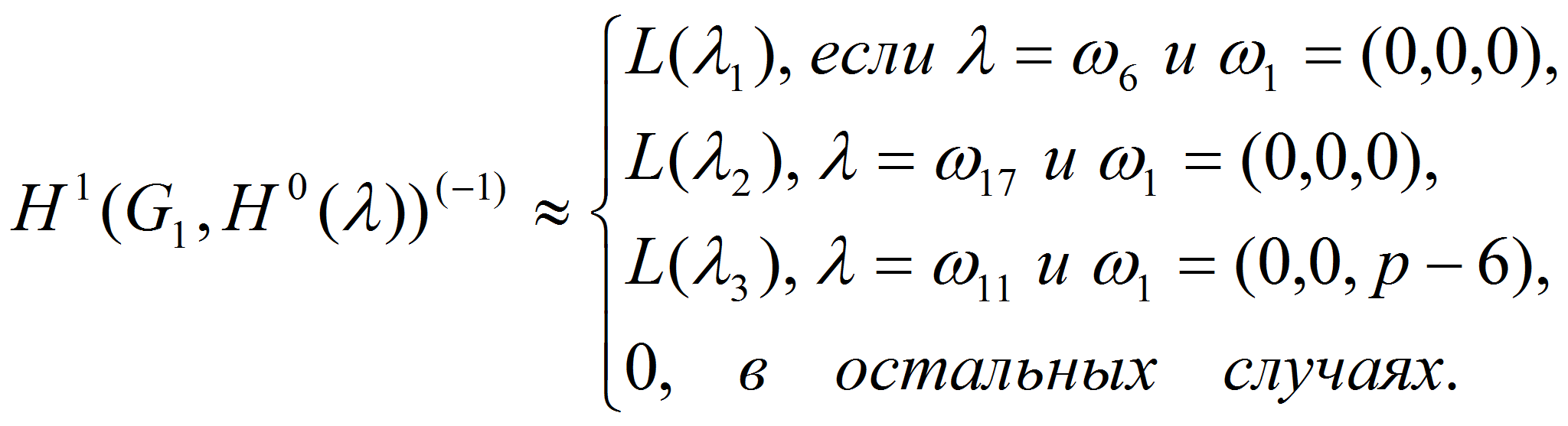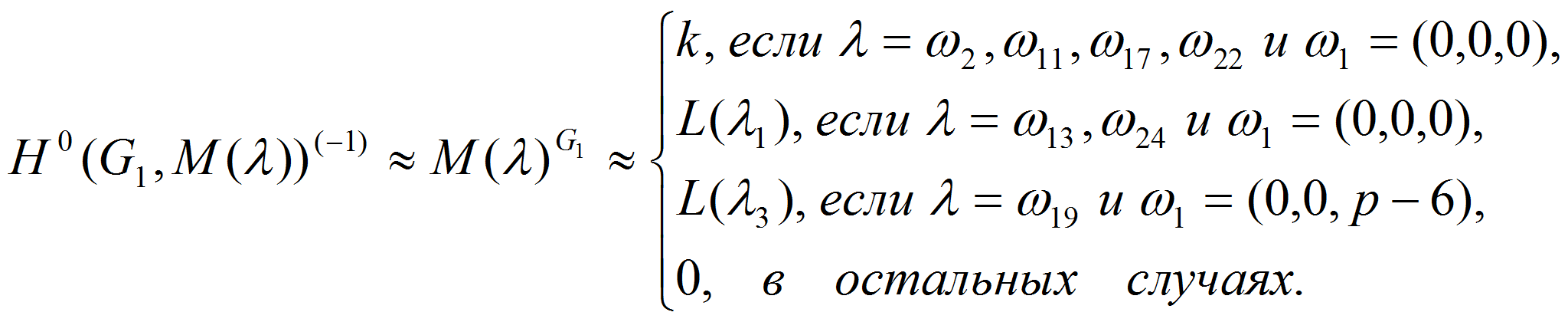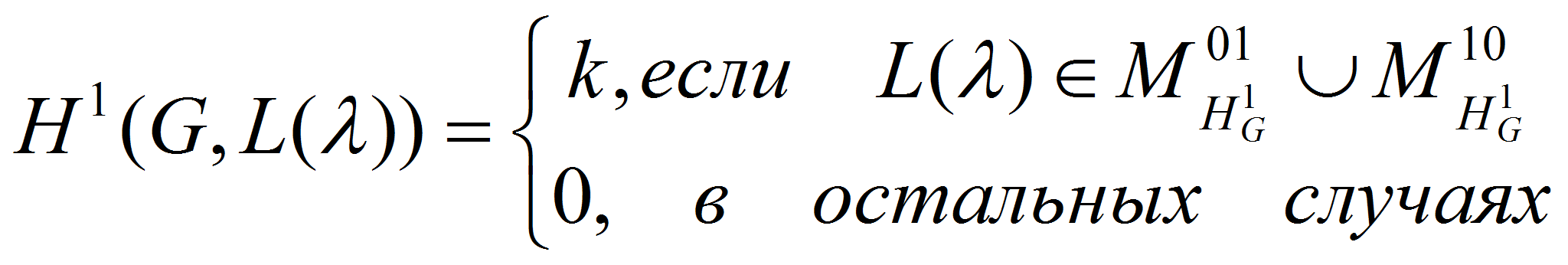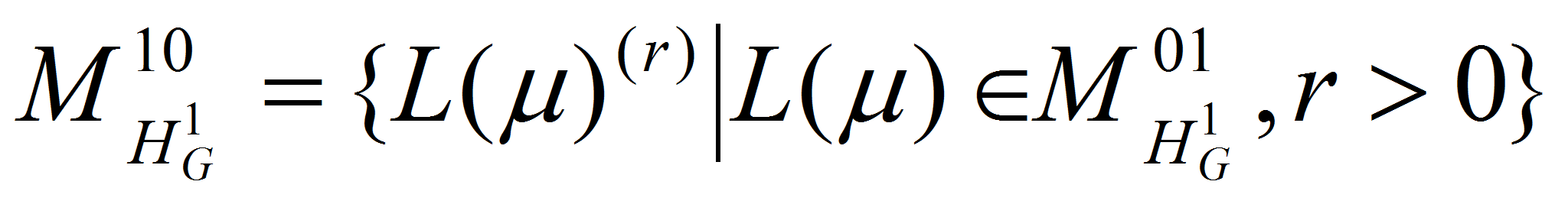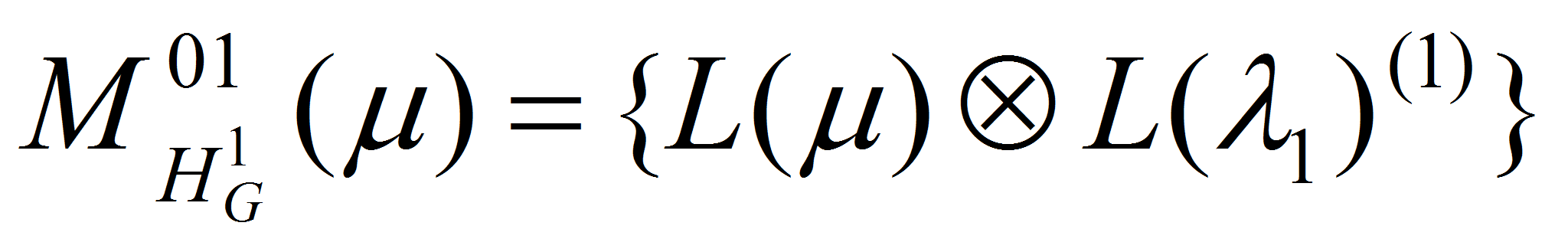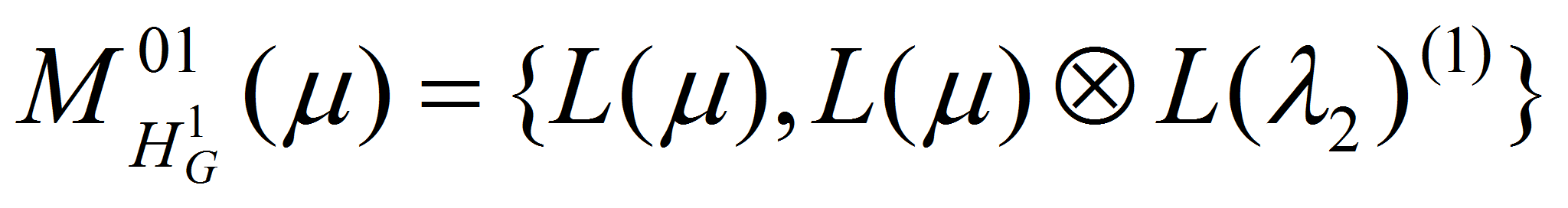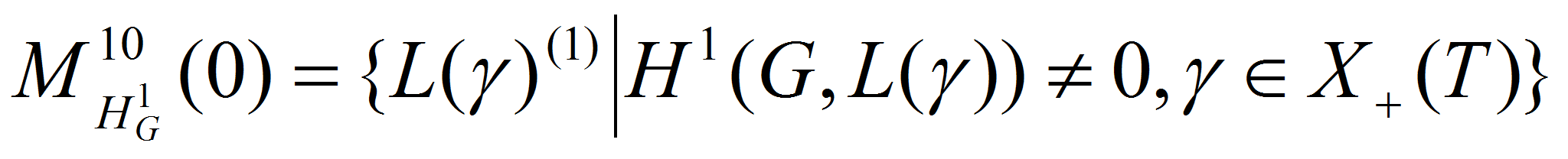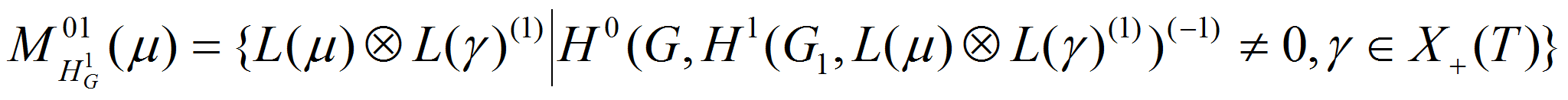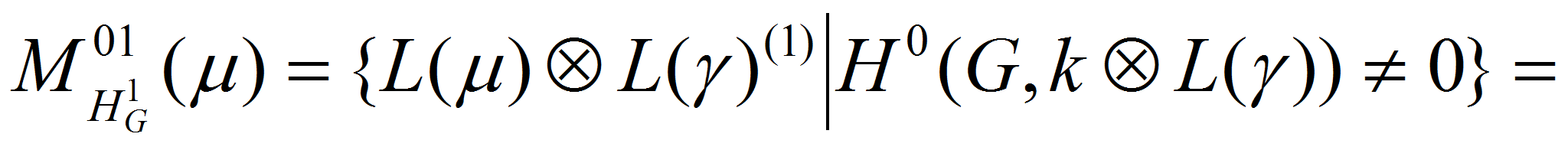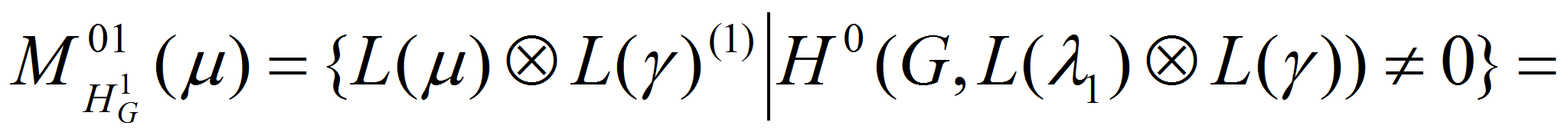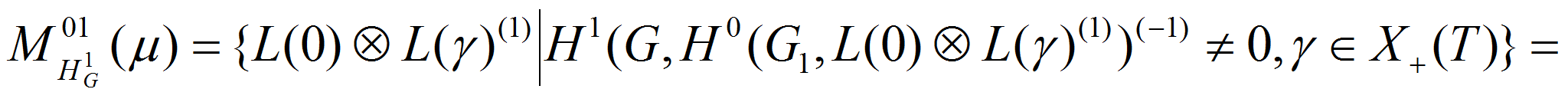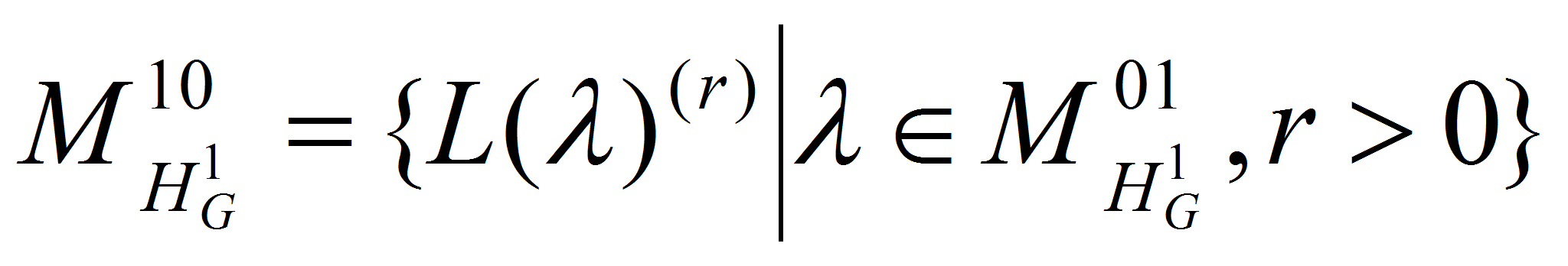Когомологии первой степени простых модулей над алгебраической группой типа в положительной характеристике

Дано полное описание когомологий первой степени простой алгебраической группы типа над алгебраически замкнутым полем характеристики с коэффици­ентами в простых модулях.

Пусть G – полупростая односвязная алгебраическая группа над алгебраичес­ки замкнутым полем характеристики , G₁ – ядро отображения Фробениуса F : G → G. Обозначим через В и Т соответственно подгруппу Бореля и максимальный тор группы G. Будем считать, что унипотентный радикал В соответствует отрицательным корням системы корней R группы G.

Пусть для всех – множество доминантных весов и для всех – множество ограниченных весов, где Х(Т) – группа характера максимального тора Т, а S – множество простых корней.

Когомологии первой степени простых модулей полностью вычислены только для следующих односвязных алгебраических групп: [1], [2], [3]. Для когомологий второй степени аналогичные результаты получены для [1], [4], [5], [6]. Для простых модулей, размерности которых не превосходят р, вторые когомологии вычислены для всех алгебраических групп [7].

Пусть L – рациональный G-модуль. Через L^(d) обозначим кручение Фробениуса степени d для L. Тогда существует единственный и рациональный G-модуль V такой, что V^(d) = L. Обозначим его через L^(-d).

Когомологии над индуцированных модулей для вычислены в [8]:

(1)

где – максимальная нильпотентная подалгебра алгебры Ли группы , соответствующая отрицательным корням, – симметрическая алгебра на , – длина элемента .

Пусть теперь – полупростая односвязная алгебраическая группа типа и . Обозначим через фундаментальные веса и будем использовать сокращенную запись для . Так как из фундаментальных весов является наименьшим только , то имеются ровно альковы аффинной группы Вейля с ограниченными весами. Обозначим их через . Пусть , , , , , , – элементы аффинной группы Вейля . Тогда ; ; ; ; ; ; ; , , где – нижний фундаментальный альков аффинной группы Вейля.

Кроме того, существует следующие двадцать альковов с неограниченными весами: , , , , , , , , , , , , , , , , , , , .

Предложение 1. Пусть , и – ограниченный неприводимый -модуль. Тогда , кроме следующих случаев:

(i) , если и ;

(ii) , если и ;

(iii) , если и ;

(iv) , если и .

Доказательство. По принципу связанности только следующие 48 ограниченных весов -связаны с нулевым весом:

.

Согласно (1) только 3 модуля имеют нетривиальную когомологию , причем

Пусть . Только 7 модулей имеют нетривиальное инвариантное подпространство , причем

Согласно [9, c.298, 301],

. (2)

Тогда только для перечисленных выше 9 простых ограниченных модулей первые группы когомологий нетривиальны. Кроме того, используя (2), получаем изоморфизмы -модулей (i) – (iv). Предложение 1 доказано.

Для простого G-модуля L(λ) спектральная последовательность Линдона-Хохшильда-Серра имеет вид [10], 1.6.6.(3):

. (3)

Если - ее стабилизированное значение, то

(4)

Определим множество простых модулей . Из (1) и теоремы Стейнберга о тензорном произведений следует, что

(5)

Теорема 2. Пусть – односвязная алгебраическая группа типа над алгебраически замкнутым полем характеристики и – конечномерный простой G-модулъ. Введем на рассмотрение множества весов

= , если ,

= , если ,

и предположим, что . Тогда

где и .

Сначала докажем следующие вспомогательные утверждения.

Лемма 3. Пусть . Тогда

(i) , если ;

(ii) , если ;

(iii) , если ;

(iv) , если ;

(v) .

Доказательство. (i) Пусть . По (3)

.

Далее, по предложению 1(iv) и по лемме 1.1 работы [11],

.

(ii) Пусть . По (3)

.

Далее, по предложению 1(ii) и по лемме 1.1 работы [11],

.

(iii) и (iv) доказываются аналогично предыдущему случаю.

(v) Если μ = 0, то по (3),

. Доказательство леммы завершено.

Лемма 4. Пусть . Тогда

(i) ;

(ii) .

Доказательство. (i) следует из (3) и предложения 1. Утверждение (ii) вытекает из леммы 3(v) и утверждения (i) данной леммы. Лемма доказана.

Предложение 5. Пусть и – конечномерный простой G-модулъ. Тогда

(i) ;

(ii) ;

(iii) .

Доказательство. По теореме Стейнберга о тензорном произведений λ можно пред­ставить в следующем виде: λ = μ + pγ, где и . По определению является когомологией последовательности . Тогда , если

, когда (6)

Для выполнение условия (6) очевидно. Докажем, что = 0 если ≠ 0. Если ≠ 0, то по предложению 1, . Тогда согласно (3), = 0.

Для любой спектральной последовательности и . Это доказывает справедливость утверждений (i) и (ii). Утверждение (iii) следует из утверждений (i), (ii) данной леммы и формулы (2). Предложение доказано.

Доказательство теоремы 2. Очевидно, что . Кроме того, согласно лемме 3 множества также попарно не пересекаются. Тогда утверждение теоремы следует из предложения 5 и леммы 4. Доказательство теоремы 2 завершено.

Литература:

1. Stewart D.I. The second cohomology of simple SL₂-modules // arXiv:0904.0623v2 [math.RT], 2009.

2. Yehia S. El. Extensions of simple modules for the universal Chevalley group and parabol­ic subgroup.- Warwick: Ph.D. Thesis. - 1982.

3. Ye Jiachen. Extensions of simple modules for the group Sp(4,K) // J. London Math. Soc. - 1990. - V. 2(41). - P. 51-62.

4. Stewart D.I. The second cohomology of simple SL₃-modules // arXiv:0907.4626vl [math.RT], 2009.

5. Ibraev S.S. The second cohomology groups of simple modules for Sp₄(k) // Intern. algebraic conf. dedicated to the 70^th birthday of A.V. Yakovlev. - St. Peterburg, Russia. - 2010. - P. 113-114.

6. Ибраев Ш.Ш. О второй когомологии простых модулей над 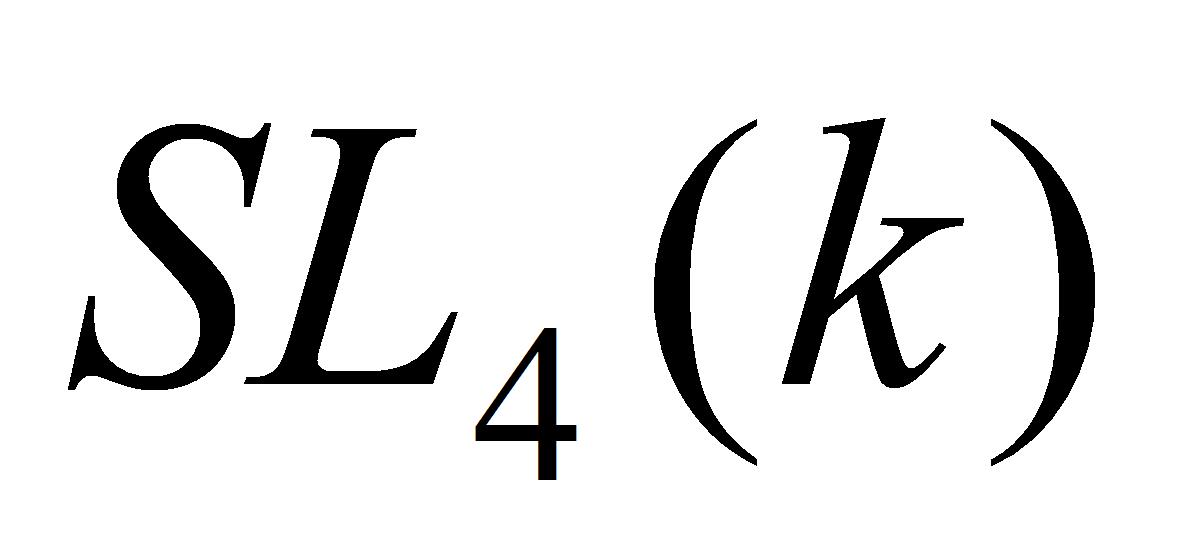в положительной характеристике // Материалы II межд. Научно-практ. Конф. «Наука в современном мире». - Москва.- 2010. С. 273-278.

7. McNinch G.J. The second cohomology of small irreducible modules for simple algebraic group // Pacific. J. Math. - 2002. - V. 204, No. 2. - P. 459-472.

8. Andersen H.H., Jantzen J.C. Cohomology of induced representations for algebraic groups // Math. Annalen. - 1984. - Vol. 269. - P. 487-525.

9. Jantzen J.C. First cohomology groups for classical Lie algebras // Progress in Math. - 1991. - Vol. 95. - P. 289 - 315.

10. Jantzen J.C. Representations of algebraic groups. Boston: Pure and Applied Mathe­matics. V. 131, 1987.

11. Sullivan J.B. Frobenius operations on Hochschild cohomology // Amer. J. Math. - 1980. - V. 102, No 4. - P. 765-780.

Работа выполнена при финансовой поддержке государственной программы фундаментальных исследований Ф. 0508 МОиН РК.