Управление финансами крупных экономических структур (корпораций, банкой и т.д.) предполагает создание многочисленных инвестиционных портфелей с целью диверсификации рисков, возникающих под влиянием различных непредсказуемых и не поддающихся детерминированному описанию факторов. При этом диверсификация рисков, как правило, включает в себя и решение оптимизационных задач, в которых целевой функцией является количественное измерение риска.
В предлагаемой работе рассматривается одна из подобных задач, характерной особенностью которой заключается в том, что количественная оценка риска портфеля исследуется и зависимости от выделенного для него объема капитала, а другие факторы, влияющие на риск, не учитываются.
The Decision of One Problem of Minimization Risk in Mnogoportfelnaya Models
Management of the finance of large economic structures (corporations, banks etc.) assumes creation of numerous investment portfolios for the purpose of a diversification of the risks arising under the influence of factors various unpredictable and not giving in to the determined description. Thus the diversification of risks, as a rule, includes also the decision of optimizing problems in which criterion function is quantitative measurement of risk.
In offered work one of the similar problems which prominent feature consists that the quantitative estimation of risk of a portfolio is investigated also dependences on the volume of the capital allocated for it, and other factors influencing risk is considered, aren't considered.
Ключевые слова: управление финансами, модель финансирования, минимизация риска.
Keywords: management of the finance, financing model, risk minimization
1. Предположим, что некоторая финансовая структура (например, корпорация) поставила перед собою цель формировать m инвестиционных портфелей из циркулирующих на финансовом рынке рисковых ценных бумаг.
Пусть по каким-то соображениям ценные бумаги разделены на n групп и каждый портфель может быть сформирован из ценных бумаг, входящих только в одну из этих групп.
Пусть, далее, на создание i-го портфеля из j-ой группы ценных бумаг выделено денежная сумма 
и формирование 
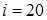портфеля из j-ой группы бумаг связан с портфельным риском, который выражается некоторой функцией 
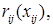зависящей только от выделенного капитала 
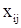. Относительно функций 
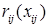будем считать, что они принимают неотрицательные, конечные значения в некоторой заданной области.
Назовём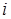 
-ый портфель, формирующийся из 
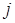-ой группы ценных бумаг, (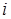,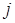) – портфели.
Таким образом, возможны много различных способов определения функций портфельных рисков, причем в рамках одной и той же модели эти функции могут быть представлены в различных формах для различных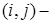 
портфелей.
Для описания совокупности, состоящей из m портфелей, введем матрицу S, элементы которой определяются следующим образом:
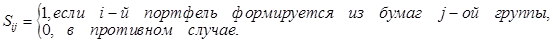
Эта матрица может быть названа матрицей назначений между портфелем и группами ценных бумаг, так как формирование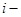 
го портфеля из бумаг 
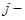ой группы можно рассматривать как назначение 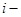го портфеля к 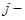ой группе (или наоборот).
Тогда условие, что каждый портфель составляется только из одной группы ценных бумаг, означает, что матрица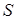 
содержит в каждой строке только одну единицу.
Обозначим через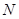 
множество всех матриц назначений, удовлетворяющих этому условию.
В самом общем случае количественная оценка совокупного риска всех вместе взятых портфелей может быть определена как функция, определённая на наборах:
При описанных условиях, финансовая структура, составляя m инвестиционных портфелей должна минимизировать свой совокупный риск,
а) нахождением матрицы назначения;
б) распределением имеющегося капитала между портфелями.
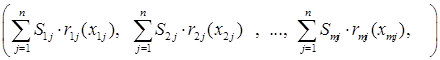
т.е.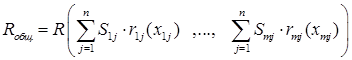 
Таким образом, требуется найти такую матрицу назначений и такое распределение наличного ограниченного капитала, при которых функция R достигает своего минимального значения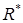 
:
(1)
где матрица S удовлетворяет условиям
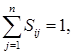для всех 
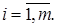(2)
Кроме того, поскольку величины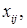 
фигурирующие в выражении функции 
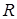, суть объёмы распределённых между портфелями инвестиций. Если объём капитала имеющегося у финансовой структуры равен K то при условии, что этот капитал полностью распределяется между m портфелями для величин 
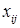должно выполняться следующие условия:
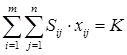(3)
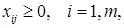
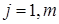(4)
В некоторых практических задачах к условиям задачи может быть добавлено условие целочисленности (или дискретности) переменных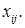 
Как видно из структуры задачи, она является двухпараметрической оптимизационной задачей, причём, по параметру S некоторым вариантам классической нелинейной задачи о назначениях, а по параметру 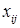нелинейной задачей оптимального распределения ресурсов.
Однако, попытки решения этих двух задач независимо друг от друга обречены на неудачу, потому что, чтобы решить задачу о назначениях, требуется знание оптимального распределения капитала и наоборот, чтобы решить задачу об оптимальном распределении ресурсов, нам должна быть известна матрица оптимального назначения. Следовательно, эта задача должна быть решаться таким образом, чтобы было возможным находить оптимальное назначение и оптимальное распределение одновременно.
2. О методе решения задачи.
В общем случае функция R может иметь сложную структуру, создающую в сочетании с двухпарацентричностью определенные вычислительные трудности. Однако анализ структуры задачи показывает, что для некоторых классов целевой функции данная задача может быть сведена к однопараметрической задаче оптимального распределения ресурсов. Одним из этих классов является класс функций, неубывающих по каждому аргументу на отрезок [0, к]. Для этого класса изложим вкратце суть процедуры вышеупомянутого преобразования.
Обозначим через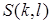 
матрицу из множества 
, в которой элемент 
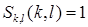, а остальные элементы зафиксированы и выделим из подмножество 
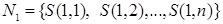. Элементы 
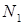отличаются друг от друга только первыми строками.
Рассмотрим задачу минимизации, развёрнутую по подмножеству :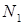
, 
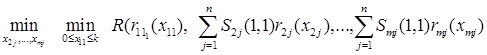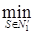
(5)
…………………………………………………………………………
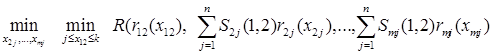
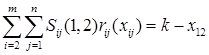
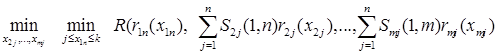
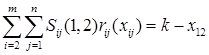
Здесь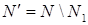 
. Отметим следующие особенности задачи (5)
а) Минимизация по переменным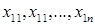 
проводится на одном и том же отрезке [0, к].
б) Из свойств элементов 
следует, что
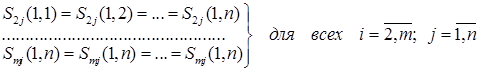
Из сказанного и из того, что 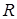неубывающая функция вытекает, что задача (5) эквивалентна следующей задаче:
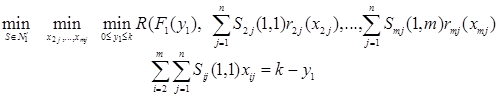
где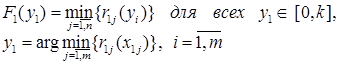 
Описанную процедуру будем называть агрегированием задачи (5) к задаче (6).
Далее, изменяя один единственный элемент в какой-нибудь
строке, отличной от первой вновь, выделяем подмножество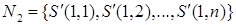 
и агрегируем по 
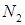, соответствующие задачи. Этот процесс продолжаем до тех пор, пока во всех агрегированных задачах первым аргументом функций 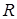не станет 
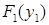. Этим завершается процесс агрегирования по первому аргументу функции .
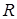Продолжая, таким образом, этот процесс для 2-го, 3-го и т.д. для m-го аргументов, в конце концов, получим следующую полностью агрегированную задачу.
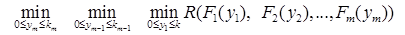(7)
или в эквивалентной форме
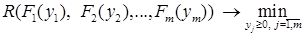(8)
При условиях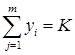 
(9)
(10)
где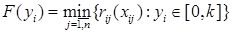 
(11)
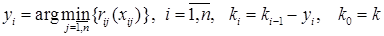(12)
Решение задачи (1, 4) можно начинать с определения функций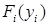 
по формуле (11). При этом используя (12) фиксировать значения переменных 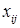в переменных 
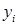. После того как определены переменные 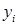функции 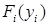можно перейти к решению задачи (8-10).
Сложность задачи (8-10) во многом зависит от степени нелинейности функции 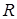. Для некоторых подклассов функции 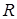решение задачи (8-10) существенно может упроститься.
Одним из таких подклассов является рекуррентно определенные функции.
Функция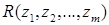 
называется рекуррентно определенной, если она удовлетворяет равенству:
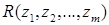
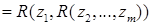
Хорошо известно, что оптимизационные задачи типа (8-10) легко решаются на основе принципа оптимальности Р.Беллмана [3].
В результате применения принципа оптимальности Р.Беллмана для решения задачи (8-10) получим следующие рекуррентное уравнение
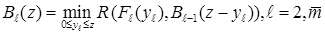(13)
При начальном уровне
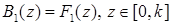(14)
В качестве примера укажем на следующие часто встречающиеся на практике подклассы функции .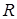
1) Если под совокупным риском всех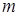 
портфелей понимается суммарный риск отдельных портфелей, тогда после преобразования функция 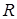и соответствующее рекуррентное уравнение (13) будут иметь вид:
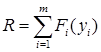
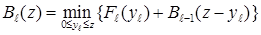
2) Если в качестве совокупного риска берётся максимальный риск из всех 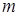портфелей, то имеем:
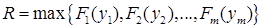
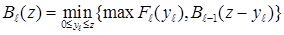
Аналогичный вид имеют и рекуррентные уравнения, в случае, когда совокупный риск принимается как минимальный риск всех 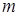портфелей. Относительно решения уравнений (13)-(14) отметим следующее: если в задаче (1)-(4) на переменные 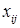налагается условие целочисленности, то тогда переменные 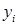также будут целочисленными и вычисление функций 
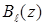будут производиться в целочисленных точках отрезка [0, z]. А если в задаче (1)-(4) условия целочисленности отсутствует, в уравнения (13)-(14) отрезок [0, z] дискретизируется известным способом.
Литература:
1. Малыхин В.И. Финансовая математика. М., 2000. 247 с.
2. Михалевич В.С., Кукса А.И. Задачи последовательной оптимизации в дискретных сетевых задачах оптимального распределения ресурсов. М.: Изд-во «Наука», 1983.
3. Беллман Р. Динамическое программирование. М.: Изд-во «Мир», 1960, 400 с.
