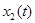Многочисленные модели процессов управления обучением описаны в литературе [2-5]. Для их качественного исследования может быть применен широкий спектр методов оптимального управления. В то же время задачи управления не всегда могут быть решены аналитически, что приводит к необходимости разработки численных методов их решения. В настоящее время разработано большое количество численных методов решения задач оптимального управления и нелинейного программирования и работа по их созданию и совершенствованию продолжается. Вычислительные подходы к решению задач нелинейного программирования и поиска оптимального управления получили широкое освещение и систематизацию в работах Ю.Г.Евтушенко [1]. Целью данной работы является разработка и исследование численного алгоритма для решения задачи управления обучением студенческого коллектива, формализуемой как задача оптимального управления.
Рассмотрим модель распределения времени между овладением знаниями и развитием умений. Полагаем, что знание состоит из информации (чистого знания) и умения (способности использовать имеющиеся сведения для достижения новых целей, методически работать). Пусть 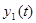 – объем сведений, накопленных студентом к моменту времени t (чистое знание),
– объем сведений, накопленных студентом к моменту времени t (чистое знание), 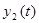 – объем накопленных умений, навыков решать задачи, разбираться в излагаемом материале;
– объем накопленных умений, навыков решать задачи, разбираться в излагаемом материале; 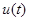 – доля времени, отведенного на накопление знаний в промежутке времени
– доля времени, отведенного на накопление знаний в промежутке времени 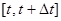 . Полагаем, что увеличение
. Полагаем, что увеличение 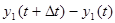 объема знаний студента пропорционально затраченному на это времени
объема знаний студента пропорционально затраченному на это времени 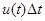 и накопленным умениям
и накопленным умениям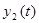 :
:
|
|
(1) |
где k1 > 0 – коэффициент, зависящий от индивидуальных особенностей учащегося.
Увеличение умений за то же время пропорционально затраченному на это времени 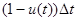 , имеющимся умениям
, имеющимся умениям 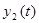 и знаниям
и знаниям 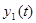 :
:
|
|
(2) |
где 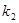 > 0 – коэффициент, также зависящий от индивидуальных особенностей.
> 0 – коэффициент, также зависящий от индивидуальных особенностей.
Таким образом, учащийся тем быстрее приобретает умения, чем больше он уже знает и умеет; чем больше умеет, тем быстрее усваивает новые знания. В то же время заметим, что на правую часть уравнения (1) влияют только приобретенные в прошлом активные знания, примененные при решении задач и перешедшие в умения.
Задача заключается в поиске такого управления 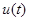 из отрезка [0;1], которое обеспечит получение максимального объема знаний за заданный промежуток времени T. Сделаем замену переменных:
из отрезка [0;1], которое обеспечит получение максимального объема знаний за заданный промежуток времени T. Сделаем замену переменных: 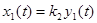 ,
, 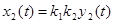 . В результате перейдем к системе, не содержащей неизвестных коэффициентов:
. В результате перейдем к системе, не содержащей неизвестных коэффициентов:
|
|
(3) |
Таким образом, задача об управлении процессом обучения формализуется в виде задачи оптимального управления:
|
|
(4) |
|
при динамических ограничениях: |
|
|
|
(5) |
|
ограничениях на управление: |
|
|
|
(6) |
|
и граничных условиях: |
|
|
|
(7) |
|
|
|
Разобьем равномерно отрезок 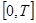 точками
точками 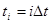 ,
, 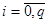 , полагая
, полагая 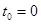 ,
, 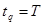 ,
, 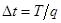 ,
, 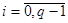 . Обозначим
. Обозначим 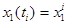 ,
, 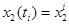 ,
, 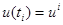 . Используем формулы Эйлера аппроксимации производных:
. Используем формулы Эйлера аппроксимации производных: 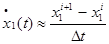 ,
, 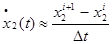 ,
, 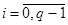 . Для вычисления интеграла в целевом функционале используем формулу левых прямоугольников.
. Для вычисления интеграла в целевом функционале используем формулу левых прямоугольников.
Дискретная задача, аппроксимирующая (4)-(7) с точностью 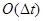 , имеет вид:
, имеет вид:
|
|
(8) |
Введем функцию
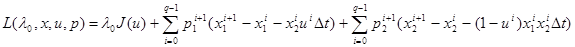
Из необходимых условий оптимальности L - функции получаем рекуррентные соотношения для вычисления импульсов, что позволяет сформулировать следующее утверждение.
Теорема.Пусть 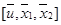 – локально оптимальное решение задачи (8), тогда
– локально оптимальное решение задачи (8), тогда 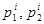 определяются по формулам:
определяются по формулам:
|
|
(9) |
производная L-функции по управлению 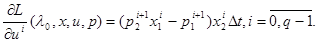
С использованием метода проекции градиента с учетом формул (9) построено решение задачи при выборе параметров: 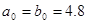 , q=1000, T=1. Результаты численных расчетов приведены на рис.1-3, оптимальное значение функционала
, q=1000, T=1. Результаты численных расчетов приведены на рис.1-3, оптимальное значение функционала 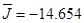 , количество итераций метода
, количество итераций метода 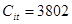 .
.
|
|
|
|
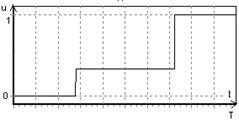
Рис. 1 - График |
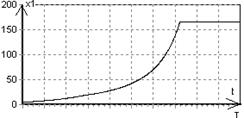
Рис. 2 - График |
|
|
|
|
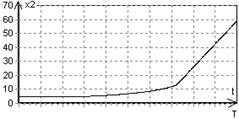
Рис. 3 - График |
|
Результаты, полученные численно, вполне соответствуют эмпирическим представлениям об оптимальной организации учебного процесса. Модель определяет численные значения доли времени u(t), идущей на повышение знаний, и доли материала (1-u(t)), излагаемого на заключительных лекциях без проработки на семинарах.
Литература:
1. Евтушенко Ю.Г. Методы решения экстремальных задач и их применение в системах оптимизации. М.: Наука, 1982.
2. Неуймин Я.Г. Модели в науке и технике. История, теория, практика. - Л.: Наука, 1984. - 190 с.
3. Моисеев Н.Н. Математические задачи системного анализа. - М.: Наука, 1981. - 488с.
4. Орлов А.И. Устойчивость в социально-экономических моделях. - М.: Наука, 1979. -296с.
5. Орлов А.И. Математические модели отдельных сторон обучения математике. – В: «Сб. научно-методических статей по математике. (Проблемы преподавания математики в вузах.)» Вып.7. - М.: Высшая школа, 1978. С.28-34.
6. Гольштейн Е.Г. Выпуклое программирование (элементы теории). – М.: Наука, 1970. Болтянский В.Г. Математические методы оптимального управления. – М.: Наука, 1969.







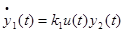 ,
,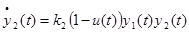 ,
,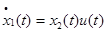 ,
, 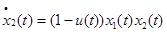 .
.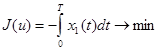 ,
,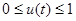 ,
, 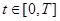 ,
,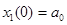 ,
, 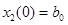 .
.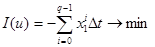 ,
,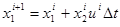 ,
, 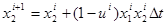 ,
, 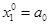 ,
, 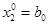
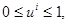
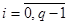 .
.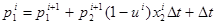 ,
,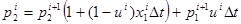 ,
, 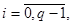
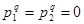 .
.