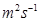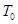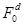В работе рассматриваются метод и диалоговое программное обеспечение, позволяющие оптимизировать по различным критериям процесс стерилизации продуктов питания в промышленных автоклавах. Рассматриваемый метод базируется на численном решении одной задачи оптимального управления для уравнения теплопроводности. В качестве основного алгоритма оптимизации используется зарекомендовавший себя на практике адаптивный случайный поиск. Разработанные и адаптированные под особенности решаемой задачи диалоговые средства делают рассматриваемый в статье метод легкодоступным для практического применения.
Ключевые слова: автоклав, стерилизация продуктов питания, оптимизация, диалоговое программное обеспечение.
1. Введение
Тепловая стерилизация в автоклавах остается по настоящий день наиболее распространенной и эффективной технологией, применяемой для консервирования продуктов питания [1]. В изготовлении консервов процесс тепловой стерилизации является самым главным и ответственным, так как от того, насколько корректно выполнена стерилизация, зависят: стойкость консервов при длительном хранении, качество итогового продукта или его пищевая ценность, и экономическая эффективность самого процесса стерилизации. Некорректно выполненная стерилизация с одной стороны может привести к тому, что в исходном продукте будут уничтожены не все вредоносные микроорганизмы, а с другой, привести к существенному разрушению основных питательных компонентов продукта [1,2,15]. Именно поэтому, очень важно при изготовлении консервов придерживаться так называемых режимов стерилизации, обеспечивающих как безопасность к употреблению получаемого продукта в течение установленного гарантией срока, так и необходимое содержание в продукте основных его питательных компонентов [1,2].
Стерилизация консервов выполняется в автоклавах, представляющих собой аппараты закрытого типа. Автоклавы бывают двух типов — вертикальные и горизонтальные. Наибольшее распространение в консервной промышленности получили вертикальные автоклавы, так как в них можно стерилизовать все виды консервов в жестяной и стеклянной таре. Весь процесс стерилизации можно разделить на несколько следующих этапов:
Этап 1. Загрузка; в автоклав заливается холодная вода, которая подогревается до некоторой заданной начальной температуры. При достижении заданной температуры в автоклав опускается продукция, и его крышка герметично закрывается.
Этап 2. Тепловая обработка; продукт подвергается тепловой обработке согласно выбранному процессу стерилизации. Процесс стерилизации определяет используемую для стерилизации температуру и время, в течение которого эта температура выдерживается.
Этап 3. Охлаждение; для плавного остывания в автоклав подают воду определенной температуры. На этом процесс стерилизации завершается.
Расчеты режимов стерилизации выполняются на базе различных эмпирических закономерностей, наиболее важными среди которых являются закономерности между количеством жизнеспособных вредоносных микроорганизмов и используемыми параметрами нагрева продукта [1,2,15]. Следующими по важности могут идти закономерности между параметрами нагрева и пищевой ценностью продукта. Таким образом, корректно подобранный режим стерилизации должен обеспечивать требуемую степень летальности процесса, т. е. отмирание существенной части вредоносных микроорганизмов, и при этом − не привести к значительному ухудшению органолептических показателей продукта, т.е. обеспечить требуемую пищевую ценность.
Режим стерилизации можно определить как следующую четверку:
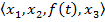 ,
,
где 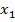 – время необходимое для повышения температуры в автоклаве до некоторой начальной температуры стерилизации,
– время необходимое для повышения температуры в автоклаве до некоторой начальной температуры стерилизации, 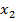 – продолжительность процесса стерилизации,
– продолжительность процесса стерилизации, 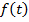 – функция, выражающая зависимость температуры стерилизации от времени,
– функция, выражающая зависимость температуры стерилизации от времени, 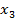 – длительность снижения температуры от конечной температуры стерилизации до некоторой константной температуры. В случае если
– длительность снижения температуры от конечной температуры стерилизации до некоторой константной температуры. В случае если 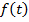 тождественно равна некоторой константе, то такой режим стерилизации в этой работе будет называться константным, иначе режим стерилизации будет называться вариабельным.
тождественно равна некоторой константе, то такой режим стерилизации в этой работе будет называться константным, иначе режим стерилизации будет называться вариабельным.
В пищевой промышленности для стерилизации консервов широко используются константные режимы стерилизации, так как они сравнительно проще в реализации. Однако, как показали многочисленные исследованиями, выполненные в том числе в работах [3−14], использование вариабельных режимов стерилизации позволяет в некоторых случаях значительно увеличить экономическую эффективность процесса стерилизации, обеспечивая при этом необходимый уровень летальности итогового продукта и не ухудшая его пищевой ценности (как правило, качество итогового продукта в этом случае улучшается). Увеличение экономической эффективности в этом случае достигается в основном за счет уменьшения времени функционирования стерилизационной установки. Использование вариабельных режимов позволяет более эффективно решать однокритериальные [3−8,9,10,11,13] и многокритериальные задачи оптимизации процесса стерилизации [8,12,14].
В настоящей работе рассматривается метод, использующий вариабельные режимы стерилизации для оптимизации по различным критериям процесса стерилизации продуктов питания в промышленных автоклавах [3−14]. Рассматриваемый метод базируется на численном решении одной задачи оптимального управления для уравнения теплопроводности. В качестве основного алгоритма оптимизации используется зарекомендовавший себя на практике адаптивный случайный поиск (СП) [11,13,14]. В этой работе предполагается, что подготовленные к стерилизации продукты питания упакованы в цилиндрические контейнеры. Для рассматриваемого метода автором была разработана программная система “OPT-PROx” (OPTimal PROfile), диалоговый интерфейс и функциональные возможности которой были адаптированы под особенности используемого метода. Это делает рассматриваемый в статье подход легкодоступным для применения на практике.
2. Стерилизующий эффект и пищевая ценность
Следующее выражение используются в консервной промышленности для подсчета величины стерилизующего эффекта (или степени летальности) [1,2,15]:
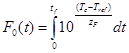 , (1)
, (1)
где 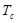 – температура в критической точке контейнера (точка, для которой в процессе стерилизации наблюдается наименьший нагрев продукта),
– температура в критической точке контейнера (точка, для которой в процессе стерилизации наблюдается наименьший нагрев продукта), 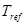 – эталонная температура, которая в большинстве случаев берется равной 121.1°C,
– эталонная температура, которая в большинстве случаев берется равной 121.1°C, 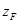 – константа термоустойчивости микроорганизмов (берется равной 10°C),
– константа термоустойчивости микроорганизмов (берется равной 10°C), 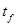 – время, затраченное на стерилизацию.
– время, затраченное на стерилизацию.
Несколько критериев используется в консервной промышленности для определения качества (пищевой ценности) получаемого продукта [1,2,15]. В настоящей работе будет использоваться следующий интегральный критерий, характеризующий среднюю потерю витаминов в получаемом продукте:
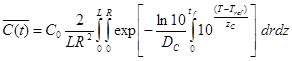 , (2)
, (2)
где T – температура внутри контейнера, 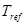 – эталонная температура, которая в большинстве случаев берется равной 121.1°C,
– эталонная температура, которая в большинстве случаев берется равной 121.1°C, 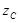 – константа термоустойчивости витаминов,
– константа термоустойчивости витаминов, 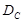 – количественная характеристика скорости процесса разрушения витаминов,
– количественная характеристика скорости процесса разрушения витаминов, 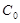 – константа, равная 100,
– константа, равная 100, 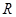 – радиус контейнера,
– радиус контейнера, 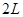 – диаметр контейнера,
– диаметр контейнера,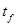 – время, затраченное на стерилизацию.
– время, затраченное на стерилизацию.
Использование в выражении (2) соответствующих значений для констант 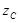 и
и 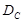 позволяет вычислять значения других интегральных критериев пищевой ценности, например критерий, характеризующий степень разрушения ферментов [1,2,15].
позволяет вычислять значения других интегральных критериев пищевой ценности, например критерий, характеризующий степень разрушения ферментов [1,2,15].
3. Постановка задачи
Процесс прохождения тепла сквозь контейнер, наполненный некоторым продуктом, можно описать с помощью следующего уравнения теплопроводности в цилиндрических координатах [15]:
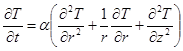 , (3)
, (3)
со следующими граничными и начальными условиями:
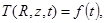
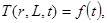
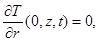 (4)
(4)
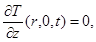
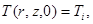
где 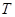 – температура, t – время,
– температура, t – время, 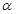 – коэффициент теплопроводности продукта,
– коэффициент теплопроводности продукта, 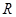 – радиус контейнера,
– радиус контейнера, 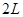 – диаметр контейнера,
– диаметр контейнера, 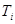 – начальная температура продукта,
– начальная температура продукта,  – функция, выражающая зависимость температуры стерилизации от времени
– функция, выражающая зависимость температуры стерилизации от времени 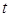 ,
, 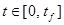 .
.
Таким образом, для оптимизации процесса стерилизации необходимо найти функцию  , доставляющую минимум некоторому функционалу, характеризующему эффективность проводимой стерилизации.
, доставляющую минимум некоторому функционалу, характеризующему эффективность проводимой стерилизации.
Следующие однокритериальные и многокритериальные задачи оптимизации процесса стерилизации уже рассматривались в работах других авторов.
Однокритериальные задачи
1) Максимизация пищевой ценности продукта при наличии ограничений на уровень летальности итогового продукта [3,4,11,13].
2) Минимизация времени стерилизации при наличии ограничений на уровни пищевой ценности и летальности итогового продукта [5,7,9,11,13].
3) Минимизация времени стерилизации при наличии ограничений на уровни пищевой ценности и летальности итогового продукта, а также – на количество энергии, затрачиваемой стерилизационной установкой [6].
Многокритериальные задачи
1) В работах [12,14] решены задачи оптимизации по двум различным критериям, отражающим качество итогового продукта, и по времени, затрачиваемому на процесс стерилизации.
2) В работе [8] решена задача оптимизации для случая, когда в одном автоклаве одновременно стерилизуются продукты в контейнерах двух различных типов, при этом обеспечивается режим стерилизации, удовлетворяющий заданным ограничениям для пищевой ценности и летальности итогового продукта.
В настоящей работе приведены примеры решения однокритериальных задач 1 и 2.
4. Метод решения
Сформулированные выше задачи оптимального управления успешно решаются численно путем ограничения класса управлений параметрическим семейством функций с последующей редукцией задачи отыскания экстремума функционала к задаче отыскания экстремума функции многих переменных. В работах [4−9] использовались кусочно-постоянные и кусочно-линейные управления, при этом размерность многоэкстремальной задачи оптимизации, полученной после редукции, достигала 50-60. В работе [10] авторы использовали для поиска оптимального управления функции sin и exp, получая результаты уступающие результатам кусочно-постоянных и кусочно-линейных аппроксимаций. В работах [11,13,14] в качестве управлений использовались кубические сплайны, что позволило значительно сократить размерность решаемой многоэкстремальной задачи оптимизации (до 5-7 переменных), получая при этом результаты, характерные для кусочно-постоянных и кусочно-линейных аппроксимаций.
В качестве метода оптимизации в этой работе используется зарекомендовавший себя на практике адаптивный случайный поиск [11,13,14], а также − некоторые его модификации, позволяющие в некоторых случаях улучшить адаптивные свойства СП и, тем самым, сократить количество вычислений целевой функции, необходимых для получения приемлемого решения. Последний факт является важным, так как краевая задача, определяемая выражениями (3) и (4), решается в этой работе конечно-разностным методом, и, для некоторых случаев, однократное вычисление целевой функции может занимать от 30 секунд до 60 секунд компьютерного времени.
4.1.Описание адаптивного случайного поиска
|
|
|
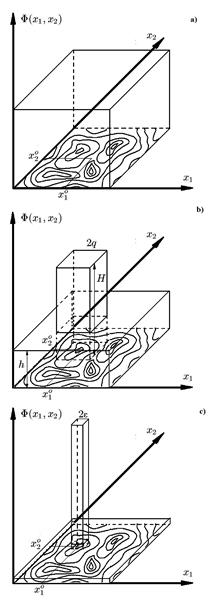
Рисунок 1. Пример изменения вида функции плотности вероятности распределения для двух переменных |
Далее приведем краткое описание используемого в работе адаптивного случайного поиска. Организацию процесса случайного поиска в общем виде можно представить следующим образом. Поиск разбивается на некоторое число шагов. На каждом шаге по определенному закону случайным образом выбираются значения вектора аргументов целевой функции, и подсчитывается значение целевой функции. На каждом шаге СП закон, по которому выбираются значения переменных изменяется таким образом, чтобы вероятность попадания в ε-окрестность истинного минимума увеличилась бы. Для этого используется информация, полученная на предыдущих шагах поиска. Не нарушая общности, можно сказать, что адаптацию СП под особенности целевой функции обеспечивает уменьшение дисперсии разброса вокруг точки наиболее предполагаемого нахождения оптимума. На рисунке 1 показано как изменяется вид функции плотности вероятности распределения для двух переменных в зависимости от количества шагов случайного поиска. На первом шаге СП, когда нет никакой информации о положении минимума, поиск ведется с равномерной плотностью распределения по всей области определения целевой функции (см. рис. 1a.). В процессе поиска происходит накопление информации о характере поведения функции цели, и вид функции плотности изменяется таким образом, что наиболее интенсивно поиск осуществляется в области предполагаемого расположения минимума целевой функции (см. рис. 1b). На заключительных шагах функция плотности распределения вырождается в дельта-функцию (см. рис 1c). Более подробно с алгоритмом случайного поиска можно ознакомиться в работах [11,13,14].
5. Полученные результаты
В таблице 1 приведены параметры, используемые далее в численных экспериментах. Следующие предварительные расчеты будут необходимы для демонстрации результатов оптимизации с использованием вариабельных режимов. На рисунке 2 изображена кривая, каждая точка которой определяет температуру и продолжительность стерилизации, необходимые для получения итогового продукта с минимально требуемым уровнем летальности. В свою очередь, для каждой точки кривой, изображенной на рис. 2 было подсчитано значение критерия качества продукта (2). Полученная таким образом кривая представлена на рисунке 3. Из рисунка 3 видно, что константный режим стерилизации обеспечивает максимально возможный уровень качества продукта, равный 53%. Как видно из рисунка 2 этот уровень стерилизации обеспечивается температурой стерилизации – 118 °C и продолжительностью стерилизации, равной 98 мин.
Таблица 1. Параметры, используемые в численных экспериментах.
|
Радиус R |
0.04375 |
|
Высота 2L |
0.1160 |
|
Коэффициент теплопроводности продукта |
1.5443× |
|
Начальная температура продукта |
71.0 °C |
|
Наименование микроорганизмов |
Baccillus stearothermophilus |
|
|
10 °C |
|
|
121.1 °C |
|
Используемый критерий качества продукта |
Средняя потеря витаминов |
|
|
25.56 °C |
|
|
178.6 min. |
|
|
121.11 °C |
|
Минимально необходимый уровень летальности |
8 min. |
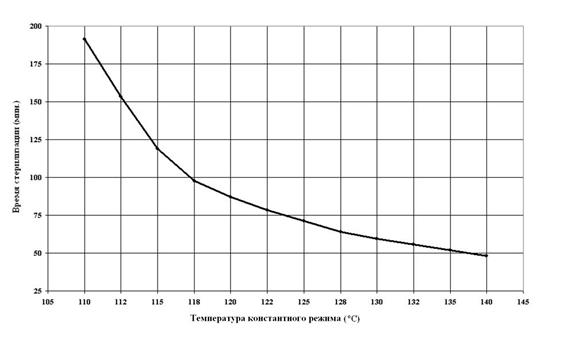
Рисунок 2. Кривая определяющая зависимость продолжительности стерилизации от температуры стерилизации.
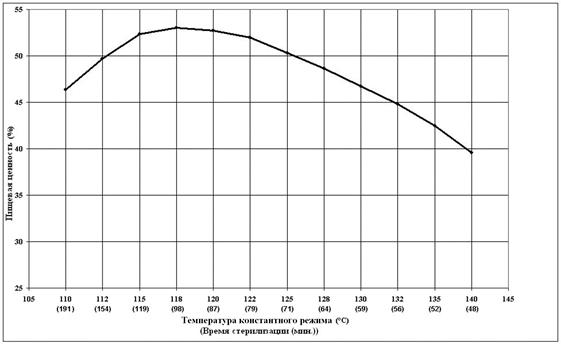
Рисунок 3. Кривая определяющая зависимость уровня пищевой ценности от продолжительности и температуры стерилизации.
5.1.Задача максимизации пищевого качества продукта
На рисунке 4 приведены полученные после 600 итераций адаптивного случайного поиска температурные кривые автоклава и критической точки контейнера. Уровень качества продукта при этом составил 55% против 53% обеспечиваемых константным режимом стерилизации, а продолжительность стерилизации – 89 мин., что на 9 минут меньше продолжительности соответствующего константного режима (см. рис. 3). Таким образом, вариабельный режим стерилизации обеспечил получение итогового продукта более высокого качества и за меньшее время стерилизации.
5.2.Задача минимизации времени стерилизации
В задаче минимизации времени стерилизации был выбран 50% уровень минимально возможного качества итогового продукта. Полученные после 700 итераций случайного поиска температурные кривые представлены на рис. 5. Продолжительность вариабельного режима стерилизации составила 65 мин., что на 5 минут меньше времени соответствующего константного режима стерилизации, т.е. режима, обеспечивающего 50% уровень качества продукта (см. рис. 3).
Рисунок 4. Температурные кривые автоклава и критической точки контейнера, соответствующие найденному оптимальному режиму стерилизации для задачи максимизации пищевого качества продукта.
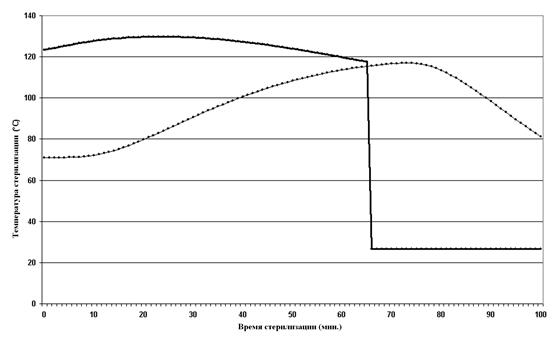
Рисунок 5. Температурные кривые автоклава и критической точки контейнера, соответствующие найденному оптимальному режиму стерилизации для задачи минимизации продолжительности процесса стерилизации.
6. Описание диалоговой программной системы “OPT-PROx”
Диалоговая программная система “OPT-PROx” полностью реализует описанный выше подход к решению задач оптимизации процесса стерилизации. Программная система содержит следующие две рабочие вкладки (см. рис. 6):
· “Thermaldiffusivityestimation”: ориентирована на вычисление коэффициента теплопроводности продукта; процедура вычисления коэффициента теплопроводности базируется на использовании температурных кривых автоклава и критической точки контейнера, полученных экспериментально (температурная кривая автоклава используется для решения приведенной выше краевой задачи, а температурная кривая критической точки контейнера − для подсчета значения критерия, определяющего близость текущего коэффициента теплопроводности, подбираемого случайным поиском, к истинному).
· “Thermalprocessingoptimization”: ориентирована на решение однокритериальных задач оптимизации процесса стерилизации при наличии ограничений на уровни пищевой ценности и летальности итогового продукта.
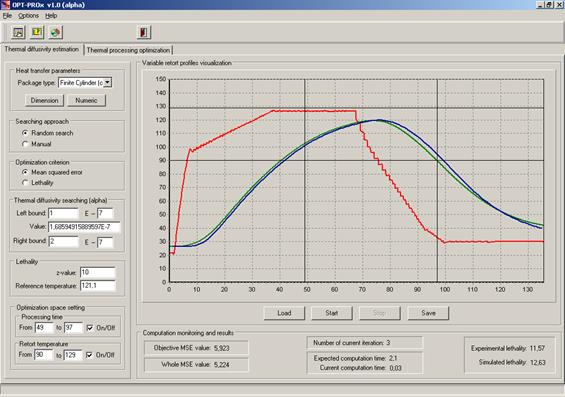
Рисунок 6. Главное окно программной системы “OPT-PROx” и две ее основные рабочие вкладки: “Thermal diffusivity estimation” и “Thermal processing optimization”.
Далее рассмотрим эту вкладку более подробно. Группы диалоговых элементов, объединенных наименованиями “Heat transfer parameters”, “Retort temperature”, “Come-up time” и “Cooling” предназначены для параметризации используемой конечно-разностной схемы и вариабельного режима стерилизации (см. рис. 7). Группа диалоговых элементов “Thermal process lethality and quality parameters” предназначена для ввода констант, используемых для подсчета стерилизующего эффекта и критериев качества (пищевой ценности). Группа элементов “Optimization problem definition” позволяет пользователю сформулировать свою задачу оптимизации, выбрав из предоставленного списка требуемую целевую функцию и пометив необходимые ограничения. В правой части вкладки “Thermal processing optimization” расположены средства визуализации получаемого решения, позволяющие пользователю контролировать процесс оптимизации.
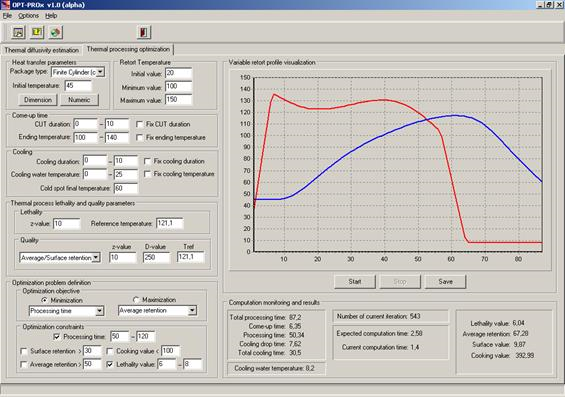
Рисунок 7. РHРРР Рабочая вкладка “Thermal processing optimization” и ее диалоговые элементы.
Программная система “OPT-PROx” снабжена файлом-справкой, достаточной для ознакомления со всеми ее возможностями, неупомянутыми в настоящей работе.
7. Заключение
Рассмотренный в работе метод позволяет повысить эффективность процесса стерилизации продуктов питания в промышленных автоклавах. Разработанная диалоговая система “OPT-PROx” делает представленный метод легкодоступным для практического применения.
Литература:
1. Флауменбаум Б.Л. Основы консервирования пищевых продуктов.- М.: Легкая и пищевая промышленность, 1982,- 267 с
2. Бабарин В.П. Стерилизация консервов: Справочник. СПб. : ГИОРД, 2006. – 306
3. Teixeira A, Dixon J, Zahradnik J, Zinsmeister G. (1969). Computer optimization of nutrient retention in thermal processing of conduction-heated foods. Journal of Food Technology 23(6):137–42.
4. Teixeira A, Zinsmeister G, Zahradnik J. (1975). Computer simulation of variable retort control and container geometry as a possible means of improving thiamine retention in thermally-processed foods. Journal of Food Science 40(3):656–9.
5. Banga, J. R., Perez-Martin, R. I., Gallardo, J. M., & Casares, J. J. (1991). Optimization of thermal processing of conduction-heated canned foods: Study of several objective functions. Journal of Food Engineering, 14, 25–51.
6. Almonacid-Merino, S. F., Simpson, R., & Torres, J. A. (1993). Time variable retort temperature profiles for cylindrical cans: Batch process time, energy consumption, and quality retention model. Journal of Food Process Engineering, 16, 271–287.
7. Balsa-Canto, E., Banga, J. R., & Alonzo, A. A. (2002). A novel, efficient and reliable method for thermal process design and optimization. Part II: Applications. Journal of Food Engineering, 52, 235–247.
8. Erdogdu, F., Balaban, M. 2003. Nonlinear constrained optimization of thermal processing. II. Variable process temperature profiles to reduce process time and to improve nutrient retention in spherical and finite cylindrical geometries. Journal of Food Process Engineering. 26(3), 303-314.
9. Garcia, M. S. G., Balsa-Canto, E., Alonso, A. A., & Banga, J. R. (2005). Computing optimal operating policies for the food industry. Journal of Food Engineering, 74(1), 13–23.
10. Chen C, Ramaswamy H. 2002. Modeling and optimization of variable retort temperature (VRT) thermal processing using coupled neural networks and genetic algorithms. Journal of Food Engineering 53(3):209–20.
11. Simpson R., Abakarov A., and Teixeira A. Variable retort temperature optimization using adaptive random search techniques. Journal of Food Control 19 (2008) 1023–1032.
12. Sendin, J. O. H., Alonso, A. A., & Banga, J. R. (2010). Efficient and robust multi-objective optimization of food processing: A novel approach with application to thermal sterilization. Journal of Food Engineering 98(3):317-324.
13. Abakarov A., Sushkov, Yu., Almonacid S., Simpson R. Thermal processing optimization through a modified adaptive random search. Journal of Food Engineering, 93(2), 200-209.
14. Abakarov, A., Sushkov, Y., Almonacid, S., Simpson, R. Multi-objective optimization based on adaptive random search method: optimization of food processing. Journal of Food Science, 74(9), E471 - E487.
15. Holdsworth, S., Simpson. 2007. Thermal Processing of Packaged Foods, 2nd Ed., Springer, New York.