Использование байесового сетевого подхода для управления транспортным потоком

В статье рассмотрен алгоритм построения Байесовой сети, на основании которой в дальнейшем предполагается управлять транспортным потоком.

To control traffic flow Bayesian network consists of nodes and directional causality between variables. Each node has a finite set of mutually exclusive states. Directed edges represent the causal relationship between variables. Tops and directed bonds form a directed graph without cycles.

В настоящее время развитие транспортной сети и увеличение количества автомобилей сделало актуальной задачу создания автоматизированной системы дорожного движения (АСУ ДД), которая бы осуществляла функции контроля дорожной ситуации и управления транспортным потоком. В решения этой задачи для мониторинга состояний и свойств сложных объектов не­прерывном изучении свойств и характеристик этих объектов путем обобщения прошлого опыта работы и вновь поступающей информации с позиций измерительного подхода, принципиальную основу кото­рого составляет метрологическое обоснование получаемых решений в данной работе предлагается использование байесового сетевого подхода. Новые знания, получаемые в ходе такого измерительного процесса, объединяются с массивами прошлых и служат априорной информацией для будущих экспериментов мониторинга. Байесова сеть для управления транспортным потоком состоит из вершин и направленных причинно-следственных связей между переменными. Каждая вершина имеет конечное множество взаимоисключающих состояний. Направленные рёбра отражают причинно-следственную связь между переменными. Вершины и направленные связи образуют ориентированный граф без циклов. Для каждой переменной А с родителями В₁….В_n задаётся таблица условных вероятностей Р (А|В₁…., В_n), численно выражающая причинную связь между ними. На рис. 1 показан пример байесовой сети.

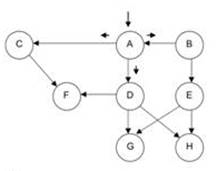
Рис. 1 Байесова сеть

Допустим, что U – пространство переменных. Предположим, что мы имеем беспрепятственный доступ к P(U), объединённой таблице вероятностей, тогда распределение вероятностей Р(А) для любой переменной А из U можно легко вычислить при помощи маргинализации.

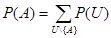                                                                       (1)

Байесова сеть на U - это более компактное представление P(U), т.е., это способ хранения информации, исходя из которой, при необходимости можно вычислить P(U). Допустим, что BN - Байесова сеть на основе U = {A₁, …A_n}. Если условные независимости в BN действительны и для U, тогда P(U) является результатом произведения всех условных вероятностей, заданных в BN [14].

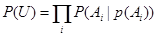        (2)

где pa(A_i) – это родительский комплект A_i, а pa(A_i|  pa(A_i)) – наше априорное знание об A_i в U.

Допустим, что А – переменная в U с n состояниями. Вывод  f  по A – это n-мерная таблица нулей и единиц. Способ введения f в BN можно представить как перемножение Рa(А) с таблицей f, в результате чего получается Рa(А,е), где е – это свидетельство того, что в вершине произошло некоторое событие.

Используя уравнение (1) и обновлённое распределение вероятностей P(U|e), можно вычислить апостериорное распределение вероятностей любой переменной А в U, P(A|e).

Для построения таблицы условных вероятностей байесовой сети, сеть делится на несколько кластеров, которые содержат пары узлов родитель-дочка. В каждом кластере узлов из каждого элемента знания, касающегося взаимоотношений между определённым параметром дорожного движения и событиями, относящимися к состоянию движения, составляется субъективные правила движения. Наконец, этим правилам присваиваются численные значения, и они преобразуются в элементы таблицы условной вероятности, которые прикрепляются к узлам данного кластера. Важным моментом в управлении потоком является выбор пороговых значений параметров дорожного движения (интенсивности движения, заполненность определённого пространства и скорость). Пороговые величины используются для определения состояний параметров дорожного движения.

Прозрачность байесовой сети обеспечивает полный доступ к её таблицам условных вероятностей. Путём обновления определённых элементов байесовой сети можно на любой стадии эффективно учесть любые изменения условий дорожного движения. Эта особенность может рассматриваться как субъективное обучение сети, а выбор пороговых величин параметров дорожного движения как субъективная оценка конкретных обстоятельств дорожного движения.

Литература

1. Woolley, J.E., Taylor, M.A.P., Zito, R., 2001. Modelling of the Southern Expressway using Paramics mirosimulation software. Journal of the Eastern Asia Society for Transportation  Studies 4 (4), 279–295.
2. Zhang, K., Taylor, M.A.P., 2002. Automated incident detection – Bayesian networks approach. In: Proceedings of the 24th Conference of Australian Institutes of Transport Research, Sydney.
3. Zhang, K., Taylor, M.A.P., 2004. Incident detection on freeways: a Bayesian network approach. In: Proceedings of the 27th Australasian Transport Research Forum, Adelaide.
4. Thomas, K., Dia, H., Cottman, N., 2001. Simulation of arterial incident detection using neural networks. In: 8th World Congress on ITS,Sydney.
5. Woolley, J., Dyson, C., Taylor, M.A.P., 2001. Evaluation of a South Australian 40 km/h urban speed limit. Transport Engineering in Australia 7 (1–2).
6. Yuan, F., Cheu, R.L., 2003. Incident detection using support vector machines. Transportation Research C 11, 309–328.