Введение
В настоящее время, все большее значения принимают вопросы энергетической эффективности летательных аппаратов, в том числе беспилотных. Один из путей к этой цели, повышение аэродинамического качества летательного аппарата. Существенную долю в аэродинамическом сопротивлении и главенствующую в подъемной силе самолета играет крыло, а точнее, если не брать в расчет качество поверхности, форма профиля. Существующая ныне тенденция применения аэродинамических форм переменного профиля, исключает возможность использования параметров из атласа профилей. Это приводит к необходимости экспериментального или расчетного определения требуемых параметров. Провидение натурных экспериментов весьма затратно в финансовом и временном плане. Использование программных продуктов для численного моделирования требует их идентификации под конкретные задачи.
Закономерно, что по мере прогресса авиационной техники задачи отработки авиационных профилей менялись. В настоящее время большинство проводимых экспериментальных, теоретических и численных исследований такого характера направлено в основном на изучение обтекания крыльев в диапазоне чисел Маха, при которых в потоке имеют место значительные эффекты сжимаемости, что не характерно для большей части частной авиации и беспилотных летательных аппаратов. Однако имеется значительное количество экспериментальных данных, накопленных в 30-50 годы прошлого столетия, которые рассматривают задачи нахождения силовых характеристик и оптимизации обтекания аэродинамически профилированных крыльев при малых числах Маха, когда газ можно полагать полностью несжимаемой. К таким исследованиям относится и продувка профиля NACA-2406, выполненная лабораторией LMAL – NASA в трубе переменной плотности в 1931 году. Результаты эксперимента были опубликованы в нашей стране в сборнике [1].
Изучение обтекания крыла с подобной профилировкой потоком несжимаемой жидкости сегодня не потеряло своей актуальности в задачах проектирования морских гребных винтов. Обтекание лопасти гребного винта во многом подобно обтеканию крыла конечного размаха. Аэродинамические профили, в том числе NACA-2406, находят применение при профилировании лопастей некавитирующих гребных винтов, так как их гидродинамические качества способствуют получению высоких коэффициентов полезного действия. Поэтому численное моделирование обтекания подобных авиационных профилей является важным для изучения гидродинамики гребных винтов и может рассматриваться как шаг на пути решения более сложной задачи численного моделирования их работы.
Задачи идентификации была решена для обтекания профиля NASA-2406 потоком воздуха при различных углах атаки: 1-10° с шагом 1° и 10-45° с шагом 5° с использованием CAE системы ANSYS CFX 11. По результатам численного моделирования проводилось сравнение коэффициентов Cy, Cx с результатами натурного эксперимента [1] и оценивалась точность расчета.
1 Исходные параметры
Профиль NACA-2406 (рис. 1) имеет следующие геометрические характеристики:
− относительная толщина с = 0,06
− относительная вогнутость f = 0,20;
− относительное положение максимальной вогнутости fx = 0,40.

Рисунок 1 – Профиль NASA-2406
Использованный в работе, эксперимент выполнен в трубе переменной плотности диаметром 1.52 м (критическое число Рейнольдса 150000) на прямоугольной модели крыла размерами 127 × 762 мм (λ=6). Скорость набегающего потока в эксперименте составляла 21.1 м/с, Re = 3120000, M = 0.06.
2 Численное моделирования в среде ANSYS CFX
Численное моделирование в CAE системах, в т. ч. и в ANSYS CFX можно разделить на следующие этапы.
1. Создание геометрической модели.
2. Импортирование геометрии в CAE систему (DesignModeler).
3. Генерация расчетной сетки (приложение Meshing, метод CFX-Mesh) (рис 2).
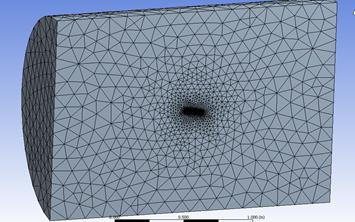
Рисунок 2 – Сформированная нерегулярная тетраэдрическая сетка с измельчением сетки у поверхности крылового профиля
4. Импортирование сетки в препроцессор (ANSYS CFX-Pre).
5. Задание граничных и начальных условий в препроцессоре (рис 3).
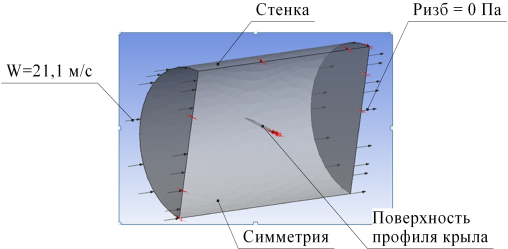
Рисунок 3 – Граничные условия
6. Расчет варианта в расчетном процессоре (ANSYS CFX-Solver).
7. Визуализация и анализ результатов расчета в постпроцессоре (ANSYS CFX-Post)
В CFX-Mesh – использовалась нерегулярная тетраэдрическая сетка.
Размер исходной сетки во всей расчетной области выбран 100 мм (ребро тетраэдра). Минимальный и максимальный размер ребра тетраэдра на всех поверхностях расчетной области, за исключением отдельных поверхностей, на которых задано измельчение сетки с учетом особенностей течения, соответственно, 5 и 100 мм.
На поверхности крыла задавалось измельчение сетки – постоянный размер ячейки 3 мм, радиус инфляции (распространения) 6 мм. Высота исходной призмы 0,3 мм, коэффициент увеличения высоты призмы 1,2.
Модель жидкости несжимаемая, течение турбулентное, модель турбулентности k-e.
Параметры турбулентности: интенсивность турбулентности 0,03, масштаб турбулентности 0,005 м.
Стенка без проскальзывания, гладкая (имеется пограничный слой).
Вещество – воздух, подчиняется закону идеального газа.
Температура области – 288,15 К. Термодинамическая модель Isothermal.
Опорное давление – 1 атмосфера.
Была выполнена необходимая серия расчетов, сходимость оценивалась по среднеквадратичной невязке.
В качестве примера результата расчета, приведено распределение осевой скорости вблизи поверхности профиля при угле атаки 250 (рис. 4).
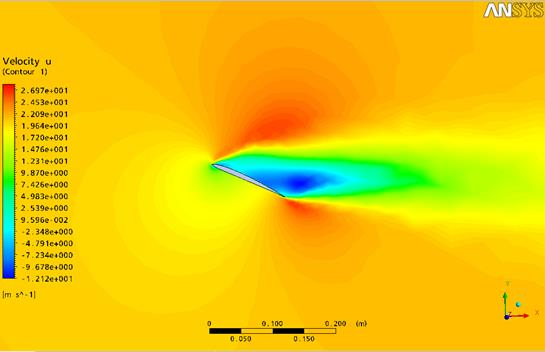
Рисунок 4 – Распределение осевой скорости при угле атаки 250
На рисунке хорошо видно отрыв потока и зону обратных токов за крылом.
По результатам численного моделирования были получены значения сил X и Y для различных углов атаки (таблица 1).
Таблица 1 – Значения сил X и Y
|
α, град |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
X, Н |
0,3049 |
0,2984 |
0,3331 |
0,3850 |
0,4533 |
0,5504 |
0,6645 |
0,8028 |
|
Y, Н |
1,7945 |
3,0348 |
4,0673 |
5,0830 |
6,0560 |
7,0022 |
7,9059 |
8,7191 |
|
8 |
9 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
|
1,0240 |
1,1572 |
1,4112 |
2,9148 |
4,5517 |
6,0606 |
7,5572 |
9,2267 |
10,818 |
12,372 |
|
9,4389 |
9,7943 |
10,146 |
11,128 |
12,133 |
12,593 |
12,779 |
13,004 |
12,823 |
12,371 |
Значения сил X и Y переведены в коэффициенты Сх и Су следующим образом:
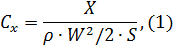
где 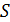 – площадь крыла, м2;
– площадь крыла, м2;
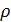 - плотность среды (воздуха), кг/м3;
- плотность среды (воздуха), кг/м3;
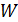 - скорость движения среды относительно профиля крыла, м/с.
- скорость движения среды относительно профиля крыла, м/с.
Площадь крыла
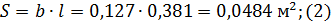
плотность среды 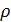 = 1,25 кг/м3;
= 1,25 кг/м3;
скорость потока воздуха 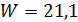 м/с.
м/с.
Произведение скоростного напора на площадь
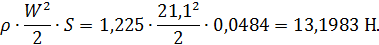
Значения сил X и Y были переведены в коэффициенты Сх и Су, результаты сведены в таблицу 2.
Таблица 2 – Значения коэффициентов Сх и Су для различных углов атаки
|
α, град |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Сх |
0,0231 |
0,0226 |
0,0252 |
0,0292 |
0,0343 |
0,0417 |
0,0503 |
0,0608 |
0,0776 |
|
Су |
0,1360 |
0,2299 |
0,3082 |
0,3851 |
0,4588 |
0,5305 |
0,5990 |
0,6606 |
0,7152 |
|
α, град |
9 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
|
Сх |
0,0877 |
0,1069 |
0,2208 |
0,3449 |
0,4592 |
0,5726 |
0,6991 |
0,8196 |
0,9374 |
|
Су |
0,7421 |
0,7688 |
0,8432 |
0,9192 |
0,9542 |
0,9682 |
0,9853 |
0,9715 |
0,9373 |
По результатам вычисления коэффициентов Сx и Cy был построен график зависимости коэффициентов лобового сопротивления и подъемной силы от угла атаки в случае численного и натурного экспериментов (рисунок 5) и проведено качественное сравнение этих результатов.
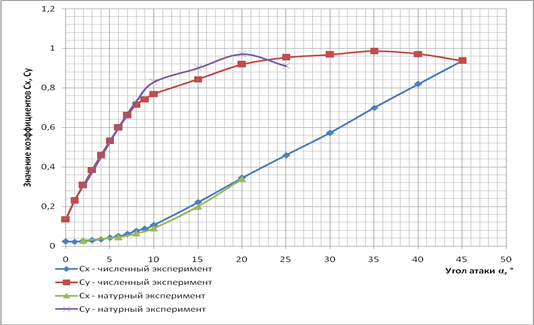
Рисунок 5 – Зависимость коэффициентов Сx и Cy от угла атаки α в численном и натурном экспериментах
Из рисунка 5 видно, что погрешность между численным и натурным экспериментом в Cy составляет не более 4% по отношению к абсолютному значению коэффициента подъемной силы в натурном эксперименте. Такое расхождение объясняется тем, что не были точно известны значения температуры, параметров турбулентности, при которых проводился натурный эксперимент.
Заключение
По результатам сравнения результатов численного трехмерного моделирования в ANSYS CFX с экспериментальными данными можно сделать вывод, что модели течения, используемые в ANSYS CFX, и методика применения данного пакета (в том числе формирование сетки, задание граничных условий, возможное упрощение геометрии) для решения задач аэродинамики крыла позволяют решать их с достаточной для практики точностью.
Работа выполнена при финансовой поддержке в рамках федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» на 2009-2013 годы.







