Неопределенность и риск являются неотъемлемыми свойствами инвестиционной деятельности компании. Инвестиционный проект разрабатывается базируясь на вполне определенных предположениях относительно капитальных и текущих затрат, объемов реализации произведенной продукции, цен на товары, временных рамок проекта. Вне зависимости от качества и обоснованности этих предположений будущее развитие событий, связанных с реализацией проекта, всегда неоднозначно. Это основная аксиома любой предпринимательской деятельности. Результат инвестирования средств во многом определяется тем, насколько полно выявлены настоящие и будущие сферы неопределенности и риска проекта. Эти сферы предопределяют величину прибыли инвестора, получаемой от вложенного им капитала.
Следует отметить, что неопределенность представляет более широкое понятие, чем риск, и отражает состояние неоднозначности развития событий в будущем, состояние нашего незнания и невозможности точного предсказания основных величин и показателей развития деятельности предприятия и в том числе реализации инвестиционного проекта. Неопределенность отражает множество возможных исходов, вероятности которых неизвестны, при этом инвесторы не имеют доступа к информации и оснований для расчета ожидаемых значений. Неопределенность – это объективное явление, которое с одной стороны является средой любой предпринимательской деятельности, с другой стороны – это причина постоянной «головной боли» любого предпринимателя. Однако неопределенность нельзя трактовать как исключительно негативное явление. В рыночной экономике неопределенность может сулить дополнительные возможности, которые не были видны в самом начале инвестиционного проекта, но в целом это явление оценивается со знаком «минус» в предпринимательской деятельности, поэтому можно и нужно учиться принимать решения в условиях неопределенности, так как в этом состоит залог успеха реализации инвестиционного проекта.
Риск, по своей природе, является измеряемой производной неопределенности и представляет множество возможных исходов, каждый из которых характеризуется определенной вероятностью. В этом случае инвесторы имеют доступ к информации и некоторые основания для оценки ожидаемых доходов. Это означает, что риск подлежит анализу, оценке и контролю со стороны инвестора.
При разработке и экспертизе инвестиционного проекта вопрос о его эффективности решается на основе анализа значений различных интегральных показателей – NPV, IRR, DPP, PI и др. Но все расчеты проводятся для базового варианта инвестиционного проекта, реализация которого, по мнению разработчиков, наиболее правдоподобна. В данной ситуации строится только одна модель прогнозных потоков денежных средств. И эта модель является моделью принятия решений в условиях определенности. В действительности, на практике нельзя быть полностью уверенным, что при реализации инвестиционного проекта все денежные потоки будут в точности соответствовать прогнозным. С момента реализации проекта на каждом этапе будет возникать все большее и большее расхождение между прогнозными и реальными денежными потоками. Может возникнуть ситуация, что задержки в оплате продукции, рост цен на материалы, изменение валютного курса, налоговых ставок или другие негативные события приведут к полному краху проекта или, как минимум, к существенным дополнительным издержкам. Возникают вопросы: Как оценить устойчивость проекта к изменениям внешней среды? Как количественно измерить риск, связанный со всем проектом в целом? Применение имитационного моделирования по методу Монте-Карло в инвестиционных расчетах позволяет ответить на эти вопросы.
Датой рождения метода Монте-Карло принято считать 1949 г., когда американские ученые Н. Метрополис и С. Улам опубликовали статью «Метод Монте-Карло», в которой систематически его изложили. Название метода связано с названием города Монте-Карло, где в игорных домах (казино) играют в рулетку – одно из простейших устройств для получения случайных чисел, на использовании которых основан этот метод. Область применения метода Монте-Карло достаточно широка. В качестве примеров можно привести расчет систем массового обслуживания, расчет качества и надежности изделий, вычисление определенного интеграла и др.
В общем случае имитационное моделирование Монте-Карло – это процедура, с помощью которой математическая модель определения какого-либо финансового показателя (в нашем случае NPV) подвергается ряду прогонов с помощью компьютера. В ходе процесса имитации строятся последовательные сценарии с использованием исходных данных, которые по смыслу проекта являются неопределенными, и потому в процессе анализа полагаются случайными величинами. Процесс имитации осуществляется таким образом, чтобы случайный выбор значений из определенных вероятностных распределений не нарушал существования известных или предполагаемых отношений корреляции среди переменных. Результаты имитации собираются и анализируются статистически, с тем, чтобы оценить меру риска.
Наличие хорошей исходной модели инвестиционного проекта – это необходимая база для проведения значимого, результативного имитационного моделирования.
Метод Монте-Карло, являясь одним из наиболее сложных методов количественного анализа рисков, преодолевает недостатки анализа чувствительности и анализа сценариев. Оба этих метода показывают воздействие определенного изменения в величине одной или нескольких переменных на показатель эффективности проекта (например, NPV). В отличие от анализа чувствительности и анализа сценариев, метод Монте-Карло позволяет: учитывать наличие корреляции между различными составляющими проекта; появляется возможность одновременно моделировать случайные изменения нескольких составляющих проекта с учетом условий коррелированности; сценарии являются случайными и формируются автоматически при реализации алгоритма метода Монте-Карло; сценарии формируются исходя из диапазонов возможных изменений случайных величин и подобранных законов распределения; количество случайных сценариев может быть сколь угодно велико, так как процесс имитации реализован в виде компьютерной программы, существует метод выбора необходимого числа сценариев, гарантирующего с определенной вероятностью надежность результатов моделирования.
Этапы проведения имитационного эксперимента представлены на рис.1
Рассмотрим технологию применения имитационного моделирования для анализа рисков инвестиционных проектов в среде ППП EXCEL.
В качестве примера продемонстрируем результаты проведения серии экспериментов с имитационной моделью инвестиционного проекта по выпуску синхронных гистерезисных двигателей (СГД), разрабатываемого ОАО «Армавирский электротехнический завод». ОАО «Армавирский электротехнический завод» входит в состав «ЭДС-Холдинг». Двигатели СГД используются в машинах по производству химических волокон. Использование данного двигателя позволит снизить не только накладные затраты, но и снизить переменные затраты в части расхода электроэнергии за счет полного согласования режимов работы источника питания с электродвигателем, что в конечном счете приведет к увеличению конкурентоспособности продукции.
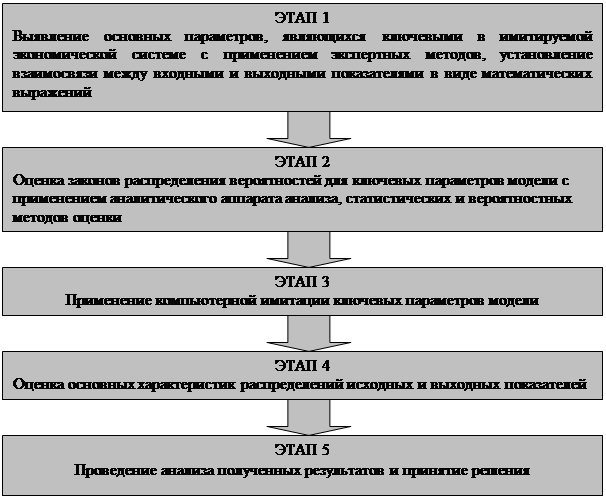
Рис. 1 Алгоритм методики проведения имитационного эксперимента оценки риска инвестиционного проекта
По имеющимся исходным данным в ходе исследования, были выделены рисковые факторы, влияющие на изменение значений денежных потоков и чистой приведенной стоимости проекта в целом (таблица 1).
Таблица 1
Риск-факторы инвестиционного проекта
|
Детерминированные факторы |
Стохастические факторы |
|
1. Постоянные затраты F |
1. Объем выпуска СГД Q |
|
2. Амортизационные отчисления A |
2. Цена за единицу продукции P |
|
3. Ставка процента по заемным средствам T |
3. Переменные затраты на единицу продукции V |
|
4. Ставка дисконтирования r |
|
|
5. Срок реализации проекта n |
|
|
6. Размер начальных инвестиций I0 |
|
В качестве концептуальной модели была взята модель оценки чистой современной стоимости проекта. Для ее оценки нам необходимо оценить чистый поток платежей, который поступает на предприятие в результате реализации продукции с учетом затрат, амортизации и налога на прибыль. Для расчета используется следующая формула:
NCFt = [Q * (P – V) – F – A] * (1 – T) + A,
Произведя дисконтирование потока платежей, и отняв значение начальных инвестиций, получаем чистую современную стоимость проекта:
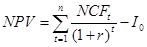 .
.
Группой экспертов, были оценены возможности изменений ключевых (исходных) переменных, определены вероятности р для различных сценариев реализации проекта, прочие параметры считаются постоянными величинами (таблица 2 и 3).
В качестве меры оценки риска рассмотрим: ожидаемый дисконтированный доход NPV, издержки неопределенности (ожидаемый чистый дисконтированный доход возможного выигрыша при решении отклонить проект или ожидаемый чистый дисконтированный возможный убыток при решении принять проект), нормированный ожидаемый убыток NEL=EL/(EI+EL), коэффициент вариации.
Экспертные оценки использовались только для определения диапазонов исходных показателей проекта, т. е. для определения их отклонения в ту или иную сторону. На практике же большинство экспертных процедур направлено на оценку результирующих показателей или конкретных факторов риска. Таким образом, сведен до минимума субъективный фактор, который мог бы повлиять на результаты решения.
Таблица 2
Вероятностные сценарии реализации проекта
|
Показатели |
Наихудший p=0,25 |
Вероятный p=0,5 |
Наилучший p=0,25 |
|
Объем выпуска Q, единиц |
6220 |
6720 |
7000 |
|
Цена за единицу P, долл. |
81,8 |
100 |
167,5 |
|
Переменные затраты на единицу V, долл. |
41,59 |
50,84 |
85,16 |
Проведение имитационных экспериментов в среде ППП EXCEL можно осуществить двумя способами – с помощью встроенных функций и путем использования инструмента «Генератор случайных чисел» дополнения «Анализ данных».
Таблица 3
Постоянные параметры проекта
|
Показатели |
Наиболее вероятное значение |
|
Постоянные затраты F, долл. |
100000 |
|
Амортизация A, долл. |
29033 |
|
Налог на прибыль T |
24 |
|
Норма дисконта r |
0,15 |
|
Срок проекта n |
6 |
|
Начальные инвестиции I0, долл. |
143000 |
Следует отметить, что применение встроенных функций целесообразно лишь в том случае, когда вероятности реализации всех значений случайной величины считаются одинаковыми. Будем также исходить из предположения о независимости ключевых переменных Q, V, P, а результирующий показатель NPV, исходя из центральной предельной теоремы, аппроксимируем с помощью нормального закона распределения. Тогда для имитации значений требуемой переменной можно воспользоваться математической функцией СЛУЧМЕЖДУ(). Как следует из названия, она позволяет получить случайное число из заданного интервала. При этом тип возвращаемого числа (вещественное или целое) зависит от типа заданных аргументов.
Рабочий лист с результатами, проведенного эксперимента представлен на рис. 2.
Величина ожидаемой NPV составляет 761962,146 долл., стандартное отклонение равно 522589,046. Можно сказать, что стандартное отклонение не превышает ожидаемого значения, но достаточно велико, что заставляет задуматься о рискованности проекта.
Результаты вероятностного анализа показывают, что шанс получить отрицательную величину NPV не превышает 7%. Общее число отрицательных значений NPV в выборке составляет 36 из 500.
Следовательно, с вероятностью около 92,8 % можно утверждать, что чистая приведенная стоимость проекта будет больше 0. Коэффициент вариации равен 0,69%, что говорит о достаточно высоком уровне риска проекта.
Несколько больший оптимизм внушают результаты анализа распределения чистых поступлений от проекта NCFt. Величина стандартного отклонения здесь составляет 58% от среднего значения.
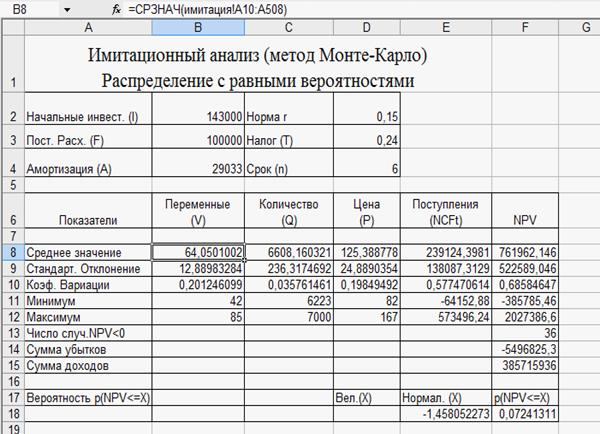
Рис 2. Результаты имитации с помощью встроенной функции СЛУЧМЕЖДУ
Сумма всех отрицательных значений NPV в полученной генеральной совокупности (-5496825,3) может быть интерпретирована как чистая стоимость неопределенности для инвестора в случае принятия проекта. Аналогично сумма всех положительных значений NPV (385715936) может трактоваться как чистая стоимость неопределенности для инвестора в случае отклонения проекта. Несмотря на всю условность этих показателей, в целом они представляют собой индикаторы целесообразности при проведении дальнейшего анализа. В данном случае они наглядно демонстрируют несоизмеримость суммы возможных убытков по отношению к общей сумме доходов (-5496825,3 и 385715939 соответственно).
Важнейшим этапом анализа является исследование зависимостей между ключевыми параметрами. Количественная оценка вариации напрямую зависит от степени корреляции между случайными величинами. На рис.3 и рис. 4 приведены графики распределения значений ключевых параметров V, Р и Q, построенные на основании 70 итераций.
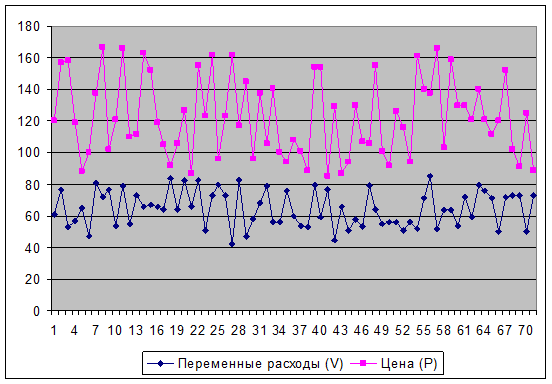
Рис. 3 Распределение значений параметров V и Р
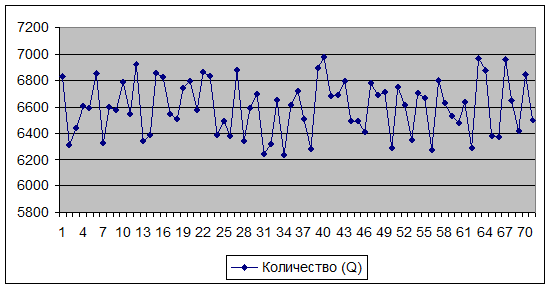
Рис. 4 Распределение значений параметра Q
Нетрудно заметить, что в целом, вариация значений всех трех параметров носит случайный характер, что подтверждает принятую ранее гипотезу об их независимости.
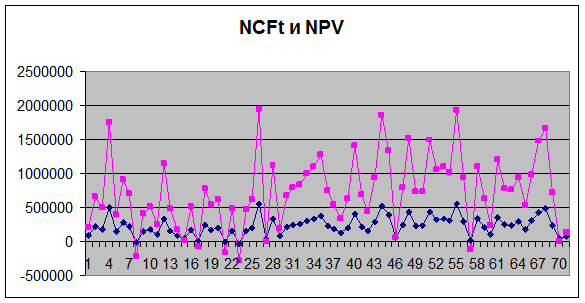
Для сравнения ниже приведен график распределения потока платежей NCF и величины NPV (рис. 5).
График наглядно демонстрирует, что направления колебаний NCF и NPV в точности совпадают и между этими величинами существует сильная корреляционная связь, близкая к функциональной.
Рис. 5 Зависимость между NCF и NPV
Результаты графического анализа подтверждаются с помощью инструмента «Корреляция» пакета «Анализ данных». Корреляционный анализ представлен в электронной таблице в виде квадратной матрицы (рис. 6).
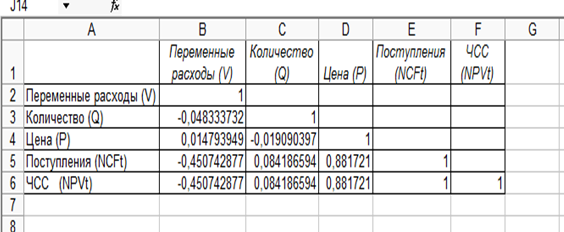
Рис. 6 Результаты корреляционного анализа
Как следует из результатов, выдвинутая гипотеза о независимости распределений ключевых параметров V, Q, Р в целом подтвердилась. Значения коэффициентов корреляции между переменными расходами V, количеством Q, и ценой Р (ячейки В3, В4, С4) достаточно близки к 0. В свою очередь величина показателя NPV напрямую зависит от величины потока платежей (r=1). Кроме того, существует корреляционная зависимость между Р и NPV (r=0,88). Как и следовало ожидать, между величинами V и NPV существует умеренная обратная корреляционная зависимость (r=-0,45).
Следует отметить, что близкие к нулевым значения коэффициента корреляции указывают на отсутствие линейной связи между переменными, но не исключают возможности нелинейной зависимости. Кроме того, высокая корреляция не обязательно всегда означает наличие причинной связи, так как две исследуемые переменные могут зависеть от значения третьей.
Подводя итог можно отметить, что в целом применение рассмотренной технологии проведения имитационных экспериментов в среде EXCEL трудоемкий процесс, ограничивающийся случаем равномерного распределения исследуемых переменных. Более удобным и эффективным способом оценки риска в среде EXCEL является использование специального инструмента анализа – «Генератор случайных чисел».
Этот инструмент предназначен для автоматической генерации множества данных заданного объема, элементы которого характеризуются определенным распределением вероятностей. Могут использоваться 7 типов распределений: равномерное, нормальное, Бернулли, Пуассона, биномиальное, модельное и дискретное. В данном случае будем исходить из предположения о нормальном распределении ключевых переменных. Число имитаций оставим равным 500. Рабочий лист с результатами эксперимента представлен на рис. 7.
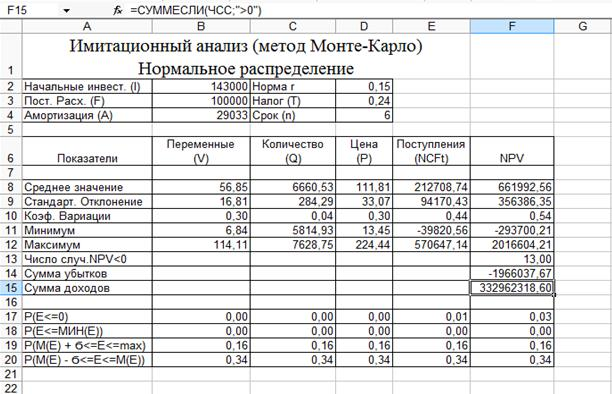
Рис. 7 Результаты имитации с помощью инструмента «Генератор случайных чисел»
Результаты проведенного эксперимента ненамного отличаются от предыдущих. Величина ожидаемой NPV равна 661992,56 при стандартном отклонении 356386,35.
Коэффициент вариации 0,54 несколько ниже, чем в предыдущем расчете. Результаты вероятностного анализа показывают, что шанс получить отрицательную величину NPV не превышает 3%. Общее число отрицательных значений NPV в выборке составляет 13 из 500. Таким образом, с вероятностью около 97% можно утверждать, что чистая современная стоимость проекта будет больше 0. При этом вероятность того, что величина NPV окажется больше чем М(NPV) + ϭ, равна 16%. Вероятность попадания значения NPV в интервал [M(NPV) – ϭ; M(NPV)] равна 34%.
При проведении имитационного эксперимента и последующего вероятностного анализа мы исходили из предположения о нормальном распределении исходных и выходных показателей. Справедливость сделанных допущений, по крайней мере, для выходного показателя NPV, нуждается в проверке. Воспользуемся инструментом «Описательная статистика», который автоматически вычисляет наиболее широко используемые в практическом анализе характеристики распределений. При этом определим значения сразу для всех переменных (V, Q, NCF, NPV). Результаты представлены на рис. 8.
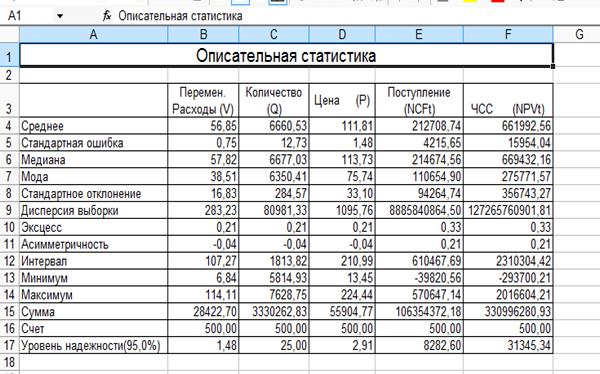
Рис.8 Описательная статистика
Медиана, являясь одной из характеристик центра распределения случайной величины, делит площадь под кривой распределения пополам. В симметричных распределениях она равна или близка по своему значению к математическому ожиданию. Как следует из полученных результатов, данное условие соблюдается для всех переменных (V, Q, P, NCF, NPV).
Эксцесс, характеризуя остроконечность (положительное значение) или пологость (отрицательное значение) распределения по сравнению с нормальной кривой, теоретически для нормального распределения должен быть равен 0. В данном случае положительный эксцесс наблюдается у распределений V, Q, P, NCF, NPV. Таким образом, их графики будут чуть остроконечнее, по сравнению с нормальной кривой.
Коэффициент асимметрии характеризует смещение распределения относительно математического ожидания. Для нормального распределения данный коэффициент равен 0. Малыми значениями на практике можно пренебречь. В частности асимметрию распределений V, Q, P можно считать несущественной. Распределения NCFt и NPV имеют небольшую правостороннюю асимметрию.
Осуществим оценку значимости коэффициента асимметрии для распределения NPV. Для этого рассчитаем стандартную ошибку по формуле:
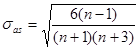 ,
,
где n – число значений случайной величины (500).
Если отношение коэффициента асимметрии s к величине ошибки ϭas меньше трех, то асимметрия считается несущественной, а ее наличие объясняется воздействием случайных факторов. В противном случае асимметрия значима и факт ее наличия требует дополнительной интерпретации.
ϭas = 0,11<3 – следовательно, асимметрию следует считать несущественной.
Аналогичным способом осуществим проверку значимости величины эксцесса – e. Формула для расчета стандартной ошибки эксцесса имеет вид:
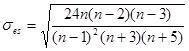 ;
;
ϭes = 1,48 <3 – эксцесс считается незначительным и его величиной можно пренебречь.
Графический анализ также не отвергают гипотезу о нормальности распределения NPV (см. рис.9).
Характеристика «Уровень надежности» показывает величину доверительного интервала для математического ожидания согласно заданному уровню надежности 95%. Для данного проекта это означает, что с вероятностью 95% величина математического ожидания NPV попадет в интервал (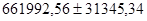 ).
).
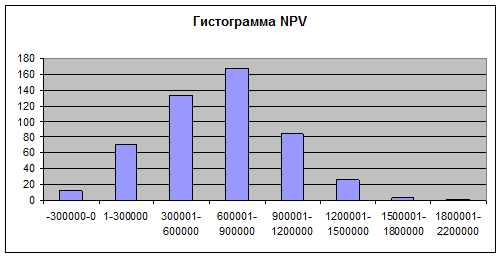
Рис. 9 Гистограмма распределения NPV
На основании результатов приведенного анализа, лицо, принимающее решение, должно оценить риск проекта и целесообразность его принятия. В данном случае, такие показатели, как нормированный ожидаемый убыток, коэффициент асимметрии распределения значений современной стоимости проекта говорят о рентабельности проекта. С другой стороны, такие показатели как коэффициент вариации, стандартное отклонение проекта говорят о нестабильности проекта, о высокой доле вариации и непредсказуемости результатов, а это влечет за собой высокий риск самого проекта. Для определенных исходных данных трудно принять однозначное решение. Большое значение при принятии решения имеет фактор готовности инвестора идти на риск, и в какой мере. Если инвестора не смущает такое большое значение коэффициента вариации, то он может принять этот проект. В любом случае, решение о принятии проекта всегда остается за инвестором.
В заключении, можно отметить следующее:
1. Имитационное моделирование является достаточно сложным инструментом, для анализа экономической деятельности и оценки рисков. Оно требует привлечения высококвалифицированных специалистов как со стороны экономистов, так и со стороны разработчиков ПО, реализующих имитационную модель. Именно это является одним из самых существенных ограничений в распространении этого инструмента оценки рисков.
Но именно этот инструмент является одним из самых точных и достоверных при анализе бизнес-процесса (при условии адекватности имитируемой модели), поскольку позволяет максимально приблизиться к реальным условиям функционирования экономической системы.
3. Большую роль при применении имитационного моделирования играет предварительный статистический анализ факторов модели и статистический анализ результатов. Статистический анализ может быть реализован в самой программной версии
модели, избавляя пользователя от дополнительных исследований, так и отдельно, оставляя решение этой задачи пользователю самостоятельно при помощи статистических пакетов.
Литература:
1. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов // 9-е изд., стер. – М.: Высш. шк., 2003. – 479 с.
2. Лукасевич И.Я. Анализ финансовых операций. Методы, модели, техника вычислений: учебное пособие для экономических вузов. – М.: ЮНИТИ, 1998. – 356 с.
3. Савчук, В. П. Анализ и разработка инвестиционного проекта: учебное пособие для экон. вузов // Киев: Абсолют-В: Эльга, 1999. – 230 с.