Анализ методов оценивания учащихся по физкультуре в школе

Особенностью предмета «Физическое воспитание», включающей в себя самые разнообразные спортивные дисциплины, является оценка достигнутых результатов учащегося. В учебном заведении множество видов спорта оценивается одной оценкой (в школе – отметками «5» или «4» или «3», в вузе – или оценками или отметкой о зачете). Причем результат ученика по каждому виду имеет, строго количественное значение (например, пробежал за 12,8 с, прыгнул на 140 см, подтянулся 24 раза). Другими словами, результат фиксируется в точной шкале высокого уровня (абсолютная шкала или шкала отношений), позволяющий объективно оценить место ученика, занятого в данном виде. Далее, по каждому виду определяется интервалы значений, количество, которых соответствуют принятой шкале оценок в учебном заведении и учащийся получает окончательную оценку по виду спорта. Такая оценка является качественной и относится к слабой шкале низкого уровня. Это так называемая ранговая шкала (другие ее названия: порядковая, предпочтения).

По существующей практике, в дальнейшем, находится усредненная оценка, которая и является окончательной. С точки зрения статистики усреднение качественных величин является некорректной, в смысле – не однозначной процедурой [1]. А не однозначность оценки  не повышает мотивацию учащихся к достижению более высоких результатов, ухудшает отношения в коллективе учебного заведения.

Проиллюстрируем оценки условных двух учеников для двух видов спорта (например, метания и прыжки) на схеме рисунка 1. Из примера видно, что оба ученика, имеющие сильно отличающиеся результаты, получают одинаковые оценки.

          УчI        УчII           УчI             УчII      

  2                      3                         4                        5                       

Рисунок 1. Схема отметок за результаты по двум видам спорта.

На рисунке штриховкой фигур показаны разные виды спорта. Заштрихованный (первый вид) оценка обоих учеников – 3; без штриховки (второй вид) – оценка обоих учеников – 4. Общая оценка обоих учеников по существующей практике оценивания – 4.

В школьной и студенческой жизни много различных увлекательных командных и личных состязаний не только в спорте, где победители выявляются по некоторому обобщенному (комплексному, свернутому) значению результата. Приведение многих разнообразных результатов к одному комплексному значению часто используется в практике оценивания самых разных объектов и деятельности. Обычно используют процедуру суммирования мест (с учетом или без учета значимости составляющих видов состязаний) и ранжирование, т.е. расстановка по занятым местам, по наименьшей сумме мест.

 В спорте обобщенная оценка встречается наиболее часто: рейтинги спортсменов (кубки Мира и Европы), многоборья в одном спортивном виде и различные полиатлоны, такие, как современное пятиборье, легкоатлетические многоборья, зимние многоборья, школьные многоборья, многоборья ГТО и другие.

 Задачами нашей работы являлись:

·         анализ существующих методов обобщенной оценки;

·          поиск новых методов для использования в школах и вузах;

·          определение их надежности и достоверности;

·          разработка рекомендаций для применения этой оценки в школе, вузе в зависимости от поставленных целей и заданных условий.

 Целями обобщенного оценивания могут быть:

- определение итогового результата или рейтинга спортсмена по различным этапам и видам многоборья (рейтинга учащегося);

- определение мест спортсменов в многоборьях (у школьников и студентов оценки по физкультуре);

- формирование сборных команд для участия в различных лично-командных командных и состязаний в конкурсах, многоборьях (полиатлонах).

В большом спорте используются следующие методы получения обобщенного итогового результата по видам и в многоборье:  по наименьшей сумме мест по отдельным видам (редко); по очкам за место, присваиваемым по специальным таблицам, например, в соревнованиях Формулы 1, этапах Кубков Мира по различным летним и зимним видам спорта и т.п. [2]; по очкам за результат, присваиваемым по специальным таблицам, например, легкоатлетические многоборья (Таблицы Очков ИААФ) [2].

В дополнение к перечисленным методам нам кажется интересным, а для школьных состязаний и перспективным, распространить известные в системном анализе, квалиметрии и прикладной статистике методы обобщенной (комплексной) оценки [3].

По стандартизованным  результатам (показателям) – для индивидуальных оценок.

В этом случае стандартизация результатов по каждому виду осуществляется по формуле

                         Xст_i= (X_i – Xavg)*A / σ_x           (1),

где - Xст_i, X_iсоответственно стандартизованные и исходные i – тые результаты, σ_xстандартное отклонение данных X_i, А– коэффициент, i = 1,2,…n, n - величина выборки.

    А = 1, если рост значения, улучшает показатель (например, длина - метания, прыжки);     

    А = -1, если уменьшение его значения, улучшает показатель (например, время - бег).

    2. По относительным приведенным результатам (нормированным), характеризующим их уровни относительно некоторых базовых норм – для индивидуальных оценок. В качестве базы могут быть использованы нормативы различного уровня (от международных до школьных). Часто нормативы вообще отсутствуют. В этом случае лучше всего в качестве базы использовать среднее значение (хотя можно брать за базу и минимальное значение, и максимальное значение).

Обобщенный нормированный показатель может быть выражен двумя формами:

·         Аддитивный показатель -

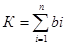
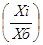
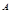                                                (2),

 где b_i– весовой коэффициент i-того показателя, Х_i – i-тый показатель, X_b – базовый показатель, А – показатель степени, i= 1,2,…n, n - величина выборки.

    А = 1, если рост значения, улучшает показатель (длина - метания, прыжки);     

    А = -1, если уменьшение его значения, улучшает показатель (время - бег)

·         Мультипликативный показатель - 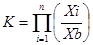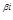, где β_i– весовой коэффициент.

 В рассматриваемой работе используется аддитивный обобщенный показатель с равными весовыми коэффициентами. Аддитивный показатель рекомендуется использовать в том случае, когда индивидуальные и базовые показатели мало отличаются друг от друга. При большом различии, например в оценке надежности технических систем, чаще применяется мультипликативный обобщенный показатель [4].                              

3. Многомерное  группирование  (формирование групп, кластеров) на основе некоторых статистических метрик [5]  – для групповых оценок и определения интервалов для свертки итоговой индивидуальной оценки по принятым шкалам (пятибалльная шкала, десятибалльная и др.).

Оценка по обобщенному показателю по относительным индивидуальным результатам актуальна при оценке состязательных результатов в многоборьях (чем являются уроки физкультуры и различные соревнования и конкурсы в школах), в тех случаях, когда отсутствуют специальные таблицы и нормативы.

 Использование многомерных группировок актуально при формировании сборных команд классов, школы в различных состязаниях. Кроме того в любых статистических исследованиях группировка первичных данных является основным приемом дальнейшей работы с собранной информацией.
       Анализ методов обобщенной оценки проводился в два этапа. На первом этапе определялась достоверность рассматриваемых методов.  За критерий достоверности обобщенной оценки выбрана наиболее распространенная в мировом спорте оценка по очкам за результат. Использовались и  нормативы Российской Единой Спортивной Классификации (ЕВСК) согласованной с международной системой ИААФ [6].

В качестве модельного примера многоборья принято женское легкоатлетическое семиборье. Для этого вида спорта имеются очки таблицы ИААФ, разрядные нормативы ЕВСК, выраженные в значениях натуральных величин и очках, что обеспечивает возможность оценить индивидуальный результат в многоборье, используя различные методы оценки.   Условные результаты легкоатлетического семиборья девушек приведены в таблице 1.

На втором этапе сравнивались результаты девушек 9-х классов по физкультуре по трем разным видам (прыжки в длину с места, бег 2000 м и упражнения на развитие мышц брюшного пресса).                     

   Таблица 1. Модельные условные итоговые результаты легкоатлетического семиборья                   

В таблице 2 приведены очки за результаты, приведенные в таблице 1, суммарный результат за семиборье в очках ЕВСК и место, занятое спортсменкой.

Таблица 2. Результаты табл.1, переведенные в очки ЕВСК

 

Аналогичные таблицы были построены:

·         По наименьшей сумме мест за каждый вид

·         По относительным результатам, приведенным ко II-му юношескому разряду

·         По относительным результатам, приведенным к среднему результату по каждому виду

·         По стандартизованным данным по каждому виду.

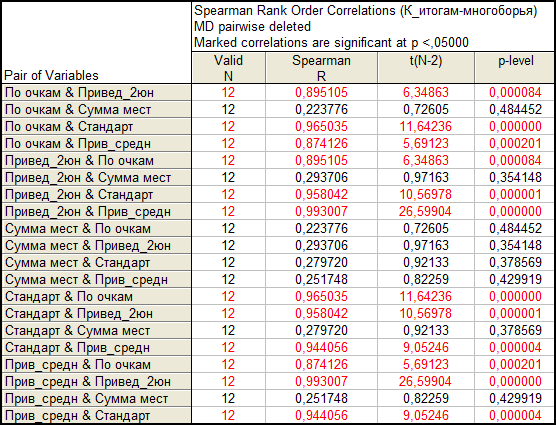
Сводные результаты различных методов в определении мест приведены в табл.3. Результаты оценивались с помощью парных ранговых коэффициентов корреляции Спирмена. Оценка производилась в среде Statistica 6 в модуле «Непараметрические данные». Коэффициенты ранговой корреляции Rи их значимость приведены в табл. 4.

Таблица 3.  Сводные  результаты занятых мест в семиборье

 

 Данные таблицы позволяют сделать заключение о большой степени сходства оценок, полученных по таблицам ЕВСК и различным относительным результатам.

Таблица 4. Коэффициенты парной ранговой корреляции Спирмена их значимость

 Во второй части работы, используя рекомендации  анализа методов, решались следующие задачи

·         Определение отметки каждого учащегося по троеборью;

·         Определение места каждого учащегося в приведенном троеборье.

 

В таблице 5 приведены результаты девушек 9-х классов МОУ «Воткинский лицей» в 2008 г.

Задача определения отметки каждого учащегося решается просто только для каждого вида упражнения, если существуют нормативы. Такие, например, как нормы, приведенные в таблице 6. В таб.6 приведен фрагмент нормативов для школ, работающих по существующей пятибалльной системе. Аналогичные нормативы существуют для школ, работающих по десятибалльной системе [7]

 

Таблица 5. Спортивные результаты девушек 9-х классов школы по трем видам упражнений (2008 год)

 

Код     прыжок    бег 2000м          пресс        Код      прыжок     бег 2000м    пресс

ученика длина, см      с              кол-во       ученика   длина, см             с       кол во

а01             170               622            23

а02             165               600            12

а03             190               593            20

а04             150               662            12

а05             200               593            20

а06             185               600            22

а07             150               581               18

а08             205               622            23

а09             180               625            20

а10             170               694            20

а11             185               602            18

а12             200               625            21

а13             205               548            20

а14             175               683            16

б01             170               625            17

б02             165               611            20

б03             180               648            20

б04             170               600            19

б05             170               604            14

б06             170               611            20

б07             190               653            17

б08             165               690            18

б09             170               583               19

б10             200               621            19

б11             150               545            18

б12             180               9,23           16

б13             205               645            15

б14             165               579             20

в01             180       653              27

в02             175       631              15

в03             155               632      15

в04             165               635      15

в05             180               645      25

в06             150               623      16

в07              170              635      15

в08              165              635      15

в09              155              623      16

в10              185              625      16

в11              180              654      26

в12              175              605      24

в13              165              645      25

в14              155              643         16

г01              190              636      13

г02              165              590      12

г03              165              593      13

г04              175              659         18

г05              180          587         18

г06              180               604         15

г07              185               659     24

г08              165              630      12

г09              190               625     20

г10              150              629      12

г11              190              626       21

г12              170              659      15

г13              185              658         16

г14              155              660         15

 

Таблица 6. Фрагмент нормативов по физкультуре для старших школьников

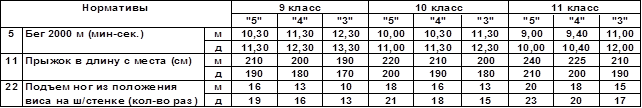
Проводилось сравнение итоговых результатов по четырем ранее рассматриваемых методов:

1.      Оценка по обобщенному относительному показателю, на индивидуальных показателей, приведенных по каждому виду к нормативу оценки «4»;

2.      Оценка по баллу, полученному за каждый результат по таблице 6 и сведенный в единую оценку (округленное среднее);

3.      Оценка по обобщенному показателю вектора стандартизованных индивидуальных результатов;

4.      Оценка по обобщенному показателю вектора индивидуальных результатов, нормированных по среднему

В таблице 7 приведена матрица парных линейных коэффициентов корреляции, после проверки нормальности итоговых результатов, гистограммы которых показаны на рисунке 2.

Таблица 7. Корреляционная матрица обобщенных результатов троеборья

 

 

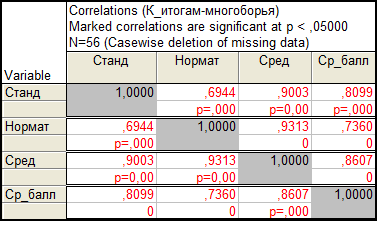
Визуальная оценка нормальности распределения позволяет считать, что распределение в целом подчиняется нормальному закону. Гистограммы качественно показывают, различие в соотношении итоговых результатов относительно среднего и, следовательно, неоднородность в распределении мест и отметок в разных методах оценки.

 

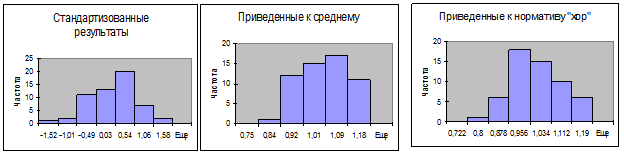
Рис. 2. Гистограммы обобщенных итоговых результатов троеборья

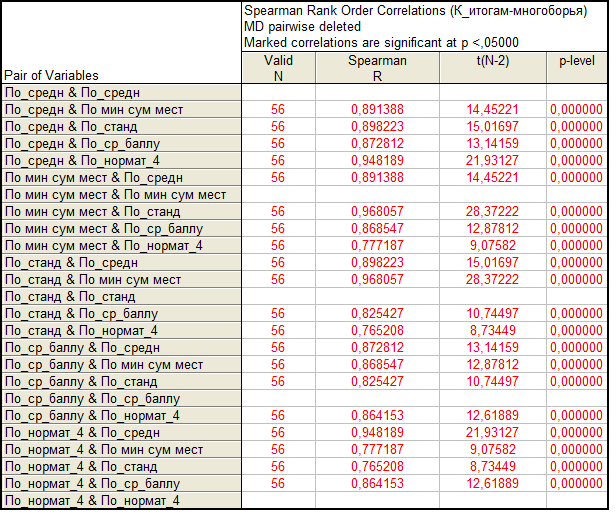
В таблице 8 приведены значения парных ранговых коэффициентов Спирмена и параметры, характеризующие их значимость. Как было показано ранее, для определения мест наиболее близким к общепринятому классическому методу является обобщенная оценка стандартизованных результатов. При определении мест в троеборье неожиданно оказалась близость минимальной суммы мест к итогам стандартизованных результатов. Этот противоречивый результат (таблица 4) возможно случаен, возможно, объясняется малым количеством видов, возможно, какими-то другими обстоятельствами, которые необходимо далее исследовать. Тем не менее, стабильно близкими являются стандартизованные итоговые результаты и результаты, нормированные по среднему.

Таблица 8. Коэффициенты парной ранговой корреляции Спирмена и их значимость

Определение отметок учащихся производилось после выделения четырех групп («отличников», «хорошистов», «троечников» и группа учащихся со слабым физическим развитием). Для этого применялся упрощенный кластерный анализ - метод «К – среднего» [8]. Число групп, на которое равномерно разбивается размах, определяется по формуле

                      N = K - 2                           (3),

где, N – число групп, K - число баллов в принятой шкале. Остальное понятно из рисунка 4.      

Отметки учеников по спортивным результатам, приведенным в таблице 6, показаны в таблице 9.

Таблица 9. Отметки учащихся по обобщенным результатам разными методами     

Уч     Станд     Норм  По сред

а01         4        4           5

а02            3      2           2

а03            4      4           5

а04            2      2           2

а05            5      4           5

а06            4      4           5

а07            3      3           3

а08            5      4           5

а09            4      4           4

а10            4      4           4

а11            4      3           4

а12            4      4           5

а13            5      4           5

а14            2      3           3

б01            3        3         3

б02            4      4           4

б03            3      4           4

б04            4      3           4

б05            3      2           3

б06            4      4           4

б07            3      3           4

б08            3      3           3

б09            4      3           4

б10            4      3           4

б11            4      3           4

б12            4      3           4

б13            4      2           3

б14            4      4           4

 

Уч       Станд    Норм  По сред

в01           4       5           5

в02           3       2           3

в03           2         2         2

в04           3       2           3

в05           4       5           5

в06           2       3           3

в07           3       2           3

в08           3       2           3

в09           3       3           3

в10           3       3           3

в11           4       5           5

в12           4       5           5

в13           4       5           5

в14           2       3           3

г01           3       2           3

г02           4         2         3

г03           3       2           3

г04           3       3           3

г05           4       3           4

г06           3       2           3

г07           4       5           5

г08           3       2           2

г09           4       4           4

г10           2       2           2

г11           4       4           5

г12           2       2           3

г13           3       3           3

г14           2       2           2

В таблице 10 приведены сводные данные итогов мест, занятыми ученицами в троеборье, определенные разными методами.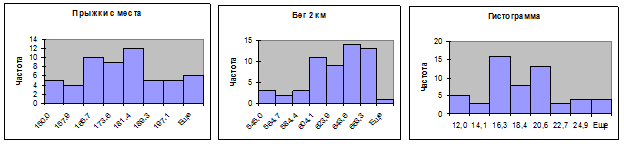

Рисунок 3. Распределение результатов учеников по видам упражнений

 Таблица 10.

По стандартизованным данным			По нормативу "4"	По среднему
Абсолютная успеваемость		85,71%	71,43%	89,29%
Уровень качества		51,79%	37,50%	50,00%

 

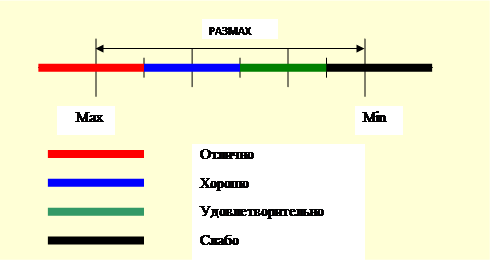
Рисунок 4. К определению отметок за многоборье методом «К-средних»

Если веса каждого вида равны, обобщенный нормированный показатель (2) приобретает вид:

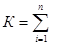
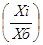
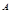                                             (4),

 где Х_i – i-тый показатель, X_b – базовый показатель, А – показатель степени (1, -1), i= 1,2,…n, n - величина выборки.

Для стандартизованных результатов каждого вида, если результаты нормальны обобщенный показатель имеет вид                                                                           

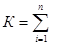
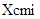                                            (5).

В этом случае стандартизация результатов по каждому виду Xcmi осуществляется по выражению (1) с равными весовыми коэффициентами.

Для результатов по видам, нормальность которых не очевидна, целесообразно использовать обобщенный показатель (4).

Расстановка обобщенных результатов по приоритетам (по убыванию) позволяет установить ранг (место) каждого учащегося в рассматриваемом троеборье. Особенностью ранжирования по нормативам и среднему баллу является большое количество сопряженных рангов.

Учитывая, что вид распределения по видам (рисунок 3) нельзя считать нормальным, рекомендовать использовать обобщенный показатель с использованием стандартизованных данных следует осторожно. Следует отказаться и от среднего балла, как некорректной величины. Можно предположить, что обобщенный показатель, нормированный по среднему, является предпочтительным

 

                                               

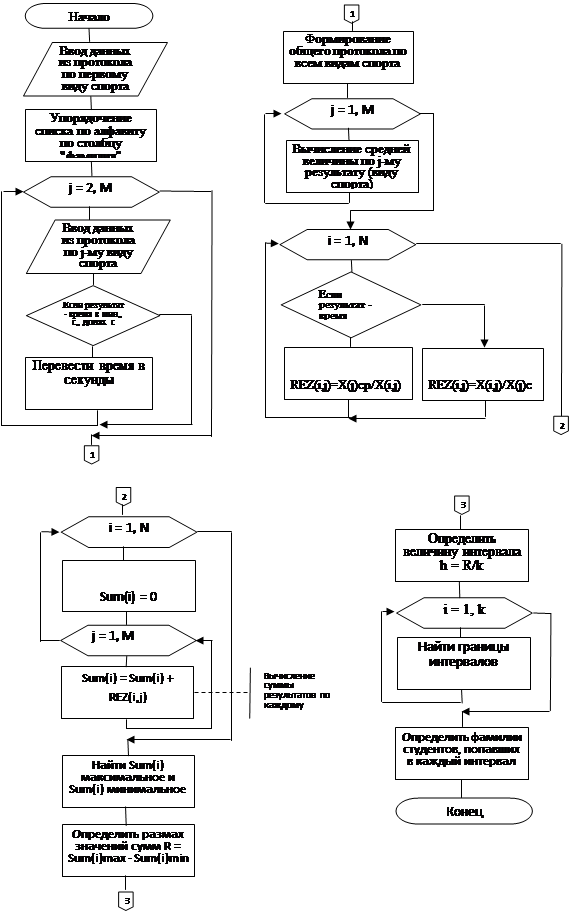
Рис.5  Блок-схема алгоритма определения итогов по среднему результату

При подведении итогов требуется выполнить ряд вычислительных процедур, что может осложнить использование полученных результатов неподготовленным персоналом. Однако, умение пользоваться Excel, его вложенными функциями и процедурами не вызовет сложностей.  Кажущаяся сложность вычислительных процедур при подведении итогов соревнований легко может быть устранена при помощи автоматизации, например, использованием макросов в Microsoft Office Excel или использованием специальных программ. Пример блок-схемы алгоритма расчета обобщенных результатов, применяя наиболее простой индивидуальный показатель, нормированный по среднему значению приведен на рис.5

Выводы по работе.

1.      Впервые в практике подведения итогов в спортивных многоборьях предложены методы оценки, использующие относительные безразмерные показатели достижений по каждому виду многоборья.

2.      Сильная связь метода обобщенной оценки спортивных результатов, отнесенных к некоторой норме или к среднему, в сравнении с классической оценкой по таблицам очков (коэффициент ранговой корреляции R = 0,87 - 0,89 при его значимости 0,0002 - 0,00008) дают основания для рекомендации использования предложенного метода для оценивания достижений школьников по физкультуре, как наиболее простого.

3.      В качестве нормативной базы могут быть использованы разрядные нормативы, нормативы, установленные органами здравоохранения и образования или нормативы, установленные для соответствующих возрастов, адекватно отражающие физическое развитие школьника. При отсутствии нормативов за базу можно рекомендовать среднее значение по каждому виду.

4.      Показано, что метод оценки многоборья по минимальной сумме мест не стабилен и имеет низкую надежность.

 

Литература:

1.    Новиков Д.А. Статистические методы в педагогических исследованиях. М.: МЗ – Пресс, 2004. с. 11 – 26

2.    grandrussian.ru/…/24-semibore-i-desyatibore.html)

3.    Ногин В.Д. Принятие решений в многокритериальной среде: количественный подход М.: Физматлит, 2002. – 176 с.

4.    Гличев А.В. Научная система управления качеством продукции – В кн: -Надежность и долговечность машин и оборудования. – М.: Изд. стандартов, 1972. – 315 с.

5.    Ким Дж. О., Ч.у. Миллер и др. Факторный, дискриминантный и кластерный анализ. – М.: Финансы и статистика, 1989                              .

6.    Ушакова Н.А. Принципы расчета разрядных норм ЕВСК в легкоатлетическом семиборье. www.scamper.ru/stati/4401/           

7.     www.zloy-fizruk.narod.ru   

8.    Статистика: Курс лекций /Харченко Л.П. и др.;- Новосибирск: Изд-во НГАЭУ, 1996. -310 с..