Использование асимметричных мер риска при формировании оптимального портфеля ценных бумаг

Проблемы формирования портфеля ценных бумаг и его оценки занимают одно из ведущих мест в современной экономической теории и практике, что обусловлено их актуальностью в условиях развитого рынка.

Для того чтобы сформировать оптимальный портфель ценных бумаг необходимо разработать инвестиционную стратегию, которая основывается на анализе доходности от вложения, времени инвестирования и анализе возникающих при этом рисков. Главная цель формирования портфеля состоит в стремлении получить требуемый уровень ожидаемой доходности при более низком уровне ожидаемого риска.

Все участники фондового рынка действуют в условиях неопределенности. Исход практически любых операций купли-продажи ценных бумаг не может быть точно предсказан, то есть сделки подвержены риску.

Инвестиционный риск представляет собой вероятность возникновения финансовых потерь в виде снижения капитала или утраты дохода, прибыли вследствие неопределенности условий инвестиционной деятельности. Доходность и риск являются взаимосвязанными категориями. Наиболее общими закономерностями, отражающими взаимную связь между принимаемым риском и ожидаемой доходностью деятельности инвестора, являются следующие:

- более рискованным вложениям, как правило, присуща более высокая доходность;

- при росте дохода уменьшается вероятность его получения, в то время как определенный минимально гарантированный доход может быть получен практически без риска.

Принцип формирования портфеля ценных бумаг, при котором снижение риска достигается за счет включения в портфель большого числа различных акций, называется диверсификацией. Основоположником данной теории считается Гарри Марковиц.

Согласно теории Г. Марковица, при обосновании портфеля инвестор должен руководствоваться ожидаемой доходностью и стандартным отклонением. Ожидаемая доходность рассматривается как мера потенциального вознаграждения, связанная с конкретным портфелем, а стандартное отклонение — как мера риска, связанная с данным портфелем. При этом делается важное предположение: инвестор при всех прочих условиях предпочтет высокую доходность, если будут заданы два портфеля с одинаковыми стандартными отклонениями. Если же инвестору предстоит выбор между портфелями, имеющими одинаковый уровень ожидаемой доходности, то предпочтение отдается портфелю с минимальным риском, то есть, по сути, получению большего дохода при минимуме возможного отклонения. [1].

Другой мерой финансового риска является ожидаемая полезность. Полезность выражает меру удовлетворения, которое получает субъект от потребления блага. Впервые понятие «полезность» ввел в науку швейцарский математик Даниэль Бернулли в 1738 г.

Основополагающим объектом теории полезности является функция полезности u=u(x), определяющая полезность денежной суммы размера x для ЛПР (Лица, Принимающего Решение). Такая функция u(x) должна быть монотонно неубывающей, определенной на множестве R+=[0; ∞). Функция полезности - оценка восприятия полезности той или иной финансовой прибыли (или потери).

Однако теория ожидаемой полезности не всегда объясняет поведение людей в условиях неопределённости. Возникают парадоксы поведения, которые можно объяснить, введя понятие  «асимметрия».

Асимметрия - это различие в склонности к риску в случае прибылей и убытков. Это различие было подробно описано в теории перспектив (теории проспектов), авторами которой являются Дэниэл Канеман и Амос Тверски. Проспекты понимаются как альтернативы выбора с неопределёнными денежными исходами,  включающие в себя не только распределение выигрышей, но и способ описания или постановки вопроса.

Теория проспектов относится к области экономической психологии, которая в последние десятилетия заметно упрочила свои позиции и стала с точки зрения экономического сообщества вполне респектабельной наукой. Сотни научных публикаций появляются в таких известных международных изданиях, как American Psychologist, Journal of Economic Psychology, The American Economic Review и др. Среди публикаций на русском языке можно выделить коллективный труд «Проблемы экономической психологии» [2], а также переведенный с английского сборник «Принятие решений в неопределенности: правила и предубеждения», в котором приведены работы Д. Канемана, А. Словика, А. Тверски.[3].

Дэниэл Канеман, профессор Принстона и первый психолог, получивший Нобелевскую премию по экономике за исследования, проводимые им совместно с Амосом Тверски, отчасти объяснял тягу к определенным действиям на рынке присущей инвесторам «иллюзией контроля». Эту иллюзию он называл «теория проспектов». Теория проспектов, предложенная Д. Канеманом и А. Тверски в 1979 году, описывает поведение людей, когда они принимают решения в условиях риска. Канеман изучил интеллектуальную составляющую процесса инвестирования — каким образом трейдеры оценивают свои шансы и рассчитывают уровень риска, — чтобы узнать, как часто люди  действуют, исходя из ошибочной уверенности, что они знают больше, чем на самом деле. Канеман и Тверски обнаружили, что обычно человек действует в соответствии с правилом, которое они окрестили «законом малых чисел», то есть делает выводы на основании небольшого объема данных.

Основные положения теории проспектов:

Во-первых, в результате экспериментов было установлено, что люди придают большее значение потерям, чем приобретениям, даже если их величина одинакова. Другими словами, потери всегда кажутся «большими», чем приобретения. В частности, отношение к потерям проявляется в так называемом эффекте собственности (или вклада), согласно которому потеря какого-либо предмета ощущается людьми сильнее, чем его приобретение.

Во-вторых, авторы теории проспектов установили, что отношение людей к риску сильно зависит от формулировки задачи выбора. Эта особенность человеческого поведения тесно связана с отношением к потерям и также не учитывается в теории ожидаемой полезности. Она заключается в том, что люди обычно уклоняются от риска, чтобы получить гарантированный выигрыш, и предпочитают риск, чтобы избежать гарантированных потерь.

Результаты исследований подтверждают общий вывод теории проспектов о том, что формулировка задачи влияет на предпочтения людей и их отношение к риску. Если задача выбора представлена «в терминах приобретений», то люди уклоняются от риска. И наоборот, если задача выбора представлена «в терминах потерь», то люди предпочитают рисковать. Это психологическое явление получило название эффект обрамления (framing).

«Эффект обрамления» помогает лучше понять поведение людей в ситуациях риска. Однако он имеет не только теоретическое значение, но может быть использован и в практических целях. Например, с его помощью можно предсказывать поведение людей при принятии решений в зависимости от того, как сформулирована задача выбора — в терминах выигрышей или в терминах проигрышей. Если задача представлена в терминах выигрышей, то в большинстве случаев люди будут склоняться к избеганию риска. Если же задача представлена в терминах проигрышей, то, скорее всего, будет наблюдаться обратная тенденция — стремление к риску. Более того, можно не только предсказывать поведение людей, но и влиять на него, изменяя тип обрамления в зависимости от того, какое решение необходимо инициировать — осторожное или рискованное.

В-третьих, еще одно отличие теории проспектов от теории ожидаемой полезности заключается в отношении людей к вероятности получения того или иного результата. Было установлено, что люди склонны завышать маленькие вероятности и занижать средние и большие вероятности достижения значимых для себя результатов. Это явление называют эффектом субъективной оценки малых, средних и больших вероятностей. [4].

Рассмотрим применение теории проспектов к оценке риска, т.е. при известных физических вероятностях. В теории проспектов предпочтение среди функций-решений определяется критерием вида:

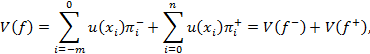
где величины π – некоторые веса. Таким образом, проспект разбивается на положительную и отрицательную части, представляющие соответственно приобретения и убытки.

Веса в теории проспектов представляют собой «искажённые» вероятности, причём на искажение влияет не абсолютное значение результата, а только ранг (порядок) результата среди всех результатов проспекта.

Теория проспектов была применена не только для объяснения данных экспериментов, полученных в лабораторных условиях, но и в исследованиях реального экономического поведения. В том числе может применяться при формировании портфелей ценных бумаг. Для использования асимметричных мер риска доходностей ценных бумаг и их портфелей следует использовать показатели доходности, множество значений которых симметрично относительно 0, причем 0 соответствует случаю неизменности цены акции.

Следствием возникновения теории проспектов стала предложенная Канеманом и Тверски S-образная функция полезности, которая базируется на следующих положениях теории:

а) Зависимость от исходного положения (reference dependence) — то есть данная функция оценки определена в координатах «выигрыши» и «убытки», ценность которых, в свою очередь, определяется относительно референтной, исходной точки. Альтернативы оцениваются индивидами не в терминах категорий общего, совокупного благосостояния, а посредством изменений в благосостоянии относительно так называемого положения статус кво, начального положения.

б) Уклонение от потерь (loss aversion) — другими словами, функция является более крутой в случае убытков (отрицательная область определения), чем в случае выигрышей (положительная область определения). Обычно, в большинстве случаев, вогнутая для выигрышей и выпуклая для потерь.

в) Уменьшающаяся чувствительность (diminishing sensitivity) — то есть предельная ценность как выигрышей, так и потерь уменьшается с увеличением их размера.

На рис. 1 приведена форма функции полезности денег, которая соответствует отношению к риску, выявленному в результате экспериментов Канемана и Тверски. Эта функция более «крута» в области потерь по отношению к некоторой точке отсчета, взятой за ноль на рисунке. Та­кая форма функции соответствует так называемым «эффекту отраже­ния»  и «неприятию потерь».

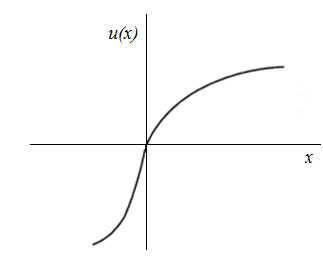
Рис.1. S-образная функция полезности денег

Как отмечал Бернулли, люди становятся все более безраз­личными к получению еще одного рубля по мере того, как заходит речь о получении все больших сумм. Аналогично по мере того, как речь за­ходит о все больших потерях, люди становятся все более безразличны к потере одного рубля, т.е. происходит такое же «насыщение». Этот эф­фект и называют «эффектом отражения».  «Неприятие потерь» — эффект, состоящий в том, что люди более чувствительны к потерям, чем к приобретениям. Ему соответствует более крутая форма функции в области отрицательных значений (по­терь). [5].

Гладкая  функция полезности f(t) применима как к прибылям, так и к ущербу. Она обладает следующими свойствами: f(0) = 0, функция f(t) возрастающая вогнутая при  t ≥ 0 и выпуклая при t ≤ 0. Кроме того полагаем, что эта функция нормированная: f′(0) = 1. Эта функция применима к оценке риска, при этом риск соответствует функции -f(t) (рост полезности означает уменьшение риска). Если функция распределения случайной величины – будущей доходности Х равна F_X(x), то в качестве асимметричной меры риска принимаем:

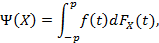
где (-p,p) – множество значений показателя доходности.

В ходе исследования были рассмотрены следующие S-образные функции полезности:

1)   Квадратичная функция полезности:

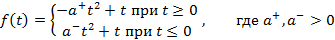
Соответствующая ей мера риска имеет вид:

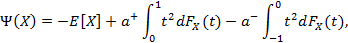
где E  – математическое ожидание.

2)   Кубическая функция полезности:

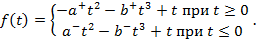
3)   Экспоненциальная функция

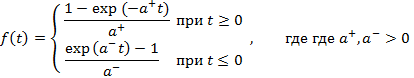
Данный подход применялся к оценке риска при формировании портфеля ценных бумаг. Экспериментально было выявлено, что применение мер риска, основанных на асимметричных функциях полезности, приводит к более эффективному формированию портфелей ценных бумаг.

Литература:

1.    Бочаров В.В., Швандар В.А. Инвестиционный анализ. – М.: «Юнити», 2000.

2.    Журавлев А.Л., Купрейченко А.Б., Позняков В.П. Проблемы экономической психологии. – М.: Изд-во Института психологии РАН., 2004.

3.    Канеман Д., Словик А., Тверски А. Принятие решений в неопределенности: правила и предубеждения. – М.: Изд-во Института прикладной психологии «Гуманитарный центр», 2005.

4.    Плаус С. Психология оценки и принятия решений / Перевод с англ. — М.: Информационно-издательский дом «Филинъ», 1998.

5.    Шоломицкий А. Г. Теория риска. Выбор при неопределённости и моделирование риска. – М.: Изд-во ГУ ВШЭ, 2000