Основные предположения
- Данная модель строится на предположениях Пенни-Тейлора (Область действия взрыва считается несжимаемой, использован принцип геометрического подобия).
- Выделившая энергия концентрируется в одной точке – центре заложения ВВ (точечный взрыв).
При моделировании расчетной схемы разрушения горной породы при взрыве сферического заряда рассматривается случай, когда начальная энергия взрыва сконцентрирована в одной точке, а точнее в центре полости заложения ВВ. В развитии такого процесса взрыва выделяют две стадии [3, с. 61].
На первой полость взрыва движется по траектории, определяемой линейной функцией. На второй стадии, когда полость взрыва достигает радиуса полости заложения снаряда, происходит изменение в движении границ (Уравнения движения будут рассмотрены ниже). В этом случае выделяются две зоны: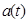 
- радиус полости взрыва, 
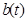- положение фронта дробления.
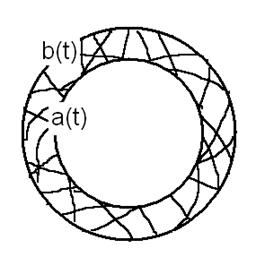
Рис. 1. Зонная модель разрушение горных пород при точечном взрыве.
В зоне взрыва движение описывается камуфлетным уравнением Пенни [3, с. 65-69]:
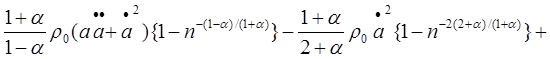
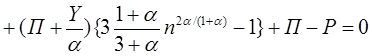(1)
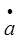- скорость изменения радиуса полости взрыва.
Предполагается, что влияние изменения плотности среды в уравнении (1) мало и плотность равна начальной. Из условия несжимаемости в зоне дробления имеем соотношение [1]:
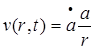, (2)
Считается, что в зоне сдвигового дробления при расширении полости взрыва компоненты тензора напряжений удовлетворяют условию пластичности Кулона-Мура 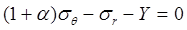[3]:
, (3)
где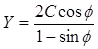 
, 
.
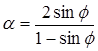Здесь С – коэффициент сцепления,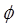 
- угол трения.
На границе полости взрыва радиальное напряжение определяется давлением газов в полости [4]:
,
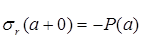где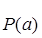 
- давление на границе полости взрыва, определяется следующим уравнением [3]:
 |
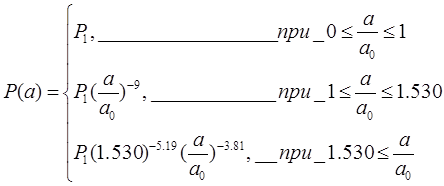(4)
Построение решения и моделирование
Для удобства приведем уравнение Пенни (1) к безразмерному виду, вводя переменные по времени и расстоянию:
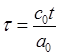
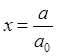(5)
Тогда основное уравнение сводится к следующему виду:
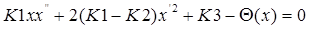
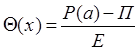(6)
Будет легче построить решение уравнение Пенни, если ввести новые переменные следующим образом:
 |
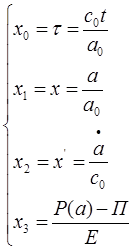(7)
Подставляя в уравнение Пенни переменные, представленные выше, получим следующую систему дифференциальных уравнений первого порядка:
 |
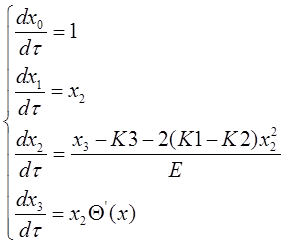(8)
Методика расчетов
Как говорилось выше, на первой стадии, когда радиус взрыва меньше радиуса полости заложения снаряда, расширение полости взрыва происходит по линейной зависимости.
 |
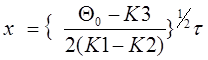(9)
 |
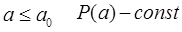Данная зависимость определена с учетом того, что при
Если конечный момент времени первой стадии выбрать как начальный второй стадии, то решение системы (8) определяем при следующих начальных условиях:
 |
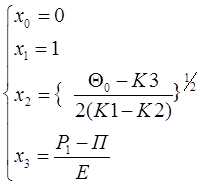Давление на границе полости взрыва находим по соотношению (4).
Результаты моделирования
Описанная выше схема реализована для расчета параметров взрыва. Разработана программа в среде C++ с интерфейсом ввода начальных условий и возможностью корректировки вычислительной сетки.
Результаты моделирования точечного взрыва в грунте составлены при следующих начальных параметрах:
- Глубина заложения ВВ – 15.24 м.
- Начальный радиус камуфлетной полости – 2.54 см.
- Начальная плотность породы – 1416 кг/м3.
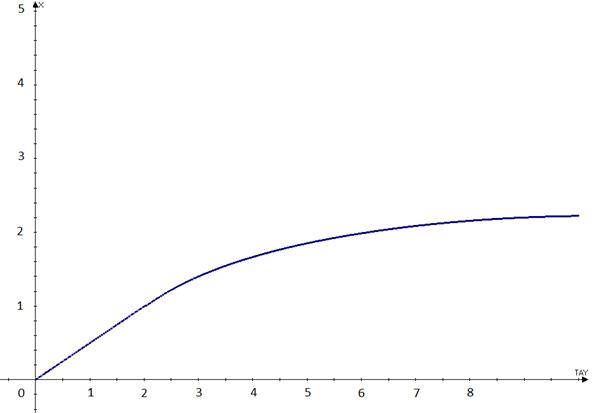
Рис. 3. Закон изменения относительного радиуса полости взрыва , (график представлен в безразмерных величинах).
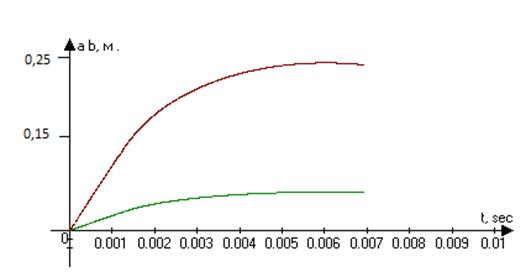
Рис. 4. Изменение радиуса камуфлетной полости взрыва и области дробления породы.
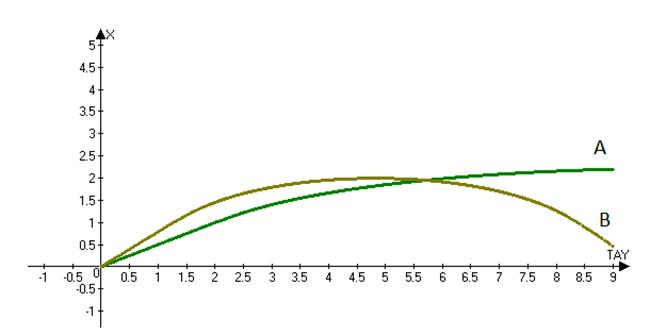
Рис. 5. Зависимости изменения относительного радиуса взрыва от глубины заложения ВВ, (график представлен в безразмерных величинах, А=15 м., В=100 м.).
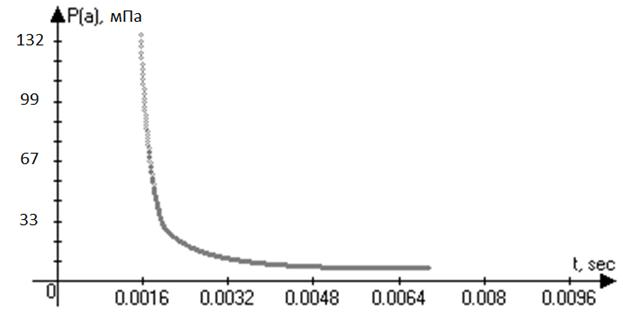
Рис. 5. Изменение давления на границе взрывной области.
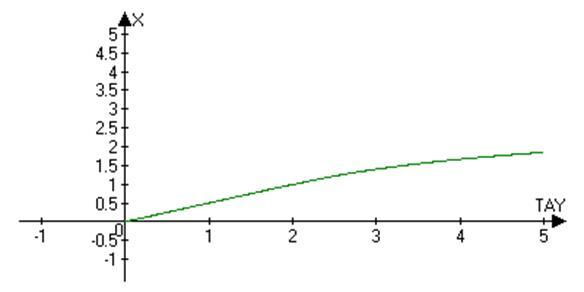
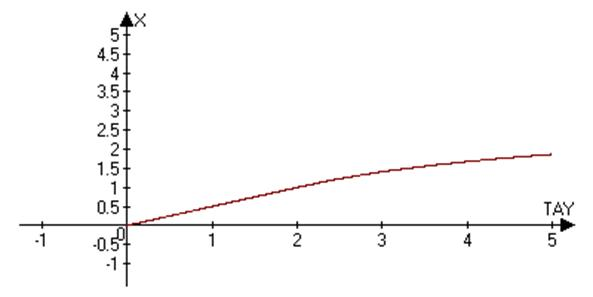
Рис. 6-7. Сравнение результатов моделирования системы при различных сетках дифференцирования (tay=0.01 и 0.001 соответственно).
Библиографический список:
- Бондарик, Г. К. Текстура и деформация глинистых пород / Г. К. Бондарик, А. М. Царева, В. В. Пономарев. – М.: Недра, 1975. – 168 с.
- Ляшенко, П. А. Модель деформации микроструктуры грунта / П. А. Ляшенко // Научный журнал КубГАУ [Электронный ресурс]. – Краснодар : КубГАУ, 2005. – №03(11). – Режим доступа: http://ej.kubagro.ru/2005/03/02/p02.asp.
- Чедвик, П. Механика глубинных подземных взрывов / П. Чедвик. – М. : Мир, 1995. – 48 с.
- Кузнецов, В. М. Математические модели взрывного дела. / В. М. Кузнецов. – Новосибирск.
