В настоящее время комбинированные программно-аппаратные системы широко используются в критичных к уровню надежности и отказоустойчивости компонентов областях: от комплексов диспетчеризации потоков воздушного транспорта и банковских систем до атомных электростанций и автоматизированных медицинских аппаратов для мониторинга за состоянием пациентов. Зачастую автоматизированная система воспринимается как лишенная недостатков оператора-человека при исполнении рутинных действий. При этом надежность аппаратной составляющей изучена достаточно широко: существует множество методик её оценки и повышения – например, параллелизация компонентов или подсистем. В свою очередь проблема моделирования и оценки надежности программного обеспечения до сих пор однозначно не решена. Именно поэтому зачастую оно становится самым слабым, - определяющим суммарный уровень надежности автоматизированной системы, - звеном. Кроме того, обнаруживаемые недостатки и уязвимости в аппаратной части, напрямую влияющие на общий уровень надежности системы, в большинстве случаев устраняются именно внесением корректив в программную составляющую, как требующих минимальных усилий и затрат от разработчиков и внедряющего персонала.
Каким образом можно получить адекватную и максимально объективную оценку надежности и качества программного обеспечения? К сожалению, широко распространенная и проверенная методика – тестирование программного продукта - даже широкомасштабное, лишь позволяет в той или иной мере повысить надежность путём устранения выявленных недостатков. На вопросы «Насколько надежен конечный продукт?» и «Какова вероятность сбоя определенного модуля?» оно ответа не даёт, а лишь косвенные предположения с достаточно высокой долей субъективизма.
Одной из важных составных частей современной теории управления является набор количественных методов исследования сложных процессов и явлений. В условиях совершенствования систем управления промышленностью и экономикой количественные методы придают процессу управления необходимую научную обоснованность, сводят до минимума элемент субъективности при выборе управленческих решений и позволяют в определенной мере оптимизировать как сам процесс управления, так и комплекс технических средств, обеспечивающих его осуществление [1]. В основе количественных методов лежат метрики — меры, позволяющая получить численное значение некоторого свойства программного обеспечения или его спецификаций.
Современная теория надежности программного обеспечения предлагает на выбор исследователя целый ряд самых разнообразных метрик и моделей надежности программного обеспечения. Подбирая различные метрики, подходящие к конкретному типу программного обеспечения, даже конкретному программному продукту, специалисты аналитическими методами делают выводы о надежности системы и о том, подходит ли она к конкретной области назначения[2]. Такой процесс хоть и является эффективным при достаточном уровне профессионализма экспертов, но практически не формализован (как следствие, трудно поддаётся автоматизации), и является достаточно дорогостоящим при высоком уровне субъективности выводов.
Если процесс получения выводов о надежности программного обеспечения по значениям различных его метрик формализовать в некоторую строгую методику, он станет намного эффективнее. Более того, при должном подходе, можно получить вероятностную характеристику надежности, определяющую возможность сбоя в определенном программном модуле на определенном участке кода. Для этого необходимо установить наличие связей между определенными метриками и надежностью программного продукта. Такие связи будут варьироваться для различных категорий программного обеспечения – в некоторых видах программных продуктов они будут выражаться сильнее, в некоторых слабее.
Помимо этого, многие метрики являются взаимно коррелированными, и оказывают совместное влияние на надёжность. Учитывая данный факт при построении вероятностной модели надежности, можно значительно усилить эффективность её работы.
Таким образом, универсальная комплексная метрика, подходящая для различных типов программного обеспечения, может быть получена совмещением различных уникальных наборов показателей, и введением поправочных коэффициентов (весов), формируемых на основе простых метрик и в зависимости от типа оцениваемого ПО и регулирующих степень значимости конкретных групп в общем комплексном показателе надежности. Одна из основных проблем получения такой метрики – отбор простых метрик, которые будут участвовать в вычислении такого показателя. Как было сказано выше, большинство из метрик – взаимно коррелированны, при этом в зависимости от коэффициента корреляции принимается решение о включении или не включении зависимых метрик в комплексный показатель. Коэффициент корреляции для двух показателей (являющихся в известной мере случайными):
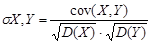 , (1)
, (1)
где D(X) и D(Y) – дисперсии парных величин; cov(X,Y) – их ковариация:
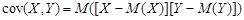 ,
,
где M(X) – математическое ожидание соответствующей величины.
При подсчете значения σ – парного коэффициента корреляции – будет получено значение от -1 до +1. Чем ближе модуль этого числа к 1, тем сильнее выражена корреляционная зависимость между метриками. Для тех пар метрик, которых он равен единице или близок к ней, достаточно включать в комплексный показатель одну из них. Для пар метрик с высокой и средней корреляцией необходимо вводить поправочные коэффициенты. Величины таких коэффициентов для разных типов программного обеспечения устанавливаются на основе усредненных показателей, но могут быть уточнены в результате экспериментальных исследований. Для этого по каждой метрике необходимо учесть в среднем до 100 результатов наблюдений. Подобный алгоритм подсчета комплексной метрики удобно смоделировать с использованием сетей доверия Байеса, закладывая в узлы полученные значения метрик и устанавливая связи между узлами с помощью полученных коэффициентов корреляции.
Оценка взаимной корреляции метрик и их связи с общей надежностью значительно затруднена в связи с неоднородностью природы определяющих метрики характеристик ПО. Поэтому для числового выражения связи между свойством ПО и некоторым показателем надежности (плотность сбоев, количество жалоб на сбои от пользователей и др.) необходимо ввести базовый коэффициент, определяющий такую связь, и единообразно отмасштабированный для всех метрик.
Если метрика является числовой (например, LOC), то для оценки коэффициента динамики изменения количественных показателей проекта в процессе его разработки в разрезе m-ной метрики для n-ной категории воспользуемся следующей формулой:
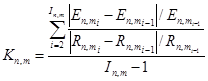 , (2)
, (2)
где Rn,mi – числовое значение n-ной метрики в i-м опыте проведенном на экспериментальном экземпляре программного обеспечения из m-й категории; En,mi – количество обнаруженных ошибок в программном коде, обнаруженных после изменения n-ной метрики на экспериментальном экземпляре программного обеспечения из m-й категории на i-м опыте; In,m – количество опытов, проведенных для n-й метрики на экспериментальном экземпляре программного обеспечения из m-й категории. При этом предполагается, что в ходе измерений количественный показатель (например, количество ошибок) оценивается набегающим результатом, то есть обнаруженные на предыдущих опытах ошибки включаются в результат текущего измерения независимо от состояния их исправления.
Очевидно, что формулу (2) уместно использовать лишь на гладких однонаправленных интервалах изменения значений метрик и показателей качества, что на практике встречается крайне редко. Для случаев, когда зависимость надежности от характеристики, показываемой метрикой, имеет место быть, но её характер меняется порогообразно, уместно свести результаты исследования поведения метрики в таблицу, где выделить интервалы однообразного изменения значения показателей надежности. Полученные данные в дальнейшем следует проанализировать, сделав выводы о причинах такого поведения показателя. В большинстве случаев связь показателя надежности и метрики (в случаях, когда она имеет место быть) меняет свой характер в следствие влияния характеристики, описываемой метрикой, коррелированной с рассматриваемой.
С учётом вышесказанного, эксперимент для выявления связи метрик с показателями надежности программного продукта для каждой категории программного обеспечения, по сути является наблюдением за ходом развития подходящего программного проекта. Необходимо при этом осуществлять запись значений гипотетически влияющих на надежность метрик и показателей надежности для каждой из версий программного обеспечения.
В приведенном эксперименте использовалась для анализа одна из операционных систем с открытым исходным кодом, сбор метрик и показателей проводился на ранних этапах развития продукта.
В качестве опытных метрик использовались: общее число строк кода (LOC), цикломатическая сложность, и максимальный показатель цикломатической вложенности. На начало эксперимента предполагалось, что, помимо прочих, характеристики данных метрик оказывают существенное влияние на показатели надежности.
Число строк кода – один из базовых показателей сложности программы, который принято принимать за точку отсчёта при анализе трудоёмкости написания программы.
Показатель цикломатической сложности является одним из наиболее распространенных показателей оценки сложности программных проектов. Данный показатель был разработан ученым Мак-Кейбом в 1976 г., относится к группе показателей оценки сложности потока управления программой и вычисляется на основе графа управляющей логики программы (control flow graph) [3]. Данный граф строится в виде ориентированного графа, в котором вычислительные операторы или выражения представляются в виде узлов, а передача управления между узлами – в виде дуг.
Показатель цикломатической сложности позволяет не только произвести оценку трудоемкости реализации отдельных элементов программного проекта и скорректировать общие показатели оценки длительности и стоимости проекта, но и оценить связанные риски и принять необходимые управленческие решения.
Упрощенная формула вычисления цикломатической сложности представляется следующим образом:
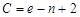 , (3)
, (3)
где e – число ребер, а n – число узлов на графе управляющей логики.
Как правило, при вычислении цикломатической сложности логические операторы не учитываются.
В процессе автоматизированного вычисления показателя цикломатической сложности, как правило, применяется упрощенный подход, в соответствии с которым построение графа не осуществляется, а вычисление показателя производится на основании подсчета числа операторов управляющей логики (if, switch и т.д.) и возможного количества путей исполнения программы. Такой подход использовался и при проведении эксперимента.
Цикломатическое число Мак-Кейба показывает требуемое количество проходов для покрытия всех контуров сильносвязанного графа или количества тестовых прогонов программы, необходимых для исчерпывающего тестирования по принципу «работает каждая ветвь».
Максимальная цикломатическая вложенность – «глубина» графа используемого при подсчете цикломатической сложности.
В качестве показателей надежности в эксперименте выступает количество ошибок, так или иначе упомянутых по отношению к конкретной версии программного обеспечения.
В ходе эксперимента преследуется цель подтвердить либо опровергнуть гипотезу о связи характеристик, выражаемых метриками, и показателей надежности программного проекта.
На рисунке 1 представлен график, на котором отражена динамика изменения размера программного кода (пунктиром показано значение прироста LOC от версии к версии в тысячах строк) и появления зарегистрированных для данной версии числа ошибок (сплошная кривая).
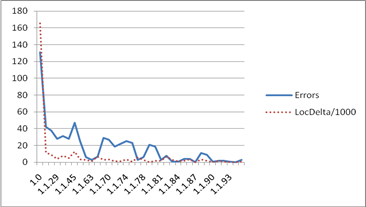
Рисунок 1 – график изменения размера кода и появления зарегистрированных ошибок в программе
На рисунке 2 представлен график изменения максимальной цикломатической вложенности для каждой версии программного продукта.
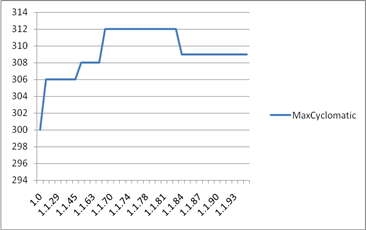
Рисунок 2 – график изменения максимальной цикломатической вложенности
На рисунке 3 представлен график изменения цикломатической сложности для каждой версии программного продукта.
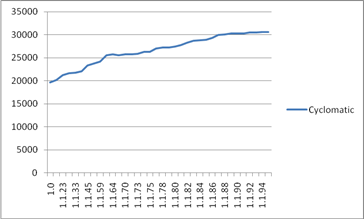
Рисунок 3 – график изменения цикломатической сложности
На рисунке 3 представлен график изменения цикломатической сложности для каждой версии программного продукта. Из результатов эксперимента видно, насколько ярко выражена зависимость между количеством добавляемого в программу кода и количеством вносимых в неё ошибок. Практически везде, где начинает «расти» график изменения LOC, увеличивается количество «релизовых» ошибок.
Соотнесём также данные на рисунке 1 и рисунке 2. Заметно, что рост максимальной цикломатической вложенности также происходит одновременно с «всплесками» числа ошибок. Эта метрика является полноценным отражением сложности программы, как правило, в динамике отражая и рост функциональности продукта. Очевидно, что в момент значительного расширения функционала продукта (сопряженного с увеличением сложности) происходит появление большого количества ошибок. Следует заметить, что «устоявшееся» значение максимальной цикломатической вложенности свидетельствует о том, что функционал приложения стабилизировался, и расширяется незначительно. Исходя из полученных в ходе эксперимента графиков и количество новых ошибок от релиза к релизу уменьшается и стабилизируется. Поведение цикломатической сложности на рисунке 3 в целом соотносится с метрикой LOC. Колебания её значений также приходятся на всплески количества обнаруженных в релизе ошибок.
Эксперимент доказал, что многие метрики программного обеспечения могут быть использован для оценки надежности программных продуктов. Однако ряд метрик обладает схожим поведением, что является следствием их взаимной коррелированности. Необходимо также расширить эксперимент, включив в него дополнительные показатели.
В конечном итоге экспериментальные данные будут использованы для формирования комплексной метрики оценки надежности программного обеспечения.
Литература:
1. Трухаев Р.И. Модели принятия решений в условиях неопределенности. М.: Наука, 1981.
2. Kan, Stephen H. Metrics and models in software quality engineering / Addison-Wesley —2nd ed, 2002.
3. Новичков А. Метрики кода и их практическая реализация в IBM Rational ClearCase [Электронный ресурс] // CM-Консалт – Консалтинг в области разработки ПО [сайт]. URL: http://www.cmcons.com/articles/CC_CQ/code_metrics_clearcase/ (дата обращения: 01.12.2009).







