В условиях современной рыночной системы успешными являются те предприятия, которые могут в кратчайшие сроки перейти на выпуск новой продукции с минимальными потерями. Продолжительные производственные циклы не позволяют вовремя зафиксировать падение спроса, осложняют связь производства с требованиями рынка. Преодоление данных проблем требует нового подхода к управлению временем производственных и управленческих процессов на швейных предприятиях.
Объектом исследования в данной работе являлся раскройный цех, который служит связующим звеном между подготовительным и швейными цехами предприятия. Его основная задача состоит в ритмичном снабжении деталями кроя швейных цехов. Для решения этой задачи необходимо точно спрогнозировать длительность производственного цикла (ДПЦ) [1].
Прогнозирование (планирование) является механизмом управления производством и одной из главных функций, которая регламентирует определенный порядок, последовательность осуществления намеченной на конкретный период программы развития предприятия.
Так как прогнозирование устанавливает конкретные сроки выполнения различных операций производства, то ДПЦ является одним из важнейших факторов, который влияет на такие данные как даты поставки материалов, договоренность с оптовыми покупателями, объём незавершенного производства и т.п. В связи с этим, необходимо наиболее точно установить ДПЦ.
Анализ опубликованных по данной проблеме работ показал, что существующие методы расчета ДПЦ [2] в условиях неопределенности и динамизма внешней и внутренней среды предприятия начинают давать сбой. Аналитические модели расчета ДПЦ не всегда соответствуют фактическому значению производственного цикла в реальных условиях. На точность расчётов значительное влияние оказывает воздействие случайных факторов (невыход исполнителя на работу, задержка подачи материалов, поломка оборудования и т.д.), вследствие которых фактическая ДПЦ оказывается значительно больше расчётной, что приводит к простою оборудования и рабочих, увеличению запасов незавершённого производства и, в конечном счете, увеличивает себестоимость изделий.
Следовательно, необходимо применение таких систем, которые могут не только выполнять однажды запрограммированную последовательность действий над заранее определенными данными, но и способны анализировать вновь поступающую информацию, находить в ней закономерности и учитывать воздействие случайных факторов.
Наилучшим образом для решения подобных задач зарекомендовали себя нейронные сети – самообучающиеся системы, имитирующие деятельность человеческого мозга. Это математические модели, а также их программные или аппаратные реализации, построенные по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма [3].
Нейронные сети не программируются в привычном смысле этого слова, они обучаются. Возможность обучения - одно из главных преимуществ нейронных сетей перед традиционными алгоритмами. Технически обучение заключается в нахождении коэффициентов связей между нейронами. В процессе обучения нейронная сеть способна выявлять сложные зависимости между входными данными и выходными, а также выполнять обобщение. Это значит, что, в случае успешного обучения, сеть сможет вернуть верный результат на основании данных, которые отсутствовали в обучающей выборке.
В данной работе решена задача прогнозирования ДПЦ с использованием нейронной сети и реализована с помощью отечественной аналитической платформы «Deductor» (компания BaseGroup Labs(РФ, Рязань)).
Перед построением нейронной сети проведен корреляционный анализ, который позволяет устранить незначащие факторы. При пороге значимости 0,05 все факторы (входные значения) оказались значимыми и имеют положительные значения, т.е. при увеличении входных значений будет увеличиваться и ДПЦ.
На следующем этапе построена нейронная сеть. Количество входных и выходных нейронов известно, каждый из входных нейронов соответствует одному из системных (количество полотен в настиле, время настилания одного полотна, количество секционных настилов и т.д.) и случайных факторов (технологические дефекты на различных участках обработки, поломка оборудования и т.д.), влияющих на ДПЦ, нейрон в выходном слое представляет собой прогнозируемую величину ДПЦ.
Неизвестным остается лишь число скрытых слоев и число нейронов в скрытом слое (рис. 1,2).
|
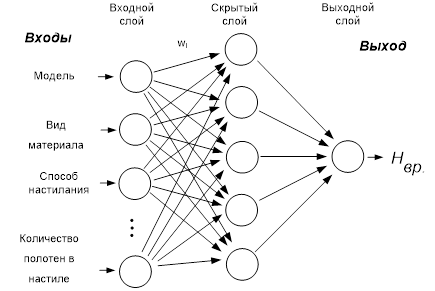
Рис. 1 - Структура нейронной сети
Для алгоритма обратного распространения ошибки рекомендуется один скрытый слой, большее количество слоев приводит к переобучению нейронной сети, когда сеть полностью распознает примеры из обучающего множества, подаваемые для обучения, и дает большую ошибку при подаче на его входы примеры тестового множества.
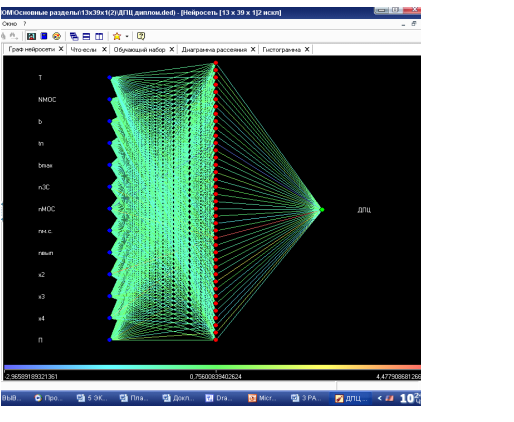
Рис. 4 Граф нейронной сети в аналитической платформе «Deductor»
Для определения количества нейронов в скрытом слое использовалась теорема Колмогорова, которая служит математической основой для нейронных сетей и заключается в следующем: любая непрерывная функция, определенная на n-мерном единичном кубе, может быть представлена в виде суммы 2n+1 суперпозиций непрерывных и монотонных отображений единичных отрезков. То есть верхняя граница числа нейронов в скрытом слое не должна быть более: 2n+1 (n – количество входов) [3].
Обучение нейронной сети производилось методом «с учителем» - это такой способ постановки эксперимента, в ходе которого система обучается с помощью примеров «вход-эталон». Между входами (факторами, влияющими на ДПЦ) и эталонным выходом (ДПЦ) может существовать некоторая зависимость, но она не известна. Известна только конечная совокупность прецедентов, называемая обучающей выборкой. На основе этих данных требуется восстановить зависимость, то есть построить алгоритм, способный для любого объекта выдать достаточно точный ответ.
Процедура обучения искусственной нейронной сети сводится к процедуре коррекции весов её связей. Целью процедуры является коррекция весов – т.е. минимизация функции ошибки E:
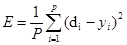 (1)
(1)
где P - количество обработанных нейронной сетью примеров;
yi - реальный выход нейронной сети;
di - желаемый (идеальный) выход нейронной сети.
На сколько успешно прошло обучение нейронной сети показывает диаграмма рассеяния (рис. 3).
На диаграмме рассеяния отображаются выходные значения для каждого из примеров обучающей выборки (координаты которых по оси Х - это значение выхода на обучающей выборке (эталон), а по оси Y - значение выхода, рассчитанное обученной моделью на том же примере). Прямая диагональная линия представляет собой линию идеальных значений. Чем ближе точка к этой линии, тем меньше ошибка модели. Две пунктирные линии обозначают верхнюю и нижнюю границы доверительного интервала. Так как все точки близки к идеальным значениям, то это позволяет сделать вывод о хорошем качестве обучения нейросети.
Также анализ построенной нейросети проводился с помощью способа отображения данных в форме «что-если», т.е. на входы подавались значения, которые не использовались при обучении нейронной сети. Так как относительная ошибка полученных значений не превысила 1%, то это позволяет сделать вывод о хороших результатах обучения и возможности применения данной нейронной сети при прогнозировании ДПЦ в раскройном производстве.
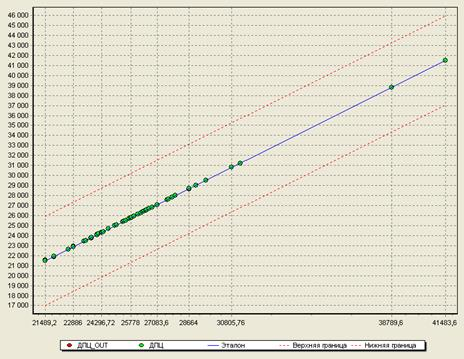
Рис. 3 Диаграмма рассеяния
Литература:
1. Мокеева Н.С., Заев В.А., Сенникова Е.В. Пути сокращения длительности производственного цикла в условиях гибкого раскройного производства // Известия вузов. Северо-Кавказский регион. Технические науки, 2008. - № 5. – С.104 -106.
2. Файнгольд М.Л., Кузнецов Д.В. Проблемы совершенствования методики расчета длительности производственного цикла / Под ред. М.Л. Файнгольд. – Владимир: Издательство ВГПУ, 2001. – 47с.
3. Мокеева Н.С., Петрова Е.В. (Сенникова Е.В.) Повышение качества технологической подготовки производства швейных изделий путем экспресс-расчета норм времени на операции раскройного цеха // Молодой ученый, 2009. - № 10. – С. 71 -75.







