Учет дискретно-распределенных параметров высоковольтной обмотки при расчете ультразвукового трансформатора

В электромагнитном отношении ультразвуковой высоковольтный трансформатор представляет собой сложную систему с дискретно-распределенными между его элементами его конструкции магнитными и электрическими связями. Магнитные связи между обмотками в целом, а также между их частями, которые разделены емкостными связями, учитываются коэффициентом взаимной индукции. Электрические связи учитываются емкостями между магнитной системой и первичной обмоткой, между витками обмоток, между первичной и вторичной обмотками, между вторичной обмоткой и  магнитной системой. Распределенный характер носит также сопротивление обмоток, сопротивление потерь на вихревые токи, на гистерезис и в изоляции обмоток [1].

Для  описания электромагнитных процессов в высоковольтной обмотке ультразвукового трансформатора применен инструмент разностных уравнений [2]. Разностные уравнения обычно применяются: 1) для аппроксимации дифференциальных уравнений с частными производными; 2) для решения задач, представляющих модели с дискретными переменными. Величины n_Г , n_P и n_C  есть целые числа и изменяются дискретно, то есть  имеем второй случай.          Решение этих уравнений осуществляется методом суммирования – аналогом интегрирования.

На рис. 1а приведено реальное распределение межвитковых «С₁», межслоевых «С₁^’»  и межсекционных «С₂»  емкостей и индуктивностей рассеяния «L₁»  и «L₁^’»  высоковольтной обмотки трансформатора. Величина n_Г определяет число секций(галет) высоковольтной обмотки, величины n_P и n_C  - число витков в одном ряду секции и число рядов в каждой секции. Распределенные параметры образуют множество контуров,  контура эти имеют три разновидности:

1)      контур «э.д.с. е_в – конденсатор С₁ – индуктивность L₁»;

2)      контур «сумма э.д.с. 2ke_в – конденсатор С₁^’ – индуктивность L₁^’»;

3)      контур «сумма э.д.с. n_p(n_c-1)e_в – конденсатор С₂».

 

Рассмотрим контур « э.д.с. e_в – конденсатор С₁ – индуктивность L₁» по которому замыкается ток 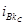 показан на рис.1б.  Число контуров по которым замыкается этот ток равно числу витков  высоковольтной обмотки трансформатора w₂=n_C.n_P.n_{Г .}

 

 

б)

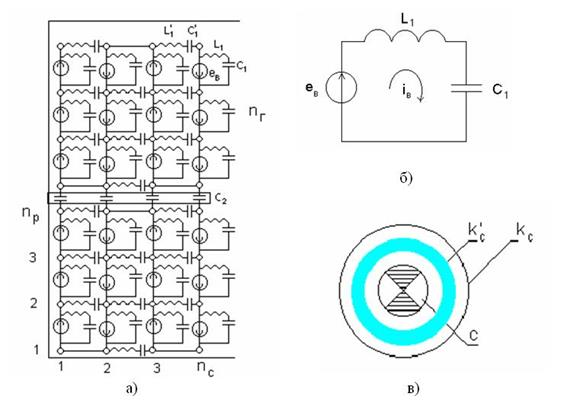
Рис. 1. а) распределение межвитковых емкостей и индуктивностей рассеяния высоковольтной обмотки; б) Контур «э.д.с. е_в – конденсатор С₁ – индуктивность L₁»; в) Поперечный разрез высоковольтной обмотки трансформатора: с – сердечник,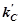- номер слоя ()

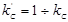Этот ток равен:

 .

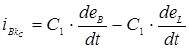Э.д.с., наводимая в одном витке  и равная

 ,

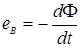где Ф - основной поток трансформатора.

            Э.д.с. е_L  зависит  от изменения потока рассеяния, величина которого в свою очередь зависит от числа охватываемых им слоев и может быть приставлена следующим образом, рис 1.в.

Поток рассеяния высоковольтной катушки можно представить в виде

,

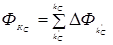где 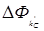магнитный поток, возникающий при охватывании  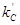слоя и определяемый следующим разностным уравнением:

 

 ,

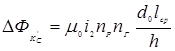где m₀ – магнитная проницаемость воздуха, m₀ = 4×p×10^-7 Гн/м; i₂ – ток вторичной обмотки;

d₀ – диаметр изолированного провода вторичной обмотки; l_СР – средняя длина витка вторичной обмотки; h – высота вторичной обмотки.

 Произведя суммирование получим:

.

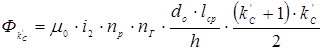Отсюда магнитный поток рассеяния 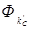 равен

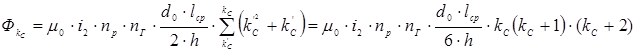
тогда э.д.с. е_L  равна

.

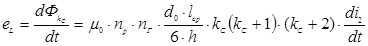Подставив в выражение (1) значение  е_L  получим:

_.

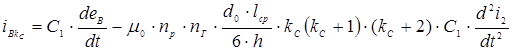                М.д.с. наводимая токами данного вида контуров, определяется следующим разностным уравнением:

 .

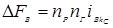Суммирование этого разностного уравнения позволяет получить суммарную м.д.с., наводимую этими токами:

.

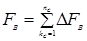После подстановки получим

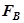
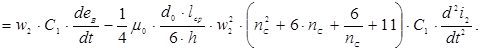
2) Контур «сумма э.д.с. 2ke_в – конденсатор С₁ ^‘– индуктивность L₁^’» изображен на рисунке 2. По данному  контуру замыкается ток:

.

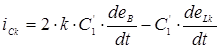После замены е_Lk выражение для тока i_ck имеет следующее выражение:

_.

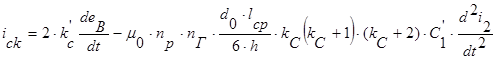Количество контуров по которым замыкается данный ток равно (n_p-1)×(n_c1)×n_Г .

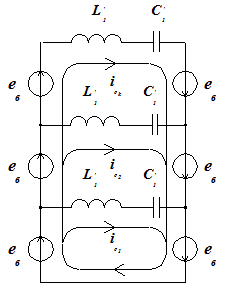
Рис.2. Контур тока i_ck

М.д.с.  F_kp определится суммированием следующего  разностного уравнения:

.

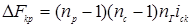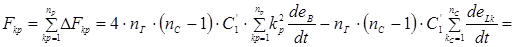
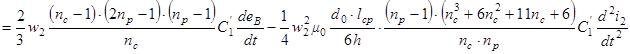
Емкости С₁  и С₁^’  в первом приближении равные между собой, рассчитываем, обычными методами теории электростатического поля. Опуская промежуточные выкладки, получаем

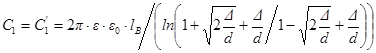
где d – диаметр неизолированного провода, D - толщина изоляции провода.

3) Контур «сумма э.д.с. n_p(n_c-1)×e_B – конденсатор С₂», по которому замыкается ток i_Г  изображен на рисунке 3.  Ток, замыкающийся по этому контуру равен:

.

iГ3

iГ2

iГ1

eв

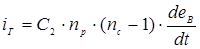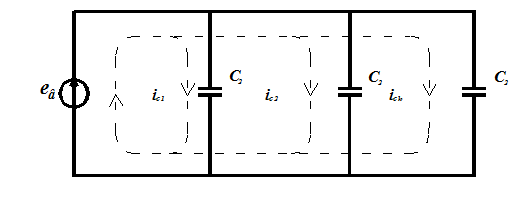
Рис.3. Контур тока i_Г

Так как количество контуров данного вида равно . n_Г(n_c-1), то м.д.с. данных контуров определится следующим разностным уравнением:

                                                            .

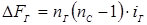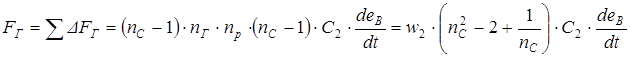      Межсекционная емкость С₂ обычными методами теории электростатического поля и равна:

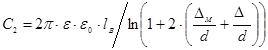
Суммарная  м.д.с. , создаваемая токами i_B, i_Ck, i_Г , составляет величину:

                                             

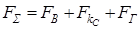
После подстановки выведенных ранее выражений для F_B , F_kc и F_Г   и разделив слагаемые, относящиеся к 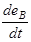 и 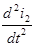, получаем:

                                       .                                  

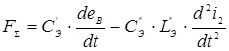Данное выражение позволяет представить следующую схему замещения  трансформатора (рис. 4).

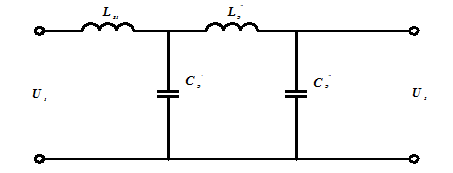
Рис. 4. Схема замещения ультразвукового высоковольтного трансформатора

Для оценки влияния дискретно-распределенных параметров ультразвукового высоковольтного трансформатора, промоделируем полученную схему его замещения при помощи программного пакета MicroCap 9. Для этого при помощи примитивов пакета создается схема замещения трансформатора, на вход которой подается импульсное напряжение с амплитудой сигнала 150В и частотой следования импульсов 20 кГц.

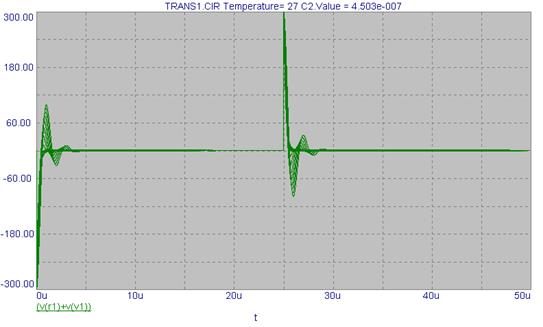Сравнивая сигналы напряжения на входе и на выходе схемы замещения (рис.5), приходим к выводу, что трансформируемый импульс искажается, а значит, влияние дискретно-распределенных параметров негативно сказывается на прохождении импульса. Очевидно, что чем меньше величина элементов схемы замещения, тем меньше искажений будет испытывать трансформируемый импульс.

Рис.5. Разница между сигналами на входе V(1) и выходе V(r1) схемы замещения  высоковольтного ультразвукового трансформатора

Данная методика  была применена для расчета ультразвуковых высоковольтных трансформаторов технологических установок с нелинейной емкостной нагрузкой, в частности, озонаторов и плазмохимических активаторов полиолефиновых пленок.

Литература:

1.      Русин Ю. С. Трансформаторы звуковой и ультразвуковой частоты. Л.: Энергия, 1973. 152 с.

2.      Шапиро С.В., Саенко А.Г. Резонансные явления в источнике питания активатора полимерных материалов // Электротехнические комплексы и системы: сборник научных трудов. Уфа: УГАТУ, 2001. – с. 66-70.