В научной и практической деятельности человека значительное место занимают теоретические методы изучения различных объектов и процессов окружающего мира. Несмотря на высокую эффективность теоретических методов, при рассмотрении конкретных технологических проблем, например, в условиях действующего производства, приходятся инженерные задачи, решить которые невозможно без организации и проведения экспериментальных исследований.
Применение математических методов при проведении экспериментов является одним из подходов к решению задач оптимального проектирования в системах автоматического управления и оценки эффективности функционирования системы. К сожалению, работа экспериментатора настолько хаотична и неорганизованна, а ее эффективность так мала, что полученные результаты не в состоянии оправдать даже тех средств, которые были израсходованы на проведение опытов. Поэтому вопросы организации эксперимента, снижения затрат на его проведение и обработку полученных результатов являются весьма и весьма актуальными.
В системах автоматического управления математические методы используются при планирования экспериментов для выявления зависимостей между показателями качества – параметрами и факторами, определяющими их численную величину. Факторы, влияющие на технологический процесс, определяют оптимальные условия работы системы управления. Зависимость, как правило, определяется на основании моделей, полученных на основе теории активного и пассивного экспериментов.
Планирование эксперимента при разработке систем автоматического управления рассмотрено на примере системы измерения параметров газового потока для технологического процесса гранулирования суспензий методом распылительной сушки. Для проведения экспериментальных исследований использовалась лабораторная установка измерения параметров газового потока – макет установки гранулирования суспензий.
Лабораторная установка включает в себя два датчика давления, датчик влажности, и термопреобразователь сопротивления. Исследуемыми параметрами, характеризующими ход технологического процесса гранулирования суспензий, являются давление на входе и выходе измерительной линии, расход несущей среды, температура и влажность газового потока.
Планирование эксперимента существенно способствует повышению производительности и надежности полученных результатов. Одним из методов планирования эксперимента является разработка полного факторного эксперимента.
В рассматриваемой системе, параметрами, характеризующими процесс гранулирования методом распылительной сушки, являются показания первичных измерительных приборов, а именно:
y1 (P1) – измеренное значение датчика давления №1, кПа;
y2 (P2) – измеренное значение датчика давления №2, кПа;
y3 (T) – измеренное значение датчика температуры, °С;
y4 (W) – измеренное значение датчика влажности, %.
По результатам предварительного анализа значимости факторов (степени влияния на функцию), произведено ранжирование и исключение малозначащих факторов рассматриваемой системы. Установлено, что факторами, определяющими процесс гранулирования суспензий, являются:
x1 (Tгаза) – температура газовой среды, °С;
x2 (Wгаза) – относительная влажность газовой среды, %;
x3 (Pгаза) – давление газа, кПа;
x4 (Q) – массовый расход, кг/с.
Интервал варьирования каждого фактора определен в соответствии с методикой выполнения измерений при использовании лабораторной установки и условий гранулирования суспензий методом распылительной сушки.
На основании имеющихся сведений, выбранные уровни и интервалы варьирования факторов представлены в таблице 1.
Таблица1. Уровни факторов и интервалы варьирования факторов
|
Факторы |
Уровень |
Интервал варьирования |
Размерность |
||
|
–1 |
0 |
+1 |
|||
|
x1 |
50 |
75 |
100 |
25 |
°С |
|
x2 |
30 |
55 |
80 |
25 |
% |
|
x3 |
80 |
95 |
110 |
15 |
кПа |
|
x4 |
0,1 |
0,3 |
0,5 |
0,2 |
кг/с |
Количество уровней факторов определяет количество опытов в соответствии с выражением [2, с. 14]:
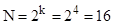 , (1)
, (1)
где N – число опытов, k – число факторов.
Для повышения надежности оценки при проведении эксперимента дополнительно проведено 4 опыта в центре плана эксперимента. В соответствии с условиями проведения эксперимента составлена матрица планирования эксперимента. С целью исключения систематических ошибок эксперименты рандомизированы во времени, последовательность опытов определена таблицей случайных чисел [1, с. 133]. Матрица планирования эксперимента приставлена в таблице 2.
Таблица 2. Матрица планирования эксперимента
|
№ опыта |
x1 |
x2 |
x3 |
x4 |
x1x2 |
x1x3 |
x1x4 |
x2x3 |
x2x4 |
x3x4 |
y1 |
y2 |
y3 |
y4 |
||||
|
1 |
-1 |
50 |
-1 |
30 |
-1 |
80 |
-1 |
0,1 |
1 |
1 |
1 |
1 |
1 |
1 |
80,90 |
80,80 |
50,00 |
31,5 |
|
2 |
1 |
100 |
-1 |
30 |
-1 |
80 |
-1 |
0,1 |
-1 |
-1 |
-1 |
1 |
1 |
1 |
80,97 |
80,63 |
97,77 |
28,4 |
|
3 |
-1 |
50 |
1 |
80 |
-1 |
80 |
-1 |
0,1 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
80,93 |
80,40 |
48,69 |
78,3 |
|
4 |
1 |
100 |
1 |
80 |
-1 |
80 |
-1 |
0,1 |
1 |
-1 |
-1 |
-1 |
-1 |
1 |
79,90 |
79,80 |
99,01 |
81,3 |
|
5 |
-1 |
50 |
-1 |
30 |
1 |
110 |
-1 |
0,1 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
109,70 |
108,00 |
45 |
27,4 |
|
6 |
1 |
100 |
-1 |
30 |
1 |
110 |
-1 |
0,1 |
-1 |
1 |
-1 |
-1 |
1 |
-1 |
111,10 |
107,90 |
96 |
30,5 |
|
7 |
-1 |
50 |
1 |
80 |
1 |
110 |
-1 |
0,1 |
-1 |
-1 |
1 |
1 |
-1 |
-1 |
107,80 |
106,10 |
49 |
83,1 |
|
8 |
1 |
100 |
1 |
80 |
1 |
110 |
-1 |
0,1 |
1 |
1 |
-1 |
1 |
-1 |
-1 |
112,30 |
110,80 |
98 |
82,1 |
|
9 |
-1 |
50 |
-1 |
30 |
-1 |
80 |
1 |
0,5 |
1 |
1 |
-1 |
1 |
-1 |
-1 |
78,30 |
80,40 |
48 |
28,5 |
|
10 |
1 |
100 |
-1 |
30 |
-1 |
80 |
1 |
0,5 |
-1 |
-1 |
1 |
1 |
-1 |
-1 |
79,50 |
83,10 |
99 |
32,3 |
|
11 |
-1 |
50 |
1 |
80 |
-1 |
80 |
1 |
0,5 |
-1 |
1 |
-1 |
-1 |
1 |
-1 |
84,00 |
82,30 |
45 |
79,1 |
|
12 |
1 |
100 |
1 |
80 |
-1 |
80 |
1 |
0,5 |
1 |
-1 |
1 |
-1 |
1 |
-1 |
81,30 |
82,40 |
95,98 |
81,5 |
|
13 |
-1 |
50 |
-1 |
30 |
1 |
110 |
1 |
0,5 |
1 |
-1 |
-1 |
-1 |
-1 |
1 |
112,30 |
111,70 |
46,98 |
29,4 |
|
14 |
1 |
100 |
-1 |
30 |
1 |
110 |
1 |
0,5 |
-1 |
1 |
1 |
-1 |
-1 |
1 |
112,30 |
107,90 |
96,66 |
28,700 |
|
15 |
-1 |
50 |
1 |
80 |
1 |
110 |
1 |
0,5 |
-1 |
-1 |
-1 |
1 |
1 |
1 |
109,30 |
106,70 |
46,13 |
81,2 |
|
16 |
1 |
100 |
1 |
80 |
1 |
110 |
1 |
0,5 |
1 |
1 |
1 |
1 |
1 |
1 |
110,70 |
116,30 |
97,45 |
80,5 |
|
17 |
0 |
75 |
0 |
55 |
0 |
95 |
0 |
0,3 |
0 |
0 |
0 |
0 |
0 |
0 |
93,50 |
92,90 |
73,96 |
53,0 |
|
18 |
0 |
75 |
0 |
55 |
0 |
95 |
0 |
0,3 |
0 |
0 |
0 |
0 |
0 |
0 |
92,10 |
92,00 |
75,86 |
54,0 |
|
19 |
0 |
75 |
0 |
55 |
0 |
95 |
0 |
0,3 |
0 |
0 |
0 |
0 |
0 |
0 |
93,60 |
94,20 |
76 |
55,3 |
|
20 |
0 |
75 |
0 |
55 |
0 |
95 |
0 |
0,3 |
0 |
0 |
0 |
0 |
0 |
0 |
93,80 |
93,70 |
75,00 |
55,1 |
Проверка воспроизводимости эксперимента помощью критерия Кохрена (G–критерия) [2, с. 17]:
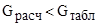 , (2)
, (2)
где 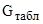 – табличное значение критерия Кохрена;
– табличное значение критерия Кохрена; 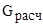 – расчетное значение критерия Кохрена, что подтвердила равноточность измерений.
– расчетное значение критерия Кохрена, что подтвердила равноточность измерений.
С целью определения степени влияния факторов на измеряемые параметры, рассчитаны коэффициенты модели:
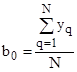 ; (3)
; (3)
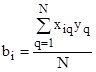 , (4)
, (4)
Полученные значения коэффициентов по выражениям (3), (4) представлены в таблицы 3.
Таблица 3. Коэффициенты модели
|
Коэффициент |
y1 |
y2 |
y3 |
y4 |
|
b0 |
95,706 |
95,327 |
72,416 |
55,238 |
|
b1 |
0,302 |
0,777 |
25,067 |
0,425 |
|
b2 |
0,073 |
0,273 |
-0,009 |
25,650 |
|
b3 |
14,981 |
14,098 |
-0,514 |
0,125 |
|
b4 |
0,256 |
1,023 |
-0,517 |
-0,088 |
|
b12 |
-0,031 |
0,948 |
0,136 |
0,038 |
|
b13 |
0,610 |
0,523 |
0,058 |
-0,337 |
|
b14 |
-0,315 |
0,298 |
0,306 |
0,175 |
|
b23 |
-0,735 |
0,277 |
0,751 |
0,713 |
|
b24 |
0,290 |
0,302 |
-0,751 |
-0,225 |
|
b34 |
0,206 |
0,202 |
0,419 |
-0,325 |
Коэффициенты, вычисленные по результатам эксперимента, являются показателями степени влияния факторов. Степень значимости коэффициентов модели определена по критерию Стьюдента с вероятностью Р=0,95:
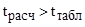 . (5)
. (5)
В соответствии с F-критерием Фишера, необходимо определить дисперсия воспроизводимости эксперимента 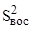 [1, с. 149]. В некоторых случаях дублирование опытов осуществляется только для одной из q- строк матрицы планирования или в центре плана эксперимента. В таком случае дисперсия воспроизводимости
[1, с. 149]. В некоторых случаях дублирование опытов осуществляется только для одной из q- строк матрицы планирования или в центре плана эксперимента. В таком случае дисперсия воспроизводимости 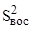 находится как построчная дисперсия
находится как построчная дисперсия 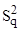 , и определяется выражением:
, и определяется выражением:
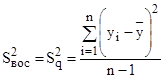 , (6)
, (6)
где 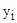 – значения показателя качества в центре плана эксперимента;
– значения показателя качества в центре плана эксперимента; 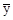 – среднее значение показателя качества из n опытов; N – число опытов в центре плана эксперимента (n=4). Результаты вычислений представлены в таблице 4.
– среднее значение показателя качества из n опытов; N – число опытов в центре плана эксперимента (n=4). Результаты вычислений представлены в таблице 4.
|
Таблица 4 |
||||
|
|
y1 |
y2 |
y3 |
y4 |
|
S2вос |
0,603 |
0,927 |
0,882 |
1,137 |
В соответствии с t-критерием Стьюдента, для каждого коэффициента модели необходимо определить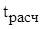 :
:
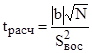 . (7)
. (7)
Табличное значение 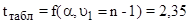 при α=0,05 и n=4 [2, с.24].
при α=0,05 и n=4 [2, с.24].
В результате анализа значимости коэффициентов, выявлено, что вероятностью Р=0,95 значимыми будут следующие коэффициенты:
для y1: b0, b3, b13, b23;
для y2: b0, b1, b3, b4, b12;
для y3: b0, b1, b23, b24;
для y4: b0, b2, b23 .
Математическая модель эксперимента имеет вид полинома первого порядка:
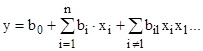 , (8)
, (8)
В соответствии с полученными результатами, исключая незначимые коэффициенты, математическая модель будет иметь вид:
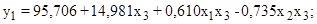 (9)
(9)
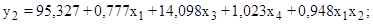 (10)
(10)
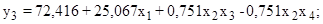 (11)
(11)
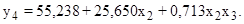 (12)
(12)
Полученная модель, представленная выражениями (9) – (12), приведена к нормальному виду:
P1=95,706+14,981Pгаза+0,610TгазаPгаза - 0,735WгазаPгаза; (13)
P2=95,327+0,777Tгаза+14,098Pгаза+1,023Q+0,948TгазаWгаза; (14)
T=72,416+25,067Тгаза+0,751WгазаРгаза - 0,751WгазаQ; (15)
W=55,238+25,650Wгаза+0,713WгазаPгаза. (16)
Проверка адекватности разработанной модели, представленной выражениями (13) – (16) выполнена по F – критерию Фишера.
Остаточная дисперсия определяется по формуле:
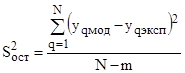 , (17)
, (17)
где 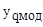 – величина показателя качества для q-го опыта (рассчитывается при подстановке в полученную модель вычисленных значений
– величина показателя качества для q-го опыта (рассчитывается при подстановке в полученную модель вычисленных значений 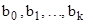 и значений
и значений 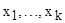 для данного опыта);
для данного опыта); 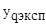 - экспериментально полученное значение y в q – м опыте; m – общее число значимых коэффициентов модели, включая и коэффициент b0.
- экспериментально полученное значение y в q – м опыте; m – общее число значимых коэффициентов модели, включая и коэффициент b0.
Предварительно вычислим значения yмод по выражениям модели (9) – (12), подставляя вместо x1…xk значения -1 или +1 из таблицы 2.
Проверка гипотезы проводится с помощью дисперсионного отношения F – Фишера [1, с. 149]:
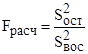 . (18)
. (18)
В таком случае, определим Fрасч для каждого из параметров:
для y1: 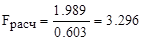 ; для y2:
; для y2: 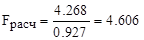 ;
;
для y3: 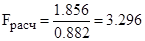 ; для y4:
; для y4: 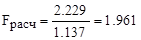 .
.
С целью проверки условия воспроизводимости модели:
Fрасч<Fтабл, (19)
определено Fтабл = f(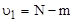 ,
,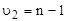 ) при α=0,05 [1, с.152]:
) при α=0,05 [1, с.152]:
для y1 Fтабл =(v1=12, v2=3) = 8,74; для y2 Fтабл = (v1=11, v2=3) = 8,76;
для y3 Fтабл = (v1=12, v2=3) = 8,74; для y4 Fтабл = (v1=13, v2=3) = 8,74.
Таким образом, согласно выражения (19), для y1, y2, y3, y4, с вероятностью 0,95 модель представленная выражениями (13) – (16), считается адекватной экспериментальным данным.
Полученные коэффициенты в процентном соотношении влияния на параметры представлены в таблице 7:
Таблица 7. Оценка влияния факторов на параметры (%).
|
|
||||||||||||
|
Тгаза |
Wгаза |
Pгаза |
ТгазаWгаза |
ТгазаPгаза |
TгазаQ |
WгазаPгаза |
WгазаQ |
PгазаQ |
W2газа |
|||
|
|
|
91,76 |
|
|
3,74 |
|
|
-4,5 |
|
|
||
|
4,61 |
|
83,69 |
6,07 |
5,63 |
|
|
|
|
|
|
||
|
94,35 |
|
|
|
|
|
|
2,83 |
-2,83 |
|
|
||
|
|
97,3 |
|
|
|
|
|
2,7 |
|
|
|
||
Знак минус свидетельствует о том, что с увеличением данного фактора, точность определения данного параметра падает [2, с. 25].
Таким образом, использование ПФЭ при разработке САУ позволяет определить степень влияния факторов на выходные параметры системы. Применение данного подхода при разработке САУ позволяет разработать гибкие стратегии управления и комплексной оценки ситуаций, реализуемые в прикладных ИС САУ.
Литература
1. Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий. – М.: НАУКА, 1976.
2. Захаров Ю.В. Математическое моделирование в технологии электронных средств. – Й-Ола: МарГТУ, 2003.







