Модель всегда является приближенной и рассчитанные по ней параметры отличаются от действительных, что является причиной затрат времени и других ресурсов на ее доводку. Поэтому проблема повышения степени адекватности математических моделей является одной из важнейших при проектировании, в т.ч. при оптимизации (структурной и параметрической).
Известны различные пути повышения степени адекватности моделей. Один из них заключается в более тщательном исследовании и более детализированном математическом описании всех особенностей рабочего процесса в изделии. Он используется при уточнении существующих методик расчета. Другой путь повышения степени адекватности – идентификация математической модели по результатам испытаний. При идентификации варьируются различные параметры математической модели, и уточнение ее получается только за счет изменения их величины без увеличения сложности модели [1].
Цель идентификации – уменьшение расхождений между результатами испытаний изделия и расчета по модели без изменения ее структуры (предложенные в данной работе методы позволяют производить и структурную идентификацию модели), а только за счет уточнения значений ряда параметров. Они называются варьируемыми параметрами или факторами и выбираются из числа наименее достоверных параметров математической модели. Испытания изделия проводятся на различных режимах с измерением возможно большего количества параметров. На этих же режимах производится расчет по модели. Разница между экспериментальным и расчетным значениями параметра называется невязкой. Она должна быть минимальной во всех измерениях (в многомерном варианте используется функционал невязок, например в виде свертки). Поэтому с помощью численных методов минимизируется функционал невязок. Например, при использовании МНК (метода наименьших квадратов) минимизируется сумма квадратов взвешенных невязок с помощью изменения поправок к варьируемым параметрам. Поправки обычно не получаются малыми и приходится делать несколько последовательных приближений.
Предложенные в данной работе методы позволяют производить не только параметрическую, но и структурную идентификацию моделей. При разработке математической модели двигателя использовались экспериментальные данные, позволившие идентифицировать характеристики его узлов.
Статическая характеристика установки позволяет получить характеристики узлов двигателя в широком диапазоне режимов, необходимом для исследования динамических характеристик. Экспериментальная динамическая характеристика представляет собой зависимость расхода топлива, давления воздуха за компрессором, ускорения ротора от частоты вращения ротора.
В настоящее время признано, что имитационные модели (ИМ) являются эффективным средством исследования и решения сложных проектно-доводочных задач, проведения разнообразных компьютерных экспериментов, организованных по аналогии со стендовыми испытаниями. Обычно ИМ создают и используют в среде моделирования, имеющей пре- и постпроцессор, решатель и библиотеку структурных элементов.
При моделировании газотурбинных двигателей и установок одним из важных вопросов является выбор достаточно точного и эффективного способа представления характеристик узлов двигателя: вентиляторов и компрессоров, камер сгорания, турбин и др. Несмотря на то, что этой проблеме посвящено значительное число работ, она является актуальной и сейчас, поскольку к новым универсальным методам построения математических моделей предъявляются высокие, зачастую противоречивые требования к форме представления характеристик узлов.
Достоверность получаемых с помощью ИМ результатов зависит от того, насколько адекватна модель моделируемому реальному объекту (в данном случае энергоустановке) и моделируемому процессу. Оценку степени (или области) адекватности проводят по-разному, но наиболее представительной является оценка на основе сопоставления результатов моделирования с результатами эксперимента.
Газотурбинная энергетическая установка ГТЭ10/95 предназначена для электро- и теплоснабжения жилых массивов, предприятий промышленности, объектов строительства, в отдаленных от энергосистем районах, а также в качестве дополнительного источника на крупных ТЭЦ для покрытия пиковых нагрузок. ГТЭ 10/95 номинальной электрической мощностью 10 МВт, создана в ФГУП «НПП Мотор» (г. Уфа).

Рис. 1. Энергоустановка ГТЭ-10/95
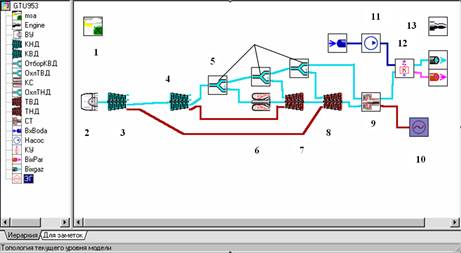
Рис. 2. Схема энергоустановки ГТЭ-10/95 в СИМ,
где 1- внешние условия; 2-входное устройство; 3-КНД; 4 – КВД; 5- отбор газа; 6 – камера сгорания; 7 – ТВД; 8 - ТНД; 9 – свободная турбина; 10 – генератор; 11 – насос; 12- котел-утилизатор; 13 – общие результаты
Получение заданной мощности установки N=10 МВт необходимо при условиях минимума расхода топлива (максимум КПД установки) и минимума температуры газа перед турбиной (максимальный ресурс двигателя).
Результаты расчетов показаны на рис. 3 - 5.
Сравнение полученных статических характеристик с экспериментальными данными подтверждает достаточную (с учетом предъявленных требований) степень адекватности модели. Проводится моделирование динамических характеристик установки при резком изменении нагрузки на электрогенераторе. Используется модель с регулятором для поддержания частоты вращения свободной турбины. Котел-утилизатор при моделировании динамики в схему не включен. Моделирование в СИМ позволило определить закон подачи топлива в камеру сгорания для поддержания постоянной частоты вращения свободной турбины, а значит и электрогенератора.
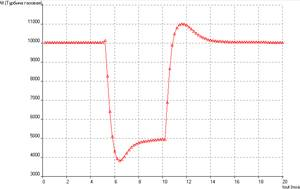
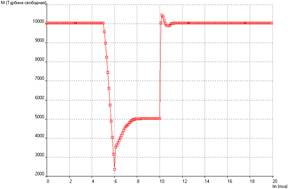
a) б)
Рис. 3. Изменения мощности свободной турбины по времени
а) пропорциональный закон; б) пропорционально-дифференциальный
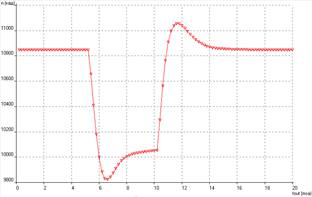
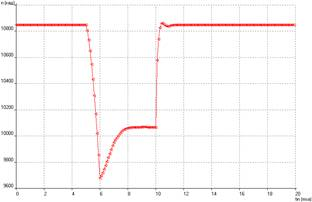
a) б)
Рис. 4. Изменение частоты вращения КВД по времени
а) пропорциональный закон; б) пропорционально-дифференциальный
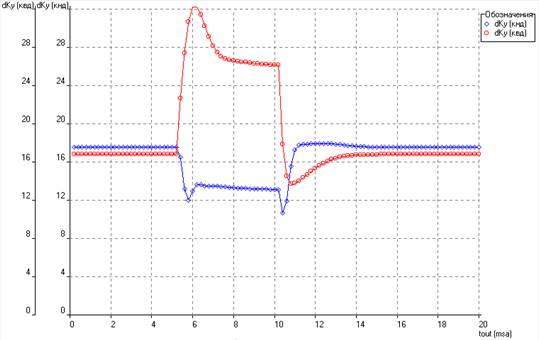
Рис. 6. Изменение запасов устойчивости компрессоров по времени
Таким образом, варьируя параметрами регуляторов (постоянными времени, коэффициентами демпфирования) удалось оптимизировать законы управления и получить необходимое качество переходных процессов (время регулирования, перерегулирование, колебательность и т.п.).
Работа выполнена при финансовой поддержке гранта МД-277.2010.8
Список литературы
1. Теория, расчет и проектирование авиационных двигателей и энергетических установок: Учебник / Под общей ред. В.А. Сосунова, В.М. Чепкина. М.: МАИ, 2003. - 688 с.
2. Кривошеев, И.А. Методы и средства системной разработки сложных объектов на основе имитационного сетевого моделирования и технологии МетаСАПР /И.А. Кривошеев, Д.А. Ахмедзянов и др. Приложение к журналу “Информационные технологии”. – Москва, 2005. – №4. – 32 с.
3. Ахмедзянов, Д.А.Термогазодинамический анализ рабочих процессов ГТД в компьютерной среде DVIGw / Д.А. Ахмедзянов, И.А. Кривошеев и др. Уфа: Изд. Уфимск. гос. авиац. техн. ун-та, 2003. – 162 с.
4. Родионов, А. В. Анализ термодинамических параметров зарубежных малоразмерных газотурбинных установок [Текст] / А. В. Родионов, И. А. Кривошеев // Молодой ученый. – 2009. – №9. – С. 21-24.







