В этой работе метод вариационных итераций (МВИ) применяется для решения волновых уравнений. МВИ обеспечивает последовательность функций, которая сходится к точному решению и способен отменить некоторые из повторных вычислений. Метод очень прост и удобен.
Ключевые слова: дифференциальные уравнения в частных проихводных, метод вариационных итераций, коррекция функционала, начальное приближение, последовательность функции, точное решение
Изучение численных методов решения нелинейных уравнений с частными производными пользуется интенсивный период деятельности в течение последних 50 лет с теоретической и практической точек зрения. Улучшения численных методов, наряду с быстрым прогрессом в области компьютерных технологий, привели к тому, что многие из дифференциальных уравнений в частных производных стало численно анализируемым, вытекающих из инженерных и научных приложений.
Численный методы дополнены методом вариационных итераций (МВИ), разработанный в 1999 г. ученым J. H. He и успешно использовано в работах [2–3] для изучения линейной и нелинейное волновое уравнение, волнообразный уравнение в ограниченных и неограниченных областях. Также было показано многими авторами, что этот метод является надежным и эффективным, более мощным, чем у существующих технологий, таких как метод разложения Адомина [6–7], метод возмущений и т. д. МВИ дает быстро сходящихся последовательных приближений точного решения, если такое решение существует; в противном случае несколько приближений можно использовать для численных целей. Метод эффективно используется в [1–7] и ссылки в ней. Метод возмущений создает вычислительную нагрузку, особенно, когда степень нелинейности увеличивается, а метод разложения Адомина создает сложных алгоритмов, используемых для вычисления полиномов Адомина, которые необходимы для нелинейных задач. ВИМ не имеет каких-либо конкретных требований, таких как линеаризация, малых параметров и т. д. для нелинейных операторов.
Цель этой работы является показать эффективность использования метода вариационных итераций, чтобы установить точные решения.
Постановка задачи. Значительное количество исследовательских работ было направлено на изучение линейные и нелинейные волновые уравнения, волновые уравнения типа в ограниченных (0 < x < L, t > 0) или в неограниченных (–∞ < x < +∞, t > 0) областях, который задается в виде
![]() . (1)
. (1)
Такие волновые уравнения играет важную роль в различных физических проблемах. Исследование волнового уравнения необходимо в различных областях инженерных и научных приложений и огромное количество исследовательских работ было вложено в исследование таких уравнений. Стандартные методы являются разделение метода переменных, метод Даламбера и многие другие. Как сказали выше, этот метод является надежным и эффективные для обработки линейных и нелинейных задач, однородные или неоднородные, и в ограниченной области или неограниченная область. В отличие от других методов, МВИ используется непосредственно без каких-либо требований или ограничительные предположения для нелинейных членов. Еще одним важным преимуществом этого метода является то, что он способен значительно уменьшая размер вычислений, при сохраняя при этом высокую точность численного решения. В дальнейшем мы будем кратко осветить основные моменты метода, в котором детали можно найти в работах [6–7] и ссылки в них.
Алгоритм метода вариационных итераций. Рассмотрим дифференциальное уравнение
Lu + Nu =f(x,t), (2)
где N и L являются линейными и нелинейными операторами над искомой функции u(x,t), а существование функции f(x,t) означает неоднородность этого уравнения. J. H. He предложил метод вариационных итераций, где коррекция функционала для уравнения (2) можно записать в виде
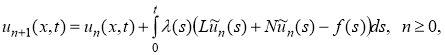 (3)
(3)
где — общий множитель Лагранжа, который сначала может быть определен с помощью оптимально вариационной теории. С выбором нулевого приближения u0 и последовательным приближением un+1(х, t), n ≥ 0 легко получается решения u(х, t), где начальные значения u(х,0) и ut(х,0), как правило, используются для выбора нулевого приближения. Следовательно, решение дается формулой ![]() . В дальнейшем мы будем применять МВИ для некоторых физических моделей, чтобы проиллюстрировать силу метода и установить точные решения для этих моделей.
. В дальнейшем мы будем применять МВИ для некоторых физических моделей, чтобы проиллюстрировать силу метода и установить точные решения для этих моделей.
Пример 1. Сначала рассмотрим самый простой пример. Требуется решить следующую краевую задачу (F = 0, f = 0):
utt= uxx, 0 < x < π, t > 0,
u(0,t) = 0, u(π,t) = 0, t > 0, u(x,0) = 0, ut(x,0) = sin x, 0 ≤ x ≤ π. (4)
Коррекция функционала для заданной уравнение (4) имеет вид
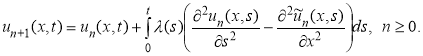 (5)
(5)
Множителя Лагранжа находим из стационарного состояния: 1–′(s) = 0, (s = t) = 0, ′′(s)= 0. Отсюда
= s — t. (6)
Подставляя (6) в (5) имеем итерационную формулу:
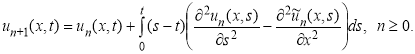 (7)
(7)
Начальное приближение выбираем из начальных условий: u0(x,t) = tsinx. Далее имеем
![]() ;
; ![]() ;
; ![]() ;
;
...; ![]() .
.
Окончательное решение ![]()
Расчеты проверены с помощью Maple 13 [8] и полученные результаты на третьем приближении представлены на рис.1.
Пример 2. Требуется решить следующую краевую задачу с однородным линейным волновым уравнением
utt= uxx — 3u, 0 < x < π, t > 0,
u(0,t) = 0, u(π,t) = 0, t > 0, u(x,0) = sin x, ut(x,0) = 0, 0 ≤ x ≤ π. (8)
Следует отметить, что дополнительный член –3u, добавленный к традиционному волновому уравнению, возникает тогда, когда каждый элемент исследуемого объекта подвергается дополнительной силой, пропорциональной его перемещению.
Как и в предыдущем примере, коррекция функционала для заданной уравнение (8) имеет вид
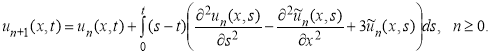 (9)
(9)
Начальное приближение выбираем из начальных условий: u0(x,t) = sinx. Далее имеем
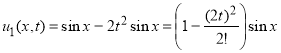 ;
;
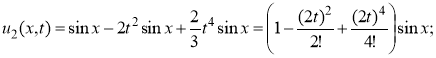
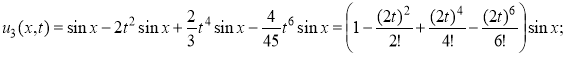
...; 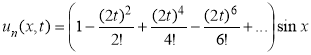 .
.
Окончательное решение ![]()
Пример 3. Требуется решить следующую краевую задачу с неоднородным линейным волновым уравнением
utt= uxx — u +2sinx, 0 < x < π, t > 0,
u(0,t) = 0, u(π,t) = 0, t > 0, u(x,0) = sin x, ut(x,0) = 1, 0 ≤ x ≤ π.
Как и в предыдущем примере, итерационная формула имеет вид
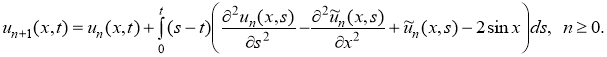
Начальное приближение выбираем из начальных условий: u0(x,t) = t + sinx. Далее имеем
![]() ;
; ![]() ;
;
![]() ;...;
;...; ![]() .
.
Окончательное решение ![]()
Пример 4. Требуется решить следующую краевую задачу с однородным нелинейным волновым уравнением
utt= uxx — u — u3, 0 < x < L, t > 0,
ux(0,t) = 0, ux(L,t) = 0, t > 0, u(x,0) = A [1+cos(2πx/L)], ut(x,0) = 0, 0 ≤ x ≤ L.
Как и в предыдущем примере, итерационная формула имеет вид
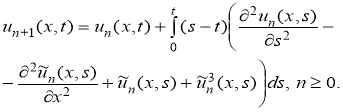
Начальное приближение выбираем из начальных условий вида ![]() . Дальнейшие приближения вычислены с помощью Maple 13 и полученные результаты для L = 1, A = 1.5 на третьем приближении представлены на рис.2. При третьем приближении этот метод дал результат, соответствующие с результатом работы [7], который эта задача была решена с помощью методом разложения Адомиана.
. Дальнейшие приближения вычислены с помощью Maple 13 и полученные результаты для L = 1, A = 1.5 на третьем приближении представлены на рис.2. При третьем приближении этот метод дал результат, соответствующие с результатом работы [7], который эта задача была решена с помощью методом разложения Адомиана.
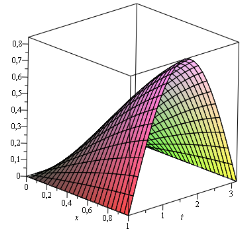
Рис. 1.
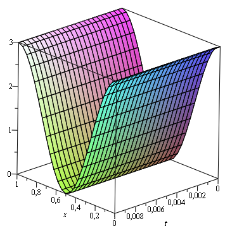
Рис. 2.
Пример 5. Требуется решить следующую краевую задачу с неоднородным нелинейным волновым уравнением
utt= uxx — u — u2 + xt +x2t2, 0 < x < π, t > 0,
u(0,t) = 0, u(π,t) = π·t, t > 0, u(x,0) = 0, ut(x,0) = x, 0 ≤ x ≤ π,
Как и в первом примере, итерационная формула имеет вид
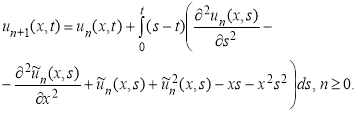
Начальное приближение выбираем из начальных условий вида
Выводы. Результаты расчетов проверены с помощью математического пакета Maple 13 [8]. Очевидно, что МВИ является очень мощным и эффективным методом для нахождения аналитических решений для широких классов нелинейные задачи. Этот метод не требует дискретизация переменные, нет вычисления ошибки округления, не требует малых параметров, которые необходимы методом возмущений, избегает линеаризацию и физически нереалистичные предположения, может преодолеть трудности, возникающие при расчете полиномов Adomian. Этот метод широко распространены по приложениям [1–7].
Литература:
- Abdou, M.A., Soliman A. A. Variational iteration method for Solving Burger’s equations. Journal of Computational and Appl. Math., 2005, 181 (2): 245–251.
- He J. H., Wu X. H. Variational iteration method: New development and applications, Computers and Mathematics with Applications. 2007, 54 (7–8): 881–894.
- He J. H. Variational iteration method — some recent results and new interpretations, Journal of Computational and Applied Mathematics 207(1) (2007) 3–17.
- Wazwaz A. M. The variational iteration method for analytic treatment for linear and nonlinear ODEs. Appl. Math. and Computation, 2009, 212 (1): 120–134.
- Wazwaz A. M. The variational iteration method for solving linear and nonlinear ODEs and scientific models with variable coefficients. Central European Journal of Engineering. 4(1), 2014, 64–71.
- Wazwaz A. M. A First Cours in Integral Equations. Second Edition. Chicago: Saint Xavier University, 2015. — 331 p.
- Wazwaz A. M. Partial Differential Equations and Solitary Waves Theory. Higher Education Press, Beijing and Springer-Verlag Berlin Heidelberg, 2009. — 761 p.
- Алексеев Е. Р., Чеснокова О. В. Решение задач вычислительной математики в пакетах Mathcad, Matlab, Maple (Самоучитель).– М.: НТ Пресс, 2006.– 496 с.







