Термин “задача” широко используется в практике и науке, и понимается исследователями по-разному. Например, это понятие объяснили и определили в логике В.Ф. Берков [1] и Ф.С. Лимантов [2], в психологии Г.А. Балл [3], в эпистемологии У.Р. Рейтман [4], в кибернетике и инженерной технике Э.Крик [5], а в педагогике исследовали С.О. Шатуновский [6], И.М.Фридман и К.К. Джумаев [7] в методике преподавания математики, В.Оконь [8] задачу-вопрос и А.М. Матюшкин [9] со стороны проблемной ситуации.
В этих исследованиях были различные подходы к вопросу о задачах, те или иные исследователи давали свои объяснения, в том числе о субъектах, которые решали задачи.
Г.А.Балл [3], Я.А.Пономарев [10] и К.А. Славская [11] считали, что решение задач невозможно рассматривать без субъекта и условий его работы, а А.В. Брушлинский [12] и А.М. Матюшкин [9] и другие исследовали эту проблему вне зависимости от субъекта.
Задачи играют особенно большую роль в обучении. Поэтому задача и процессы решений задач являются основным объектом исследования дидактики. Задачи, их структуры, проблема, процессы решения являются предметом исследований многих наук: педагогика, психология, физика, общественная наука, техническая наука и другие. Термин “задача” понимается в общем смысле как задача, требующая “решения” и “завершения” и задачи, применяемые в различных областях науки, имеют свою специфику и соответствующие ей своеобразные приемы.
В педагогике, частной дидактике специально рассмотрена структура задач, методология их решения. Здесь особое место занимают исследования Л.М. Фридмана.
Л.М. Фридман понимал задачу как систему с особой структурой и на основе этого анализировал деятельность субъекта. Он также подвергал анализу структуру учебных задач и логико-психологическую деятельность решения задачи, это стало основой общей методологии исследования и типологии задач. Л.М. Фридман подробно исследовал генезис, структуру задач и логико-психологическую основу деятельности по решению задач, итогом его исследований в этой области стала монография, основополагающий труд теории и методологии решения задач. Кроме этого, Фридман специально исследовал основные параметры задач, нормативную деятельность по решению задач и методику решения и опознавания задач. Мы особо ценим подходы, рассмотренные в этом исследовании.
Генезисом задач являются проблемные ситуации. Проблемной ситуацией, моделью является задача. Задача преподносится субъекту в виде схемы на каком-либо языке.
Субъект понимает задачу по-своему и у него появляется интерес переработать и сформулировать задачу. В основном, это является схемой деятельности субъекта и объектом деятельности субъекта.
Хотя задания и задачи, применяемые в жизни и учебной практике, различаются по содержанию и форме, Л.М.Фридман на основе своего исследования выяснил, что эти задачи состоят из сходных между собой элементов. При этом задача рассматривается как высказывание, форма высказывания и система требований и выявляется схема высказываний. Схема общих высказываний выявляется на основе выделения высказываний и формулирования их в виде высказываний в логике. Он считал, что обобщенная модель высказывания по структуре имеет три различных вида.
Всякая задача состоит из условия, требования и оператора. Её структуру можно представить в следующем виде.
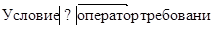
Здесь  есть знак оператора задачи.[7, c. 24]
есть знак оператора задачи.[7, c. 24]
В физическом обучении мы широко используем логическую задачу /качественную задачу/. При решении задач достаточно перечислить примененные законы и написать ответ. Важнейшим требованием к решению физико-логических задач является доказательность изложения. Это требование связано с одним из важнейших требований к научному описанию: результат не должен зависеть от личности исследователя, его вкусов и предпочтений. Поэтому необходимо привести всю цепочку рассуждений.
В физико-логическую задачу используем теорию Л.М.Фридмана.
Первый вид. Задачи на разыскание искомого.
Задача 1. Какое явление называют испарением?
Обобщенную высказывательную модель задачи 1 можно представить в виде следующей структурной модели:
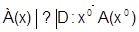
Здесь дана высказывательная форма А(х). Найти такие действия D, которые дают значения х0 переменной х, при которых заданная форма обращается в истинное высказывание А(х0).
Второй вид. Задачи на доказательство или объяснение.
Задача 3. Почему жидкости и газы нагревают снизу?
Задача 4. В сосуд с водой опущен кусок дерева. Изменится ли от этого давление на дно сосуда, если вода из сосуда не выливается?
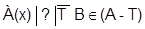
Это такая задача, в которой дано высказывание А, и чтобы найти Т, необходимо применение расширенной теории, содержащей высказывание В.
3. Задачи на преобразование и построение имеют следующую структуру.
Задача 5. Объясните, как происходит нагревание воды в колбе, поставленной на огонь.
Задача 6. Как сообщить двум изолированным проводникам разноимённые заряды, имея стеклянную палочку и кожу?
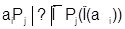
Даны элементы 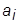 и свойства
и свойства 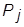 . Найти такую последовательность преобразований, применяя которые к элементам
. Найти такую последовательность преобразований, применяя которые к элементам 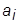 получим объект
получим объект 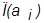 , обладающими всеми свойствами
, обладающими всеми свойствами 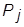 .
.
Ю.Н. Кулюткин [13] первый вид задач называет задачами на распознавание, а третий – задачами на конструирование. Д.Пойа [14] первый вид задач называет задачами на нахождение.
Результаты решения таких задач имеют объективный характер, поскольку они зависят от определяющих характеристик, таких как содержание и форма задач, одновременно они имеют субъективный характер, поскольку зависят от подготовки учащихся, решающих задач и цели учителя, который руководит и направляет деятельность учащихся.
В практике межпредметные связи обнаруживаются связью между содержанием, они также выражаются и методологическими связями. Например, методы, используемые при решении физической количественной задачи, являются методами математической задачи. Методы, применяемые при решении логической или качественной задачи физики, являются приемами умозаключения и являются вполне неопределенными, поскольку зависят от содержания задач и предъявляемых к ним требований.
Теория, выдвигаемая Л.М.Фридманом, дает возможность направлять определенным образом проблему решения задачи, ее цели и конкретные действие по решению задачи.
Благодаря ознакомлению учащихся вышесказанных трех общих типов задач, применяемых на каждом занятии независимо от видов учебной деятельности, дается возможность достичь методологического единства решения проблем, сформулировать цели решения задач и предвидеть ее результаты. Это дает учителю возможности дифференцировать задач по уровню. Трудность в применении этой теории является аспектом логики, а их решение повышает умственный потенциал и учащихся, и учителей. В результате решения учебных задач ученики усваивают методику решения задач, возникающих в жизненной ситуации. Таким образом, учащиеся учатся решать жизненные проблемы посредством учебной деятельности.
Библиографический список
1. Берков, В.Ф. Вопрос как форма мысли. Минск. Изд-во БГУ, 1972.
2. Лимантов, Ф.С. О природе вопроса. В.сб.: Вопрос. Мнение. Человек. Л., изд. ЛГПИ им. А.И.Герцена, 1971.
3. Балл, Г.А. О психологическом содержании понятия ”задача”. Вопросы психологии. 1970. ¹6
4. Рейтман, У.Р. Познание и мышление. М., Мир. 1968.
5. Крик, Э. Введение в инженерное дело. М., Энергия. 1970.
6. Шатуновский, С.О. Геометрические задачи и их решение с помощью циркуля и линейки. В кн.: Адлер А. Теория геометрических построений. М., Учпедгиз, 1940.
7. Фридман, И.М. Логико-психологический анализ школьных учебных задач. Изд-во Педагогика. 1977.
8. Оконь, В. Основы проблемного обучения. М., Просвещение. 1968.
9. Матюшкин, А.М. Основные психологические модели проблемных ситуаций. В сб.: Основные подходы к моделированию психики и эвристическому программированию. М., 1968.
10. Пономарев, Я.А. Психология творческого мышления. М., Изд-во АПН РСФСР. 1960.
11. Славская, К.А. Мысль в действии. М., Политиздат. 1968.
12. Брушлинский, А.В. О некоторых методах моделирования в психологии. В сб.: Методологические и теоретические проблемы психологии. М., Наука. 1969.
13. Кулюткин, Ю.Н. Эвристические методы в структуре решений. М., Педагогика. 1970.
14. Пойа, Д. Математика и правдоподобные рассуждения. М., ИЛ. 1957.
15. Отгонбаяр, М. Логик. Уланбаатар. 2004.







