Предельная эффективность ипараметрический анализ взадачах линейного программирования
Селюкова Светлана Александровна, старший преподаватель;
Селюкова Галина Петровна, кандидат сельскохозяйственных наук, доцент
Государственный аграрный университет Северного Зауралья (г. Тюмень)
Решение задачи линейного программирования в Excel позволяет получить оптимальное решение и попутно создается отчет по устойчивости, который содержит двойственные оценки полученного решения. Позволяет ответить на вопросы: что, если производить то, что не рекомендуется, как изменится решение, если изменится количество ресурсов или планы хозяйства и в каких пределах.
Важная характеристика — теневая цена, которая позволяет оценить эффективность ресурсов и рассчитать предельную эффективность для каждого ресурса.
Оптимальное решение должно помочь руководителю хозяйства выбрать правильное решение в конкретной ситуации и в меняющихся условиях. Наряду с анализом двойственных оценок и допустимых пределов изменения коэффициентов целевой функции и объемов ограничений, можно провести параметрический анализ по одному или нескольким параметрам. Параметрический анализ дает пищу для размышления руководителю и позволяет учесть специфические условия работы.
Рассмотрим это на простом примере. Задача распределения ресурсов может быть описана системой неравенств и уравнений (рис. 1). Необходимо определить план производства продукции 5 видов. Имеется четыре вида ресурсов. Известны нормы расхода каждого ресурса, прибыль от единицы продукции и количество каждого ресурса. Критерием оптимальности является максимум прибыли.
Решим задачу линейного программирования в Excel и создадим отчет по устойчивости [2, с. 176; 3, с. 373].
По оптимальному решению предлагается производить только вторую (20 единиц) и четвертую (12 единиц) продукцию (рис. 1). При этом полностью будут использованы трудовые ресурсы и финансы. Сырье и механизированный труд используются не полностью. Прибыль будет максимальной и составит 5520 денежных единиц.
Нормированная стоимость показывает, что если производить единицу продукции, то прибыль снизится: если первой продукции, то на 47 ден. ед., третьей — на 27 ден. ед., пятой — на 107 ден. ед. (рис. 2). То есть самой затратной при таких условиях является пятая продукция.
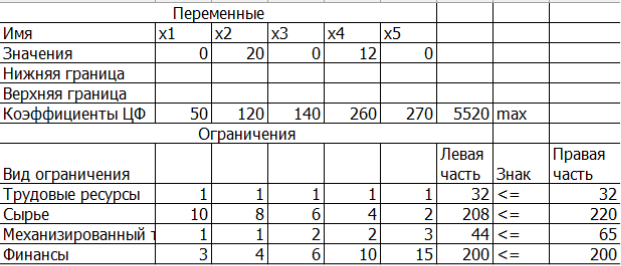
Рис. 1. Оптимальное решение
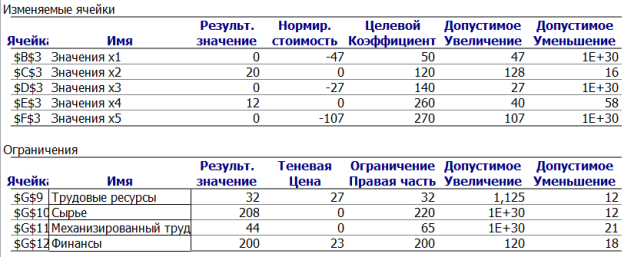
Рис. 2. Отчет по устойчивости
Теневая цена показывает, что если увеличить (уменьшить трудовые ресурсы на единицу, то прибыл увеличится (уменьшится) на 27 единиц, а если увеличить (уменьшить) финансы на единицу, то прибыль увеличится (уменьшится) на 23 единицы. При этом возможные пределы изменения трудовых ресурсов составляют от 20 до 33 единиц, а финансов от 182 до 320 (рис. 2).
На основе данных отчета по устойчивости определим предельную эффективность финансов [1, с. 48]. Для этого решим задачу при количестве финансов 321, получим значение теневой цены равное 2, а пределы финансов от 320 до 325. Решение при 326 даст новые результаты: теневая цена 0, а пределы от 325 и до бесконечности. Предел наименьшей эффективности финансов найден. Найдем наибольшую эффективность этого ресурса. Для этого решим задачу при количестве финансов 319, 181 и 109 (табл. 1.)
Таблица 1
Результаты расчета предельной эффективности финансов
|
Количество финансов |
Теневая цена |
Минимальная граница |
Максимальная граница |
|
326 |
0 |
325 |
∞ |
|
321 |
2 |
320 |
325 |
|
319 |
23 |
182 |
320 |
|
181 |
25 |
110 |
182 |
|
109 |
30 |
0 |
110 |
Анализ результатов расчета предельной эффективности финансов показывает, что при заданных условиях максимальной эффективности финансы достигают при их количестве от 0 до 109. Если финансы превышают 325 денежных единиц, то они становятся неэффективными.
Определив предельную эффективность всех ресурсов, можно принять правильное решение по изменению объемов наиболее эффективных ресурсов в зависимости от сложившейся ситуации.
Для получения вариантов развития производства продукции проведем параметрический анализ по финансам. Отчет по устойчивости свидетельствует, что решение останется оптимальным, если количество финансов будет находиться в пределах от 182 до 320 денежных единиц.
Параметрический анализ проведем при количестве финансов от 100 до 350 денежных единиц с шагом 50. Для этого решим задачу с различными значениями финансов и результаты оформим в таблице 2.
Значения финансов 200, 250 и 300 находятся в допустимых пределах, поэтому мы видим, что план производства такой, как получили по оптимальному решению, то есть предлагается производить вторую и четвертую продукцию. Значения 100 и 150 меньше нижней границы допустимых пределов и план производства в первом случае представлен только второй продукцией. Значения выше верхнего предела 350 вновь дает новый план производства, а именно четвертую и пятую продукцию. То есть анализ планов производства показывает, что развитие может идти по разным направлениям в зависимости от количества финансов: от второй, ко второй и четвертой продукции и к четвертой и пятой.
Таблица 2
Параметрический анализ по финансам
|
Результаты решения |
Количество финансов, ден. ед. |
|||||
|
100 |
150 |
200 |
250 |
300 |
350 |
|
|
Переменные |
||||||
|
Х1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Х2 |
25 |
25 |
20 |
12 |
3 |
0 |
|
Х3 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Х4 |
0 |
5 |
12 |
20 |
29 |
31 |
|
Х5 |
0 |
0 |
0 |
0 |
0 |
1 |
|
Целевая функция |
||||||
|
3000 |
4300 |
5520 |
6687 |
7853 |
8330 |
|
|
Расход ресурсов |
||||||
|
Трудовые |
25 |
30 |
32 |
32 |
32 |
32 |
|
Сырье |
200 |
220 |
208 |
175 |
141 |
126 |
|
Мех. труд |
25 |
35 |
44 |
52 |
61 |
65 |
|
Финансы |
100 |
150 |
200 |
250 |
300 |
325 |
При увеличении количества финансов увеличивается и максимально возможная прибыль, но темпы ее увеличения снижаются с 1300 до 477 денежных единиц. Поэтому однозначно сказать, какой вариант лучше, нельзя. Это зависит от комплекса факторов важных для хозяйства.
Анализ расхода ресурсов показывает, что полностью используются финансы во всех случаях, кроме последнего. При количестве финансов 350 они не могут быть освоены из-за полного расхода трудовых ресурсов и механизированного труда.
Трудовые ресурсы не полностью задействованы при количестве финансов 100 и 150, а механизированный труд не полностью используется во всех вариантах, кроме последнего, хотя его использование постоянно увеличивается.
Сырье полностью используется только при количестве финансов 150 денежных единиц, начиная со следующего варианта расход сырья снижается от 208 до 146 единиц.
В результате по этим данным можно определить наиболее подходящий план производства, обеспечивающий необходимую прибыль. Принять меры по увеличению некоторых ресурсов, а при необходимости их использованию на другие цели.
Литература:
- Савиных В. Н. Математическое моделирование производственного и финансового менеджмента [Текст]: учеб. пособие / В. Н. Савиных. — Новосибирск: СГГА, 2007. — 219 с.
- Гармаш А. Н., Орлова И. В. Математические методы в управлении: Учебное пособие. — М.: Вузовский учебник: ИНФРА-М, 2014. — 272 — c.
- Селюкова С. А., Селюкова Г. П. Целочисленное решение задач линейного программирования методом ветвей и границ с помощью Excel // Молодой ученый. — 2016. — № 12 (116). — С. 372–374.







