Моделирование искрового плазменного спекания: цели, задачи, проблемы и пути их решения



Искровое плазменное спекание (ИПС) является одной из самых перспективных технологий синтеза новых порошковых материалов с уникальными свойствами. Однако, широкая номенклатура спекаемых материалов и сложность процесса ИПС сильно затрудняют назначение рациональных технологических режимов, необходимых для получения нужных свойств готового материала. При этом, технологические эксперименты очень дороги и трудоемки. Для сокращения количества экспериментов необходимо выявить зависимости свойств спекаемых материалов от режимов и условий процесса ИПС. Для решения этой сложной, но очень важной задачи, требуется комплексный подход, объединяющий экспериментальные исследования, численное моделирование и теорию спекания порошковых материалов.

Ключевые слова: искровое плазменное спекание; численное моделирование, метод конечных элементов, теория спекания

Spark plasma sintering (SPS) is one of the most promising technologies for the synthesis of new powder materials with unique properties. However, for a wide range of sintered materials and the complexity of the process of SPS are very difficult to assign to rational technological modes needed to obtain the desired properties of the finished material. At the same time, the technological experiments are very expensive and time consuming. To reduce the number of experiments, it is necessary to identify the dependence of the properties of sintered materials from the modes and conditions of the SPS process. To resolve this complicated but important task, it is required a comprehensive approach that combines experimental studies, numerical simulation and the theory of sintering of powder materials.

Key words: spark plasma sintering, numerical simulation, finite element method, theory of sintering.

В данной работе представлен анализ технологического процесса и краткая характеристика основных теоретических моделей ИПС. Рассмотрен опыт применения численного моделирования МКЭ для исследования ИПС. Сформулированы цели и задачи численного моделирования данного технологического процесса. Обозначены основные недостатки и ограничения известных методик моделирования. Предложены варианты развития методик моделирования ИПС на основе комплексного подхода, объединяющего теоретические и экспериментальные исследования с численным моделированием и постановкой виртуальных экспериментов.

Одной из основных задач материаловедения является установление закономерностей зависимости свойств материалов от их микроструктуры и элементного состава. В свою очередь с этой задачей неразрывно связана важнейшая задача технологии материалов — получение требуемых свойств материалов при их синтезе, что достигается образованием необходимой микроструктуры и обеспечением нужного элементного состава. Данная задача, в настоящее время, приобрела особую актуальность в связи с быстрым развитием материаловедения и появлением новых технологий синтеза материалов с уникальными свойствами. Одной из таких технологий и является искровое плазменное спекание (ИПС) (англ. Spark Plasma Sintering (SPS) илиField Assisted Sintering Technology (FAST)).

В процессе ИПС порошковая засыпка нагревается посредством пропускания через систему импульсного постоянного тока большой силы, и подвергается одноосному механическому давлению. ИПС существенно сокращает время синтеза образцов и улучшает качество спеченного материала, так как позволяет свести к минимуму рост зерен и сохранить нано- и суб- микроструктуры в нанодисперсных порошковых материалах [1- 3].

ИПС обладает очень широкими возможностями для спекания различных порошковых материалов и большой гибкостью технологического процесса, результат которого зависит от большого количества различных параметров. Это существенно затрудняет назначение рациональных технологических режимов. Кроме того, недостаток объективных знаний о процессах, протекающих в порошковой засыпке при ИПС, ограничивает уровень теоретического описания данной технологии, и, соответственно, предсказательные способности существующих теорий. Эмпирический подход продолжает оставаться основным методом исследования процессов ИПС и разработки технологических процессов создания материалов. Однако, высокая стоимость и большая трудоемкость подобных экспериментов определяют необходимость применения методов численных моделирования и дальнейшего развития теоретического описания ИПС.

Анализ технологического процесса искрового плазменного спекания. Технологический процесс ИПС порошковых материалов можно представить, как систему, состоящую из совокупности параметров (рис. 1): входных параметров -технологических режимов и исходных условий; контролируемых параметров процесса; выходных параметров -свойств материалов спечённого образца. Для практических целей спекания материалов с необходимыми свойствами наиболее важно знание закономерностей влияния технологических режимов на параметры качества материала спеченного образца. Для моделирования и теоретического исследования ИПС важно знать все закономерности взаимосвязей параметров технологического процесса.

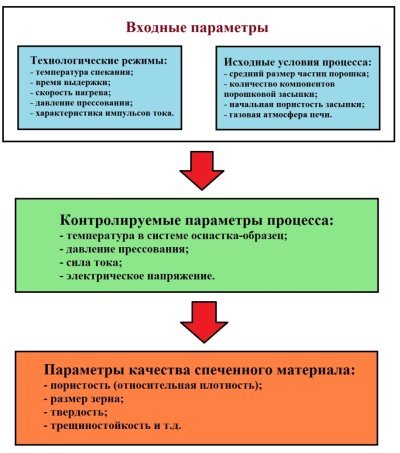
Рис. 1. Схема системы технологического процесса ИПС

Теоретическое описание ИПС. В настоящее время существует несколько вариантов теоретического описания процесса ИПС. Наибольшее распространение получили теория Олевского и, так называемый, закон Абюфа (англ. Abouaf law).

Теория спекания Олевского.Основными факторами спекания, обеспечивающими массоперенос являются: деформация по степенному закону ползучести и зернограничная диффузия [4]. Деформация порошковой засыпки выражена в определяющем уравнении, которое связывает внешнее давление σ_ij с компонентами тензора скоростей деформаций ε'_ij нелинейно-вязкими определяющими соотношением [5]:

, (1)

где: W–есть эквивалентная скорость деформации и σ(W) — эквивалентное напряжение; φ и ψ — нормированные сдвиговая и объемная вязкости; δ_ij — символ Кронекера; ε'_ij- тензор скорости деформации; e'_Cr — первый инвариант тензора скорости деформации по степенному закону ползучести; P_L — эффективное давление спекания.

Эквивалентная скорость деформации W зависит от пористости и инвариантов тензора скорости деформации:

, (2)

где: θ — пористость, γ' — второй инвариант девиатора скорости деформации.

Эквивалентное напряжение выражается следующим образом:

, (3)

где A и m — параметры закона ползучести. А определяется как:

, (4)

где: Ã — предэкспоненциальный множитель; Т — температура; m — показатель степени в законе ползучести; ΔH_SD — энергия активации самодиффузии; R — универсальная газовая постоянная.

В определяющем уравнении (1) два параметра φ и ψ являются функциями пористости, и выражаются, в соответствии с реологической моделью Скорохода, следующим образом:

(5)

Эффективное давление спекания P_L функционально зависит от пористости и от размеров частиц спекаемого порошка:

, (6)

где: θ — пористость, α — поверхностное натяжение, G — средний радиус частицы порошка (на ранних стадиях спекания) и средний размер зерна (на поздних стадиях спекания).

Для вычисления скорости изменения пористости используется уравнение закона сохранения массы порошковой засыпки:

, (7)

где: e' — общая скорость деформации (усадки) порошковой засыпки; θ' — скорость изменения пористости.

Общая скорость деформации e' является суммой двух скоростей деформации, обусловленных ползучестью (e'_Cr) и зернограничной диффузией (e'_gb) [6]:

(8)

В свою очередь, e'_gbявляется суммой трех компонентов, которые представляют вклад установившейся электромиграции в общую скорость деформации, вклад от сил поверхностного натяжения и вклад от внешнего механического давления.

Для вычисления среднего размера частицы порошка (на ранних стадиях спекания) и среднего размер зерна (на поздних стадиях спекания), Олевским было предложено следующее уравнение:

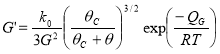, (9)

где: G' — скорость роста частицы порошка или; k₀ — константа, характеризующая свойства материала; Q_G — энергия активации роста зерна; θ_C- критическое значение пористости для перехода от открытых пор к закрытым.

Все параметры, входящие в уравнения (1, 2, 4, 6, 9), определяются экспериментально или берутся из литературных источников.

Закон Абюфа.Основное определяющее уравнение связывает тензор механических напряжений, вызванных внешним механическим давлением, с тензором скорости деформаций порошковой засыпки (деформация соответствует степенному закону ползучести) [8]:

, (10)

где: σ — механическое напряжение, вызванное внешним давлением; K(T) — консистенция материала в плотном состоянии; T — температура; - эквивалентная скорость деформации по степенному закону ползучести; ε' — тензор скорости деформаций; m — параметр степенного закона ползучести (характеристика материала); e' — первый инвариант тензора скорости деформации; c — функция, зависящая от пористости, и связанная с напряжениями сдвига и изменением формы порошковой засыпки в процессе спекания; f — функция, зависящая от пористости, и связанная с гидростатическим давлением и изменением объема порошковой засыпки.

Функции c и fрассчитываются на основе экспериментальных данных по спеканию образцов из данного материала методом горячего изостатического прессования следующим образом:

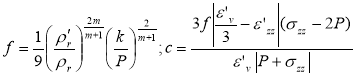, (11)

где: ρ_{r —} относительная плотность (измеряется экспериментально); ρ'_{r —} скорость изменения относительной плотности (измеряется экспериментально); k — коэффициент, функционально зависящий от температуры; P — изостатическое давление прессования; ε'_{v —} первый инвариант тензора скорости деформаций; ε'_{zz —} вертикальная компонента тензора скорости деформаций; σ_{zz —} вертикальная компонента тензора напряжений (рассчитывается исходя из условий эксперимента).

Численное моделирования ИПС. Так как процесс ИПС происходит при высокой температуре, вызванной протеканием импульсного электрического тока, то, в обоих теориях, расчет температуры порошковой засыпки производится по классическим уравнениям, описывающим Джоулев нагрев, теплопроводность и тепловое излучение.

Рассмотренные теории дают две системы уравнений, решая которые, можно рассчитать плотность спекаемого образца, скорость уплотнения, напряжения и деформации в образце, а также температуру и плотность тока. Дополнительно, пользуясь уравнением (10), можно рассчитывать размер зерна и скорость роста зерна.

Аналитические решения этих уравнений позволяют определять только средние значения пористости, размера зерна и температуры. Более важной информацией является распределение значений данных параметров по объёму спекаемого образца. Поэтому, при моделировании процессов ИПС используются методы численного решения рассмотренных систем уравнений для геометрических объемов образца, или системы оснастка — образец. В качестве метода решения, в подавляющем большинстве случаев, метод конечных элементов (МКЭ).

Цели и задачи численного моделирования ИПС

Целями численного моделирования ИПС являются:

1) проведение виртуальных экспериментов для сокращения количества технологических экспериментов при разработке техпроцессов спекания материалов и изделий сложной формы;

2) предсказание свойств спеченных материалов и выявление зависимости свойств от технологических режимов и начальных условий.

Для достижения данных целей необходимо решение основной задачи — разработать методику численного моделирования, которая будет учитывать взаимосвязи всех основных параметров процесса ИПС (рис. 1) и адекватно моделировать изменение микроструктуры спекаемого образца в течении процесса спекания, что позволит производить не только качественную оценку спекания, но и количественно рассчитывать параметры процесса и предсказывать, с достаточной точностью, свойства спеченных материалов.

Применение численного моделирования ИПС. На данный момент, опубликовано некоторое количество работ, выполненных разными исследовательскими группами, которые использовали рассмотренные теории для моделирования МКЭ процесса ИПС. В большинстве из них была применена теория Олевского. Основными результатами стали модели ИПС образцов из меди и оксида алюминия, в которых были получены распределения пористости по объему спекаемого образца и изменение пористости (относительной плотности) в процессе спекания (рис. 2, а). В работах, где анализ МКЭ производился на основе уравнений Олевского, были получены данные о распределении размеров зерна по объему образца и изменение размеров зерна во времени (рис. 2, б). Наиболее полное описание применения закона Абюфа для моделирования ИПС дано в работе [8], где была разработана и протестирована сложная модель процесса ИПС, которая учитывает контактное сопротивление и трение, но не учитывает вклад импульсного тока в кинетику уплотнения порошковой засыпки. В результате, были получены данные о распределении и изменении относительной пористости в сечении спекаемого образца и проведено сравнение результатов моделирования с экспериментальными данными (рис. 3).

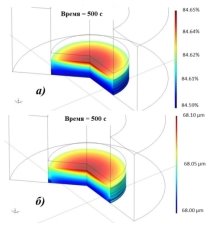
Рис. 2. Модель распределение относительной плотности (а) и размеров зерна (б) по объему образца из медного порошка в процессе ИПС [9]

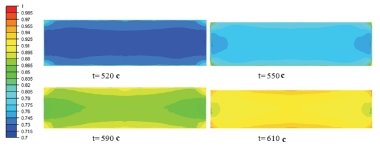
Рис. 3. Модель распределения относительной плотности в сечении образца из материала Инконель (англ. Inconel) в процессе ИПС [8]

Моделирование процесса ИПС, описанное в работах [6-11],имеет ряд допущений и ограничений. Большинство параметров, характеризующих свойства материала порошка было принято константами, хотя они функционально зависят от температуры и пористости. Порошковая засыпка, с самого начала спекания, рассматривается как твердое пористое тело, но в начальный момент времени она является дисперсной системой. Допущение об образце как твердом пористом теле не позволяет учитывать в модели начальные условия спекания: изначальный размер частиц порошка и степень предварительного прессовая засыпки. Данное допущение обуславливает тот факт, что нагрев реальной порошковой засыпки сильно отличается по всем своим параметрам от нагрева образца в модели.

Следующим важным ограничением данных моделей является отсутствие учета характеристик импульсного тока, то есть длительность импульсов и пауз, и их последовательность.

Отдельно необходимо отметить, что в рассмотренных работах не изложена методика моделирования процесса ИПС с помощью МКЭ, а это значительно затрудняет применение теоретических описаний ИПС в исследовательской практике.

Возможные направления развития теоретических исследований ИПС. Рассмотренные теоретические модели позволяют определять, с помощью моделирования МКЭ, пористость спеченных компактов и размер зерна. Что позволяет, с большой погрешностью, судить о свойствах получаемых материалов (твёрдость, трещиностойкость и др.).

Задача о более точном предсказании свойств материалов и назначении рациональных режимов ИПС имеет два возможных варианта решения:

1) теоретический, основанный на физике рассматриваемого процесса;

2) эмпирический, основанный на анализе экспериментальных данных.

Теоретический вариант решения представляет собой математическое описание процесса на трёх уровнях масштаба (микро-, мезо-, макро-), причем, в их взаимосвязи перехода от микро- к макроуровню.

Микроуровень — атомно-молекулярный. На данном уровне необходимо моделировать диффузию атомов, миграцию вакансий и движения дислокаций (в том числе, вызванные электромиграцией, или "электронным ветром" [12]), а также фазовые переходы и химические реакции.

Мезоуровень — моделирование на уровне отдельных частиц порошка. Здесь необходимо учитывать вязкое течение материала, испарение вакансий, напряжения, вызванные механическим давлением, электричеством и кривизной поверхности порошинок и т.д. Здесь появляется связь напряжения и деформации.

Макроуровень — это порошковая засыпка и ее взаимодействие с пресс-формой и другими элементами ИПС системы. Описание макроуровня должно строится на реологии, теплофизике дисперсных систем, протекании тока через дисперсную среду из твёрдых частиц, и, конечно, на известных теориях спекания ИПС.

Создание данной теоретической модели должно не только позволить эффективно решать технологические проблемы ИПС, но и способствовать развитию электроимпульсного спекания и созданию новых технологий синтеза материалов за счёт глубокого понимания физики спекания.

Эмпирический вариантзаключается в систематизации и статистической обработке массива экспериментальных данных, полученных различными исследовательскими группами, с целью выявления зависимостей свойств спеченных материалов от параметров процесса ИПС, режимов и исходных условий. При этом, получаемые взаимосвязи между параметрами процессов не отражают их физической сути. Примером применения такого подхода является методика расчёта режимов резания, которая не затрагивает физической сути резания и является результатом статистической обработки большого массива экспериментальных данных.

Для достижения целей численного моделирования ИПС, в виду большой сложности процесса, наиболее рациональным решением будет разработка методики моделирования, объединяющей оба варианта: теоретический и эмпирический. Взаимосвязи параметров процесса ИПС, режимов и исходных условий, выявленные с помощью эмпирического подхода, предполагается использовать для рационального планирования виртуальных экспериментов, адекватного определения исходных условий, калибровки моделей и оценки адекватности результатов моделирования.

Выводы. На основе анализа основных теоретических разработок и их применения при численном моделировании, были сформулированы цели и задачи моделирования ИПС. Рассмотрены основные недостатки и ограничения существующих подходов к моделированию МКЭ данной технологии спекания. Предложено решение задач моделирования на основе комплексного подхода, объединяющего теоретические модели, методы численного моделирования и статистическую обработку экспериментальных данных. Применение данного подхода предлагается для достижения следующих целей: выявления закономерностей зависимости свойств спекаемых материалов от режимов и условий процесса ИПС, рационального назначения технологических режимов, предсказания свойств синтезируемых материалов, поиска наиболее эффективных направлений исследований процессов ИПС, уменьшения количества технологических экспериментов (исключая заведомо неэффективные). Все это, в комплексе, должно способствовать удешевлению технологии ИПС уже на этапе экспериментальных исследований и ускорить её выход на промышленный уровень.

Литература:

1. Suárez M., Fernández A., Menéndez J.L., Torrecillas R., Kessel H. U., Hennicke J., Kirchner R., Kessel T. Challenges and Opportunities for Spark Plasma Sintering: A Key Technology for a New Generation of Materials / Sintering Applications. Edited by Burcu Ertuğ, ISBN 978-953-51-0974-7, 350 pages, Publisher: InTech, Chapters published February 06, 2013 under CC BY 3.0 license.
2. Orru R., Licheri R., Mario Locci A., Cincotti A., Cao G. Consolidation/synthesis of materials by electric current activated/assisted sintering / R. Orru, R. Licheri, A. Mario Locci, A. Cincotti, G. Cao // Materials Science and Engineering R 63 (2009) 127–287 p.
3. Guillon O., Gonzalez-Julian J., Dargatz B., Kessel T., Schierning G., Rathel J., Herrmann M. Field-Assisted Sintering Technology/ Spark Plasma Sintering: Mechanisms, Materials, and Technology Developments / ADVANCED ENGINEERING MATERIALS 2014, 16, No. 7, p. 830-849.
4. Olevsky E. Theory of sintering: from discrete to continuum / E. Olevsky // Materials Science and Engineering, R23 (1998) 41–100 p.
5. Григорьев Е.Г., Калин Б.А. Электроимпульсная технология формирования материалов из порошков: Учебное пособие / Е.Г. Григорьев, Б.А. Калин // М.: МИФИ, 2008. — 152 с.
6. Olevsky E., Froyen L. Constitutive modeling of spark-plasma sintering of conductive materials / E. Olevsky, L. Froyen // ScriptaMaterialia 55 (2006) 1175–1178 p.
7. E. Olevsky, V. Tikare, and T. Garino, Multi-scale modeling of sintering — A Review, J. Amer. Ceram. Soc., 89 (6),1914-1922 (2006)
8. Mondalek P. Numerical modeling of the spark plasma sintering process / Doctoral thesis. MINES ParisTech, 2012. 235 p.
9. Wei Li. Constitutive Modeling and Simulation of Spark Plasma Sintering with Applications to Fabrication of Functionally Structured Mono-Carbides / Ph. D. thesis. University of California, San Diego, 2013. 271 p.
10. OlevskyE. A. et al. Fundamental Aspects of Spark Plasma Sintering: II. Finite Element Analysis of Scalability / E. A. Olevsky, C. Garcia-Cardona, W. L. Bradbury, C. D. Haines, D. G. Martin, D. Kapoor // J. Am. Ceram. Soc., 95 [8] 2414–2422 (2012).
11. Maniere C. et al. Spark plasma sintering and finite element method: from the identification of the sintering parameters of a submicronic a-alumina powder to the development of complex shapes / C.Maniere, L. Durand, A. Weibel, C.Estournes // ActaMaterialia 102 (2016) 169 — 175 p.
12. Гегузин Я.Е. Физика спекания. — 2-е изд., перераб. и доп. / Я.Е. Гегузин // М.: Наука. Главная редакция физико-математической литературы, 1984. — 312 с.