В наиболее перспективных установках предполагается использование в качестве горючего тритий –не существующий в природе, то возникает проблема обеспечения термоядерных установок тритиевым топливом. Основное направление решения этой проблемы — использование самого термоядерного реактора для наработки трития: нейтроны, получаемые в реакции сгорания трития, предполагается направлять на некоторый элемент (например, литий-6), который в ходе ядерной реакции с нейтронами будет превращаться в тритий [1]. После извлечения из системы генерации (бридерного бланкета), концентрирования и очистки, тритий будет поступать в термоядерный реактор в качестве топлива.
Материал размножителя (бридера) должен обеспечить съем энергии термоядерного синтеза, генерацию трития и эффективное его извлечение для последующей очистки и трансформации в реакторное топливо. Рабочее вещество должно обладать высокой температурной, радиационной, химической и механической стойкостью. Бридерный материал должен обеспечивать возможность количественное извлечение трития при сравнительно низких температурах. Дегазация любого твёрдого тела происходит за счёт диффузионных процессов и зависит от таких факторов, как плотность материала, степень его дефектности, размеры и характер границ зёрен, общая пористость, соотношение открытой и закрытой пористости, площадь открытой поверхности и т. п. В свою очередь эти параметры зависят от условий приготовление гранул (пэбблов): давления прессования, температуры и времени термического отжига [2–5].
Предложенное в настоящей работе математическое и программное обеспечение реакторных экспериментов позволило интерпретировать результаты экспериментов по изучению выделения трития, непрерывно генерируемого в результате ядерной реакции лития-6 с тепловыми нейтронами при наличии переменных термических воздействиях на исследуемый материал. Как было описано в работах [5–8], проведены исследования генерации и выделения трития в литиевой керамике Li2TiO3 (Li2TiO3 + 5 % mol TiO2) с 96 %-ным обогащением по изотопу литий-6 в процессе длительного (5350 ч, 15 кампаний, длительность эксперимента около двух лет) облучения тепловыми нейтронами в реакторе ВВР-К. При этом степень выгорания лития составила 23 %. В ходе эксперимента автоматически и непрерывно измеряли температуру образца и поток трития, выделяющийся из титаната лития.
Таким образом, предложенное в настоящей работе математическое, математическое и программное обеспечение реакторных экспериментов позволило интерпретировать результаты экспериментов по изучению выделения трития, непрерывно генерируемого в результате ядерной реакции лития-6 с тепловыми нейтронами при наличии переменных термических воздействиях на исследуемый материал. Впервые получены данные по выделению трития в условиях его генерации из керамики на базе метатитаната лития, до высокой степени (95 %) обогащённой изотопом 6Li и при высоких степенях выгорания трития. Обнаружено, что процесс выделения трития в основном контролируется объемной диффузией трития, хотя определённую роль играет захват лития точечными дефектами и реакция молизации трития на поверхности материала. Рассчитаны основные параметры газовыделения, необходимые для оценки пригодности пэбблов из титаната лития для использования их в тритиевых бридерах: доля газовыделения, удержание трития в материале, время удержания, энергии активации термодесорбции НТ и объёмной диффузии Т+, а также соответствующие им предъэкспоненциальные (частотные) множители. Показано, что в течение первых трёх месяцев реакторного облучения литиевой керамики, коэффициент диффузии трития увеличивается за счёт уменьшения энергии активации диффузии. Обнаруженный эффект объяснён уменьшением концентрации ионов лития в узлах кристаллической решётки, выступающих как дополнительные диффузионные барьеры. Низкие значения степеней удержания и времён удержания, позволяющие практически полностью обезгаживать пэбблы при сравнительно умеренных температурах, хорошая радиационная, химическая и механическая стойкость, позволяет нам рекомендовать керамику на основе метатитаната лития в качестве бридерного материала для установок управляемого термоядерного синтеза.
Ступенчатый нагрев
Рассмотрим изменение потока газа из сферы при ступенчатом (резком) изменении температуры образца.
В сфере непрерывно и равномерно генерируется стабильный (или долгоживущий) газ. Образец в течение времени t1 выдерживается при температуре Т1. Затем температура образца резко поднимается от значения Т1 до значения T2 и выдерживается в течение времениt2, и т. д. Поскольку при нагреве от Т1 до Т2 коэффициент диффузии изменяется от величины D1до величины D2, то поток газа тоже резко увеличивается (Здесь Т1>Т2, а D1
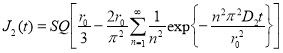 (1)
(1)
и «старые» молекулы, рождённые при температуре Т1, не успевшие выделиться за время 1-го периода t1 (их диффузия управлялась коэффициентом диффузии D1), но при температуре Т2 активно покидающие сферу (их диффузия теперь управляется коэффициентом диффузии D2). Поток молекул этого типа из сферы:
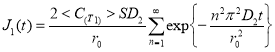 (2)
(2)
где под
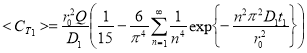 (3)
(3)
Если время выдержки t1 при температуре Т1 достаточно велико, чтобы установилось стационарное состояние диффузии, то
![]() , (4)
, (4)
что значительно упрощает расчёты.
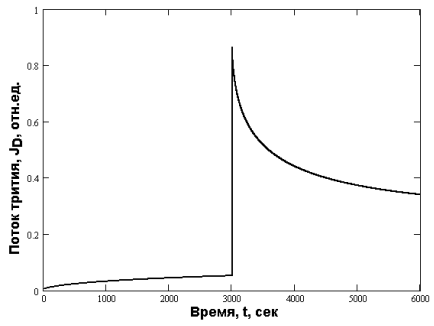
Рис. 1. Изменение потока трития, непрерывно генерируемого в сфере, от времени при ступенчатом изменении коэффициента диффузии (ступенчатый нагрев, D1= 10–9 см2/сек,D2= 10–8 см2/сек,r0=0,1 см)
Связь между коэффициентами диффузии D1 и D2 осуществляется по закону Аррениуса:
![]() (5)
(5)
где D0– предъэкспоненциальный (частотный) множитель [см2/сек], ED– энергия активации диффузии [Дж/моль], R = 8,3144 [Дж/(мольК)]– газовая постоянная; T — температура [градусы Кельвина].
Итак:
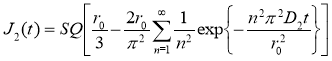
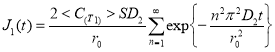
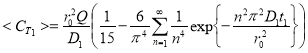
При справедливости сделанных выше некоторых приближениях можно считать, что поток газа из сферы при температуре Т2описывается уравнением:
J(t)=J1+J2=
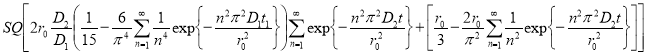 , (6)
, (6)
где D1 — коэффициент диффузии газа при температуре Т1, а D2- при температуре Т2.
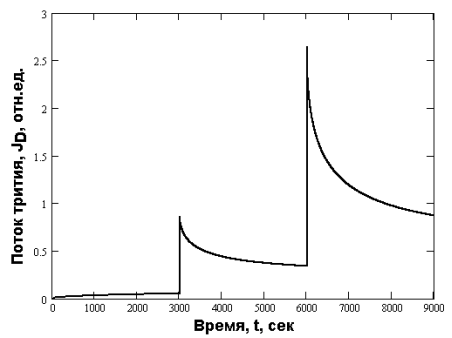
Рис. 2. Выделение трития, непрерывно генерируемого в сфере, при ступенчатом нагреве образца (Предполагается, что на предыдущих температурных ступенях гранула была полностью обезгажена; D1= 10–9 см2/сек, D2= 10–8 см2/сек, D3= 10–7 см2/сек, r0=0,1 см)
При больших временах t1:
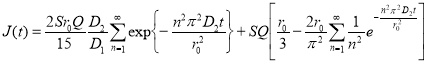 (7)
(7)
или
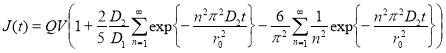 (8)
(8)
Если время t=t2 при температуре Т2достаточно велико, то устанавливается стационарное течение газа и
J=QV. (9)
Таким образом, при переходе от температуры Т1 к температуре Т2при справедливости сделанных выше некоторых приближений можно считать, что поток газа из сферы изменяется от закона при Т1:
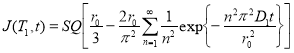 (10)
(10)
до закона при T2:
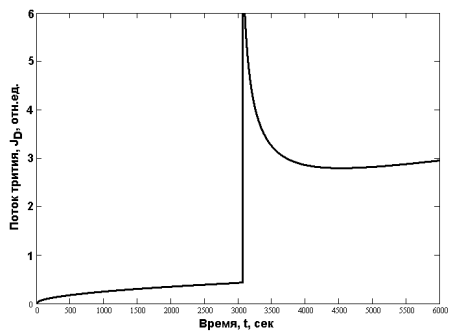
Рис. 3. Выделение трития, непрерывно генерируемого в сфере, при ступенчатом нагреве образца (Предполагается, что на предыдущих температурных ступенях гранула не была полностью обезгажена и содержала достаточное количество не успевшего выделиться трития; D1 = 10–9 см2/сек,D2= 10–8 см2/сек, D3= 10–7 см2/сек, r0=0,1 см)
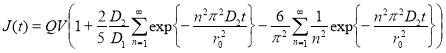 (11)
(11)
Аналогичные формулы описывают поведение потока стабильного газа при последующем ступенчатом нагреве до температур Т3, Т4, Т5 и т. п.
Отметим, что поскольку в поток при Т2входит не просто коэффициент диффузии, а отношение D2/D1, то из эксперимента по ступенчатому нагреву найти раздельно значения D1и D2невозможно.
В качестве примера, на Рисунке 3 представлено изменение во времени потока газа, непрерывно генерируемого в образце за счёт ядерной реакции, из сферы при резком увеличении температуры (и, следовательно, коэффициента диффузии. Видно, что сначала поток монотонно возрастает, стремясь к постоянному значению. В момент резкого возрастания температуры поток резко увеличивается, после чего монотонно спадает до значения, большего чем был на первой температурной ступени. При очередном резком повышении температуру вновь наблюдается повышение потока, причём большее, чем на предыдущей смене температур. Стационарный поток газа также выше, чем на предыдущей ступени).
Здесь мы считали, что на предыдущей температурной ступени образец полностью дегазировался. Если же в образце ещё достаточно трития, то его вклад в газовыделение на последующей температурной ступени существенен и, после некоторого падения, поток генерируемого газа начинает возрастать. Такое поведение потока не даёт возможность рассчитать коэффициент диффузии.
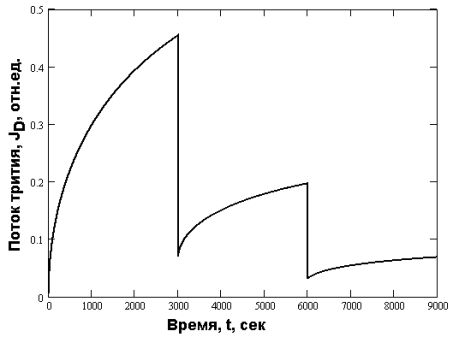
Рис. 4. Выделение трития, непрерывно генерируемого в сфере, при ступенчатом охлаждении образца ((D1= 10–7 см2/сек, D2= 10–8 см2/сек, D3= 10–9 см2/сек, r0=0,1 см)
Ступенчатое охлаждение.Перейдём теперь к рассмотрению поведения потока стабильного газа при ступенчатом охлаждении образца. Здесь уже T1
![]() (12)
(12)
Математический аппарат остаётся тем же, что был рассмотрен выше, но есть существенный нюанс.
Если Т1– достаточно высока и время t1 достаточно длительно, то газа в сфере практически не будет, т. е. ![]() . Это сильно упрощает ситуацию. Теперь уже поток стабильного газа при Т2изменяется по закону:
. Это сильно упрощает ситуацию. Теперь уже поток стабильного газа при Т2изменяется по закону:
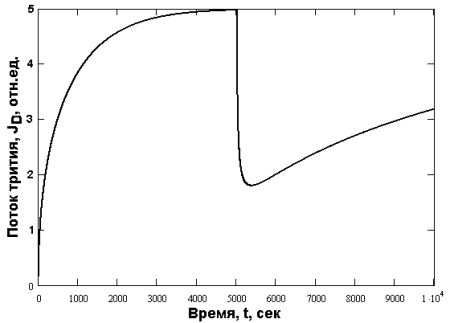
Рис. 5. Выделение трития, непрерывно генерируемого в сфере, с учётом присутствия трития, образовавшегося на предыдущей температурной ступени (ступенчатое охлаждение)
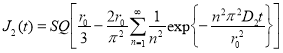 , (13)
, (13)
что позволяет найти единственный коэффициент диффузии D2.
На Рисунке 4 в качестве примера показано изменение потока трития из сферы при ступенчатом уменьшении температуры. Видно, что при резкой смене температуры поток резко падает, причём практически вертикально. Учёт частичной дегазации (т. е. наличия трития в образце при более высокой температурной ступени) приводит к более монотонного спаду потока в области смены температуры (Рисунок 5). Однако, время спада непродолжительно и не оказывает существенного влияния на форму кривой последующего подъёма потока генерируемого трития на новой температурной ступени.
Таким образом, анализ зависимости потока от времени позволяет при ступенчатом охлаждении найти коэффициент диффузии при низкой температуре, а при ступенчатом нагреве — сначала отношение D2/D1, затем уже (по кривым ступенчатого нагрева) — коэффициент диффузии при более высокой температуре.
Коэффициент диффузии трития по кристаллической решётке титаната лития
Приведённый в предыдущей главе математический аппарат диффузии был применён к обработке экспериментальных данных по выделению трития, непрерывно генерируемого из лития под действием нейтронов, в режиме термоциклирования литиевой керамики. Данные по выделению НТ и Т2 по данным ступенчатого охлаждения от высоких температур (при которых дегазация пэббла была достаточно большой) были пересчитаны в коэффициент диффузии тритона (Т+) по кристаллической решётке метатитаната лития, а затем уточнены по данным ступенчатого нагрева.
Обработка всего массива полученных в данных работе данных в рамках модели классической диффузии показала, что за год облучения литиевой керамики в реакторе, энергия активации диффузии существенно уменьшилась, что свидетельствует об уменьшении глубины потенциальных ям, по которым осуществляется диффузия тритона (Т+) по матрице твёрдого тела и выделение трития (в виде НТ и Т2) из образца. При этом величина предэкспоненциального (энтропийного) множителя тоже уменьшилась, что свидетельствует об уменьшении числа диффузионных путей, доступных для диффузии, вероятно вследствие создания радиационных дефектов, действующих, как ловушки диффундирующего трития.
Как обычно, мы полагали, что температурную зависимость коэффициента объёмной диффузии трития можно описать законом Аррениуса:
![]() , (14)
, (14)
где D(T) — коэффициент диффузии трития при температуре Т, ED — энергия активации диффузии, R=8,3144 Дж/мольоК — газовая постоянная, Т — температура в градусах Кельвина.
Оценки параметров аррениусовской зависимости коэффициента диффузии Т+ дали значения: D01=0,1 см2/сек и ЕD1=130 кДж/моль для начальной стадии выжигания лития и D02=0,006 см2/сек и ЕD2=69 кДж/моль для конечной стадии. Таким образом, пребывание тритиевой керамики в реакторе привело к уменьшению энергии активации диффузии трития почти в два раза и уменьшению пред экспоненциального (энтропийного) множителя диффузии более, чем на порядок.
Таблица 1
Значения коэффициентов диффузии вметатитанате лития при разных температурах иразных временах реакторного облучения.
|
Начальная стадия облучения |
Конечная стадия облучения |
||
|
Температура, оС |
Коэф. диффузии |
Температура, оС |
Коэф. диффузии |
|
300 500 700 |
1,3510–13 1,5910–10 1,0210–8 |
300 500 700 |
3,010–9 1,2810–7 1,1710–6 |
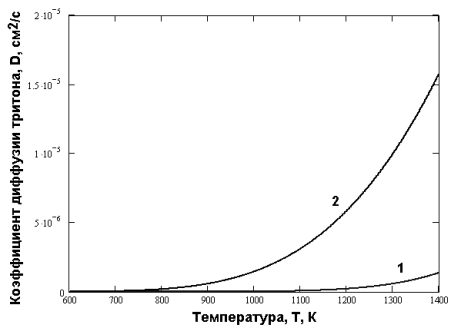
Рис. 6. Температурная зависимость коэффициента диффузии трития по объёму литиевой керамики для различных стадий выгорания 6Li: 1 — начальное реакторное облучение, 2 — конечное облучение
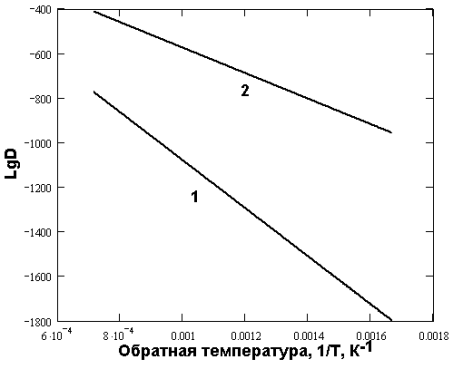
Рис. 7. Данные Рисунка 7, перестроенные в аррениусовских координатах
Теперь можно полуколичественно оценить характер изменения коэффициента диффузии трития при постоянной температуре в ходе выжигания. При температуре 500оС такую зависимость в первом приближении удалось описать формулой:
![]() , (15)
, (15)
где tr — время облучения литиевой керамики.
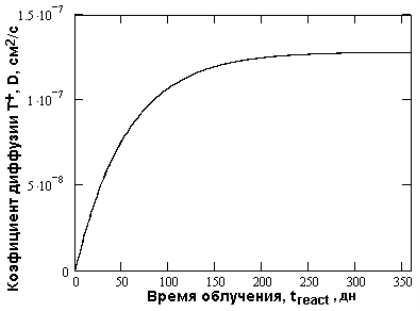
Рис. 8. Примерная зависимость, описывающая изменение коэффициента диффузии трития в метатитанате лития во время реакторного эксперимента
График этой функции D(tr) представлен на Рисунке 8. Из полученной зависимости следует, что коэффициент диффузии трития активно увеличивается только первые 10 месяцев реакторного облучения метатитаната лития, затем эффективный коэффициент диффузии стабилизируется на значении примерно 1,310–7 см2/сек и в дальнейшем не меняется или меняется очень слабо. По-видимому, достижение предельного значения коэффициента диффузии связано с противоположным действием двух факторов — 1) выжигания лития, приводящего к исчезновению ионов лития из узлов кристаллической решётки и связанного с этим облегчения диффузионного процесса и 2) возникновения под действием быстрых нейтронов и внешнего гамма-излучения радиационных дефектов, захватывающих диффундирующий тритий в ловушки и, следовательно, к затруднению диффузионных процессов. В работе [10] методом ступенчатого нагрева было показано, что энергия активации диффузии трития в LiAlO2 равна 141,5 кДж/моль, D0=0,13 см2/с, а время удержания трития в Li2Oc ростом температуры падает с энергией активации 56 кДж/моль [9]. Отметим, что полученные в этой работе значения D0 практически совпадают с рассчитанными нами из данных по ступенчатому охлаждению титаната лития.
Показано, что по мере облучения, создаваемые при выгорании лития дефекты действуют как дополнительные диффузионные пути, облегчающие диффузию трития. Выгорание трития компенсируется облегченной диффузией, в результате чего поток трития из керамики из титаната лития не меняется в течение достаточно длительного времени.
Литература:
- Chikhray, Y (Chikhray, Y.); Shestakov, V (Shestakov, V.); Kulsartov, T (Kulsartov, T.); Tazhibayeva, I (Tazhibayeva, I.); Kawamura, H (Kawamura, H.); Kuykabaeva, A (Kuykabaeva, A.) Measurement system for in-pile tritium monitoring from Li2TiO3 ceramics at WWRK reactor JOURNAL OF NUCLEAR MATERIALS Volume: 367 Pages: 1028–1032 AUG 1 2007
- T. Kurasawa, H. Watanabe, E. Roth, D. Vollath In-pile tritium release behavior from lithium aluminate and lithium orthosilicate of the VOM-23 experiment//J. Nucl. Mater., 155 157 (1988) 544–548.
- H. Moriyama, A. Okada, Y. Asaoka and Y. Ito The interactions of tritium with irradiation defects in solid breeder materials//J. Nucl. Mater., 179–181 (1991) 839–842.
- M. C. Billone, H. Attaya, J. P. Kopasz Modeling of tritium behavior in Li2O//, Argonne National Laboratory Rep., ANL/FPP/TM-260, August, 1992.
- M. C. Billone, G. Federici, A. R. Raffray, S Tanaka//Progress in tritium retention and release modelling for ceramic breeders//Fus. Eng. Des., v. 28 (1995) 240–251.
- ТажибаеваИ., КенжинЕ., ЧакровП., АринкинФ., ГизатулинШ., БекмухамбетовЕ., ШестаковВ., ЧихрайЕ., КульсартовТ., КуйкабаеваА., Kawamura H., Tshuchiya K.ИспользованиереактораВВР-Кдлядлительныхрадиационныхиспытанийлитиевойкерамики Li2TiO3 длябланкетаТЯР. — ВАНТ.СЕР. Термоядерныйсинтез, 2007, вып. 2, с. 3–10.
- ТажибаеваИ., ШестаковВ., КенжинЕ., ЧихрайЕ., КульсартовТ., КуйкабаеваА., БекманИ., ЧакровП., ГизатулинШ., Kawamura H., Tsuchiya K. Наработкатритиявлитиевойкерамике Li2TiO3 длябланкетатермоядерногореактора. — ВАНТ, Сер. Термоядерный синтез, 2008, вып.2, с. 3–12.
- Tazhibayeva, I., Chikhray Y., Shestakov V., Kulsartov T., Kykabaeva A., Kawamura H. Measurement System for In-pile Tritium Monitoring from li2tio3 Ceramics at wwrk. — J. Nucl. Mater., 2007, part 2., vol. 367–370, p. 1028–1032.
- Тажибаева И. Л., Кульсартов Т. В.? Кенжин Е. А., Максимкин О. П., Доронина Т. А., Осипов И. С., Сильнягина Н. С., Турубарова Л. Г., Цай К. В., Желтов Д. А., Каширский В. В., Чихрай Е. В., Шестаков В. П., Куйкабаева А. А., KawamuraH., TsuchiyaK. Структура, состав и свойства облученной в реакторе ВВР-К литиевой керамики Li2TiO3 +5 % мол. TiO2 для твердотельного керамического бланкета термоядерного реактора. — ВАНТ. Сер Термоядерный синтез, 2008, вып. 1, с. 3–12.
- A. Badawi, A. R. Raffray, M. A. Abdou//Analysis of tritium release from LiA1О2 in the TEQUILA experiment, using the MISTRAL code//Fus. Eng. Des.v. 17 (1991) 73–78
- A. R. Raffray, S. Cho, M. A. Abdou//Modeling of tritium transport in ceramic breeder single crystal//J. Nucl. Mater. v. 210 (1994) 143–160







