В статье рассматривается методика решения задачи оптимального раскроя материалов на заготовки средствами MSExcel.
Ключевые слова: математическая модель, критерий оптимальности, рациональный способ раскроя
Большинство материалов, используемых в промышленности, поступает на производство в виде стандартных форм. Непосредственное использование таких материалов, как правило, невозможно. Предварительно их разделяют на заготовки необходимых размеров. Это можно сделать, используя различные способы раскроя материала.
Задача оптимального раскроя состоит в том, чтобы выбрать один или несколько способов раскроя материала и определить, какое количество материала следует раскраивать, применяя каждый из выбранных способов. В качестве критерия выбора оптимальных способов раскроя могут быть использованы минимум отходов, минимальный расход материалов, максимум комплектов, включающих заготовки различных видов.
Задачи такого типа возникают в строительстве, машиностроении, лесной, деревообрабатывающей и лёгкой промышленности. От успешности их решения зависят экономия материалов и снижение отходов.
Рассмотрим методику решения задачи раскроя листовых материалов средствами MSExcel.
Пример. На предприятии имеются древесностружечные плиты (ДСтП) нескольких форматов, приведенные в таблице 1. Спецификация заготовок приведена в таблице 2. Требуется составить оптимальный план раскроя плит ДСтП на заготовки по критерию минимума отходов, при условии выполнения заданной спецификации заготовок.
Таблица 1
Спецификация плит ДСтП
|
№п/п |
Формат плиты, ммхмм |
Количество плит, шт. |
|
1 |
2440x1220 |
6000 |
|
2 |
1525x1525 |
8000 |
Таблица 2
Спецификация заготовок
|
№п/п |
Формат плиты, ммхмм |
Количество заготовок на годовую программу, шт. |
|
1 |
1000x600 |
12000 |
|
2 |
800x600 |
12000 |
|
3 |
600x600 |
18000 |
|
4 |
300x450 |
12000 |
|
5 |
300x300 |
24000 |
На первом этапе решения задачи определяются рациональные способы раскроя материала. Разрабатываются карты раскроя, представляющие собой графическое расположение заготовок на стандартном формате раскраиваемого материала.
При разработке карт раскроя требуется соблюдать следующие условия:
− максимальный выход деталей;
− минимальное количество типоразмеров деталей при раскрое одного формата любого материала;
− минимальное повторение одних и тех же деталей в разных картах раскроя;
− обеспечение минимума отходов [2, c. 49].
В нашем примере использовано шесть карт раскроя, по три для каждого размера древесностружечных плит. В таблице 3 приведён выход заготовок и площадь отходов.
Таблица 3
Расчет количества заготовок
|
Размер заготовки |
Количество заготовок, получаемых по карте раскроя, шт. |
|||||
|
Плита 2440x1220 |
Плита 1525x1525 |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
1000x600 |
4 |
- |
- |
- |
2 |
- |
|
800x600 |
- |
4 |
- |
- |
- |
2 |
|
600x600 |
- |
- |
8 |
- |
- |
2 |
|
300x450 |
- |
5 |
- |
6 |
5 |
- |
|
300x300 |
- |
- |
- |
15 |
- |
- |
|
Площадь отходов, м2 |
0,577 |
0,382 |
0,097 |
0,166 |
0,586 |
0,646 |
На втором этапе решается задача линейного программирования для определения интенсивности использования рациональных способов раскроя.
Составим математическую модель оптимизации.
В качестве неизвестных примем Хj — количество плит раскраиваемых j-м способом.
Целевая функция (минимум отходов):
F=0,577Х1+0,382Х2+0,097Х3+0,166Х4+0,586Х5+0,646Х6min
Система ограничений:
- по выпуску заготовок:
4Х1+2Х5=12000
4Х2+2Х6=12000
8Х3+2Х6=18000
5Х2+6Х4+5X5=12000
15Х4=24000
- по запасам сырья:
Х1+Х2+Х3<=6000
Х4+Х5+Х6<=8000
- по неотрицательности переменных:
Х1,…, Х6>=0
Симплекс-метод, основанный на идеях Л. В. Канторовича, был описан и детально разработан рядом ученых из США в середине 20 века. Надстройка MS Excel «Поиск решения» (Solver) использует этот алгоритм. Именно с помощью симплекс-метода и MS Excel мы будем решать задачу оптимального раскроя [3].
Оформим в MSExcel таблицу с исходными данными и введём формулы (рис.1):
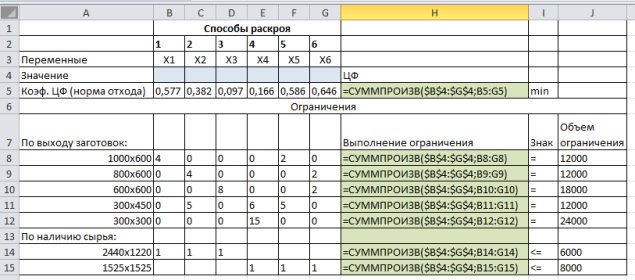
Рис. 1. Оформление таблицы с исходными данными в MSExcel
На вкладке «Данные» нажимаем кнопку «Поиск решения». Откроется диалоговое окно «Поиск решения», в котором указываем ячейку целевой функции, её направление, изменяемые ячейки и задаём ограничения задачи (рис. 2).
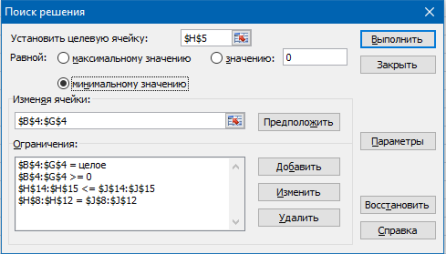
Рис. 2. Диалоговое окно «Поиск решения»
Щелчком по кнопке «Параметры» заходим в диалоговое окно «Параметры поиска решения» и устанавливаем флажок «Линейная модель». Нажимаем ОК. Выполняем поиск решения.
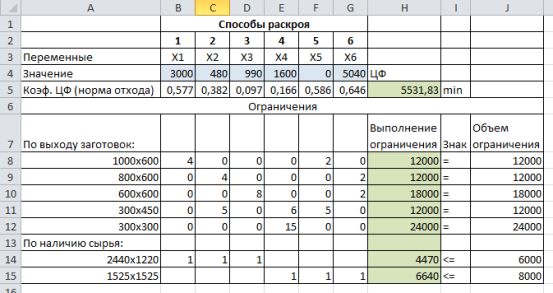
Рис. 3. Результат решения
На рисунке 3 показан оптимальный план раскроя. Следует раскроить древесностружечные плиты размера 2440х1220 первым способом 3000 шт., вторым способом 480 шт. и третьим способом 990 шт. Всего плит данного размера потребуется 4470 шт.
Древесностружечные плиты размера 1525х1525 следует раскроить четвертым способом 1600 шт. и шестым способом 5040 шт. Пятую карту раскроя использовать нерационально. Всего плит этого размера потребуется 6640 шт.
Полученный в оптимальном решении вариант использования карт раскроя плит обеспечит выполнение плана по выходу заготовок всех размеров. Отходы будут минимальными и составят 5531,83 м2.
Литература:
- Пижурин А. А. Основы моделирования и оптимизации процессов деревообработки / А. А. Пижурин. — М.: Лесная промышленность, 2004.
- Яцун И. В., Чернышев О. Н. Моделирование и оптимизация процессов деревообработки. Часть 1. — Екатеринбург: Редакционно-издательский отдел УГЛТУ, 2011.
- Линейный раскрой в Excel [Электронный ресурс] — Режим доступа: http://al-vo.ru/spravochnik-excel/linejnyj-raskroj-v-excel.html







