Работа выполнена при поддержке гранта РФФИ №16-08-00243 а
В данной статье описаны исследования ветровых турбин типа Савониуса. Представлены основные направления изучения (повышения эффективности) работы ротора Савониуса. Были выделены основные преимущества каждого из этих направлений. Рассмотрены двумерное и трехмерное компьютерное моделирование, влияние формы лопасти на энергетическую эффективность ротора. При этом был сделан вывод, что инновационная модификация классического дизайна ротора Савониуса показывает более высокую эффективность, за счет более высокого коэффициента мощности.
Ключевые слова: ротор Савониуса, ветрогенератор, ветровой поток, аэродинамика, математическая модель.
Среди вертикальных ветрогенераторов можно выделить следующие группы роторов: ортогональный, Савониуса, Дарье, Геликоидный, многолопастной с направляющим аппаратом. Основным достоинством вертикальных ветрогенераторов является отсутствие необходимости ориентировать их на ветер. Одним из недостатков, ограничивающих диапазон их применения и их единичную мощность, является их более низкая эффективность работы, по сравнению с горизонтально-осевыми ветрогенераторами, при одинаковых ометаемых площадях и более высокая материалоемкость, при одинаковой мощности.
На сегодняшний день конкурентоспособными по сравнению с горизонтально-осевыми (ГО) ветроэнергетической установки (ВЭУ) являются вертикально-осевой (ВО) ВЭУ с ротором типа Дарье. Однако они обладают существенным недостатком – малым стартовым крутящим моментом, что приводит к проблеме самозапуска. Даже если ротор Дарье под действием набегающего потока ветра начнет движение, то существуют так называемые «мертвые точки», при попадании в которые ротор не сможет самостоятельно выйти из этого положения. Хотя практика эксплуатации ВЭУ показывает, что за счет наличия порывов ветра ротор Дарье в состоянии запуститься самостоятельно. Кроме того, на практике осуществляют подход, когда после штиля ветер набирает скорость, соответствующую минимальному порогу выработки электроэнергии, генератор ВЭУ переводится в режим двигателя (до 15 секунд), ротор раскручивается и начинает работать, не дожидаясь порога самозапуска [10, 11].
Изобретение ротора S-образной формы принадлежит скандинавскому изобретателю Савониусу. Данный тип ротора вобрал в себя такие положительные качества как дешевизна конструкции, простота исполнения, возможность работы при различных направлениях ветрового потока, низкий уровень шума, а наиболее важным качеством является большой пусковой аэродинамический момент [7].
Но ротор Савониуса имеет важный отрицательный момент — это низкая эффективность его работы. Не смотря на то, что данный тип ротора имеет большой пусковой момент, во время постоянной работы он максимально может выдавать мощность не более 5 кВт. Отсюда видно, что такие установки могли бы быть выгодны в сельской местности. Можно так же отметить, что данный тип конструкции часто используют в сочетании с ротором Дарье, который в свою очередь имеет высокую эффективность работы, но низкий пусковой аэродинамический момент [8].
В качестве лопастей в роторе Савониуса используются два или несколько полуцилиндров. Для ротора Савониуса характерны высокие пусковые крутящие моменты, работа при относительно низких скоростях и относительно высокая технологичность его производства. Недостатками ротора Савониуса являются: более низкая эффективность работы лопастной системы, по сравнению с горизонтально-осевыми ВЭУ; относительно высокая материалоемкость. В настоящее время ветрогенераторы с ротором Савониуса выпускаются в диапазоне мощностей до 5 кВт. Ротор Савониуса, так же, часто комбинируют с ротором Дарье, для обеспечения более высоких пусковых моментов ротора Дарье [7, 9].
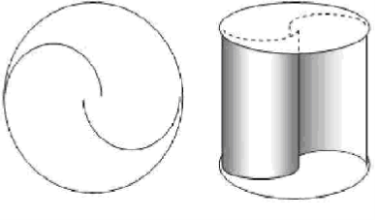
Рис.1. Классический вид ротора Савониуса
Исследование ветровых турбин, таких как турбина Савониуса и его модификаций, происходит в соответствии с общей стратегией развития энергетики Европейского Союза [11]. Эта стратегия имеет тенденцию по увеличению общего количества использования возобновляемых источников энергии. Но развитие в этой области значительно тормозится из-за высоких цен на установки, работающих на возобновляемых источниках энергии, в том числе и на ветроэнергетические установки (ВЭУ).
Рассмотрим современные тенденции развития ВЭУ с ротором Савониуса:
В работе [1] приведено исследование мало-изогнутого Савониуса, для подтверждения численных результатов, полученных с помощью вычислительной динамики жидкости и газа(метод CFD). Изготовленный ротор Савониуса высотой 300 мм и диаметром лопасти 100 мм был помещен в аэродинамическую трубу с размерами 400 мм х 400 мм. Данный прототип был использован для оценки профилей скорости. Измерения скорости воздушного потока производилась термоанемометром, а скорость воздушного потока на испытательном участке варьировалась от 0 до 17 м/с.

Рис.2. Мало-изогнутый ротор Савониуса
В ходе анализа выявлено, что аэродинамическое поведение ротора Савониуса изучено в значительной степени, но несоответствие условий проведения исследований затрудняет сравнение полученных результатов. Для того, чтобы проверить надежность модели, была реализована экспериментальная проверка. Значения скорости были взяты из области вокруг ротора в испытательной секции. Использование анемометра, несколько значений скорости были собраны в разных плоскостях. Экспериментальная проверка показала сравнимые результаты экспериментальных и численных значений скорости. Числовую модель можно считать достоверной. Действительно, кажется, что эта модель способна прогнозировать аэродинамические характеристики потока.
В работе [2] были рассмотрены вопросы повышения эффективности ротора путем определения его оптимальных геометрических параметров. Так предлагается использовать ротор Савониуса с двумя лопастями и двумя торцевыми пластинами. Высота ротора должна быть вдвое больше его диаметра. Отношение первичных нахлестов должно быть в пределах от 0,15 до 0,3 от диаметра лопасти, тогда как коэффициент вторичных нахлестов должен быть равен 0.

Рис.3. Пример распределения полей скорости ветрового потока в роторе Савониуса
Это исследование соответствует численному моделированию потока. Результаты моделирования предлагают оптимальные значения для геометрических параметров. Это моделирование приводит не только к точному характеру потока, но и определяют аэродинамическое поведение ротора. Результаты сравниваются с экспериментальными данными. В частности, прогнозирование аэродинамических моментов для нескольких геометрических конфигураций. Изучено влияние центрального вала, такое как наличие и геометрия внешнего шасси. Исследовано влияние числа Рейнольдса. Эти исследования позволяют определить оптимальную геометрическую конфигурацию.
Это исследование было реализовано в двух направлениях. Во-первых, библиографическое исследование выявило основные геометрические параметры. Тогда численное моделирование по оценкам этого влияния и предложило оптимальные значения для этих геометрических параметров. В результате неоспоримы более высокие значения коэффициента мощности т.е. аэродинамической эффективности ротора. В дальнейшем решено разработать в 3-D программах другие формы лопасти для повышения эффективности такого ротора.
В работе [3] проведено численное исследование нетрадиционного ротора Савониуса с дугой 75°. В данной работе с помощью компьютерного моделирования было проведено изучение аэродинамической структуры нетрадиционного ротора Савониуса с углом дуги ковша 75°. Численная модель основана на решении уравнений Навье-Стокса в сочетании со стандартной моделью турбулентности. Эти уравнения были решены с помощью метода конечных объемов дискретизации. Программное обеспечение «SolidworksFlowSimulation» используется для описания характеристик потока в разных поперечных и продольных плоскостях. Хорошее сравнение между численными и экспериментальными результатами подтверждает правильность численного метода.
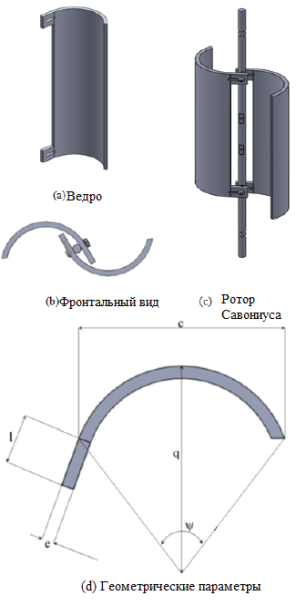
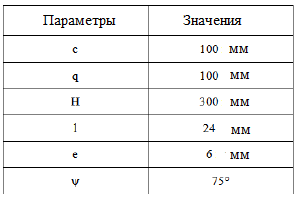
Рис.4. Модифицированный ветровой ротор Савониуса
Исследование показало, что с помощью компьютерного моделирования было проведено изучение аэродинамической структуры вокруг нетрадиционного ротора Савониуса с углом дуги ковша 75°. В этой работе было обнаружено, что конструкция ковша оказывает непосредственное влияние на локальные характеристики. В частности, было отмечено, что декомпрессионная зона расположена в вогнутой поверхности ковша и ниже по течению от ротора. Зона ускорения, где отмечены максимальные значения скорости, сформирована в выпуклой поверхности ковша ротора. В будущем, мы предполагаем использовать лазерную систему велосимметрии изображения частиц (PIV) для анализа локальных характеристик воздушного потока вокруг нетрадиционным ветра роторов Савониуса.
Следующая работа [4] рассматривает такие вопросы как, CFD прогнозирование модифицированного ротора Савониуса с новой формой лопасти. В этом исследовании ветровая турбина Савониуса представляет собой тип вертикально-осевой ветровой турбины (VAWTs), состоящей из двух или трех лезвий дуги, которая может вырабатывать энергию даже при плохих условиях ветра. Модифицированная ветровая турбина Савониуса с новыми формами лезвий введена с целью повышения коэффициента мощности турбины. Эффект лезвий, форма лопасти, двухлопастного ветродвигателя Савониуса исследована с помощью вычислительной гидродинамики (CFD). Моделирование основано на осредненных по Рейнольдсу уравнениях Навье-Стокса. Этот численный метод подтверждается существующими экспериментальными данными, а затем используется для количественной оценки производительности при различных вариантах исполнения. Результаты количественного определения взаимосвязи между исполнениями лезвий турбины приводит к высокому коэффициенту мощности, 0.2573. Этот коэффициент мощности 10,98% выше, чем у обычного ротора Савониуса.

Рис.5. Сетка для генерации (а) домена станции и (б) пограничных слоев.
Анализ представлен методикой проектирования для определения геометрии ветровых турбин Савониуса. Для количественного определения аэродинамической производительности ротора, порожденной вариантами дизайна, было выполнено двумерное моделирование CFD. Было изучено влияние полноты лопасти на производительность турбины. На основе результатов работы были сделаны следующие выводы:
1) Ротор с лезвиями полнотой n = 1 имеет самый высокий коэффициент мощности, 0,2573, который на 10,98% выше, чем у обычного Савониуса турбины.
2) За период вращения, лезвие с меньшей наполненностью генерирует как более положительный крутящий момент значения, так и более низкие отрицательные значения крутящего момента.
3) Турбины с n ≤ 1, имеют более широкие лопасти, чем те, n> 1.
В работе [5] рассматривается, статическое и динамическое исследование обычного ротора Савониуса с помощью численного моделирования. Исследование осуществляется с использованием численного моделирования в программном модуле CFD. Аэродинамические величины, такие как давление, скорость и аэродинамические силы, рассчитываются, для получения рабочих кривых ротора. В любом случае, численный метод зависит, например, от типа и количества ячеек в сетке, законов газодинамики. В работе представлен метод «вращающийся ротор». Показано, что статические и динамические расчеты находятся в хорошем соответствии с литературой в этой области.

Рис. 6. Поле потока вокруг ротора при θ=45°
В ходе работы сделан вывод, что численное двумерное моделирование было проведено, чтобы предсказать поведение аэродинамики ротора Савониуса. Численный метод был объяснен, например, моделью турбулентности. Две модели были протестированы: круговая и классическая прямоугольная. Результаты были сопоставлены с различными экспериментами, особенно с работами Блэквелла и др. [10], данные согласуются с экспериментальными данными. В будущем планируется провести расчет трехмерного объекта, результаты которого будут сопоставлены с экспериментами.
В следующей работе [6] рассмотрены вопросы по теме: Верификация комплекса математических моделей аэродинамики и динамики движения ротора Савониуса.
В данном исследовании представлены основные этапы верификации комплекса математических моделей аэродинамики и динамики движения ротора Савониуса, основанных на методе дискретных вихрей. Результаты расчётов приводятся в сравнении с данными численных и опытных экспериментов.
По результатам верификации предлагаемого комплекса математических моделей можно сделать вывод, что программный продукт может быть использован для решения широкого спектра задач, стоящих перед ветроэнергетикой:
1) создание каталога типоразмеров ВЭУ с заданной геометрией роторов, позволяющего определить зависимость выходных (мощностных) характеристик от скорости ветра, диаметра ротора, удлинения лопастей;
2) определение, оптимальной с точки зрения эффективности использованияэнергии ветра, геометрии лопастей роторов (имеющих форму дуги окружности, части лемнискаты, дуги эллипса и т. п.) для уже существующих конструкций ВЭУ с вертикальной осью вращения;
3) разработка новых конструктивных схем ВЭУ;
4) моделирование динамики выхода ВЭУ на рабочий режим;
5) моделирование поведения ВЭУ при непредвиденных обстоятельствах (например, при внезапном увеличении скорости ветра выше запланированногозначения);
6) расчет нагрузки на элементы ВЭУ (например, на опоры валов).
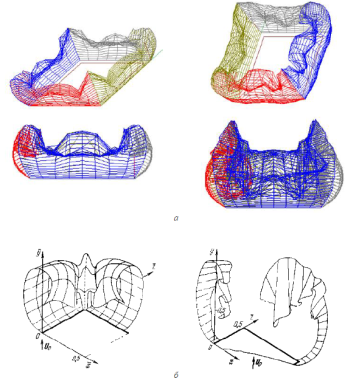
Рис.7. Рассчитанный вихревой след за неподвижной плоской пластиной в различные моменты безразмерного времени τ:τ = 1 (слева), τ = 2,5 (справа); а — авторы, б — работа
Рассмотрев наиболее перспективные направления изучения ротора Савониуса можно сделать вывод, что трехмерный анализ переходных аэродинамических явлений, происходящих в инновационной модификации классической ветротурбины Савониуса, включает в себя как переходные расчеты CFD, так и последовательные эксперименты в аэродинамической трубе. Инновационная модификация классического дизайна Савониуса показывает более высокую эффективность.
Литература:
1. Driss Zied, Mlayah Olfa, Driss Slah, Maaloul Makram, Abid Mohamed Salah. Study of a Small Incurved Savonius Wind Rotor: Experimental Validation //International Journal of Mechanics and Applications. – 2015. – Т. 5. – №. 2. – С. 31–36.
2. Menet J. L., Bourabaa N. Increase in the Savonius rotors efficiency via a parametric investigation //Proc. of European wind energy. – 2004.
3. Driss Zied, Mlayah Olfa, Driss Slah, Maaloul Makram, Abid Mohamed Salah. Numerical Study of an Unconventional Savonius Wind Rotor with a 75° Bucket Arc Angle //American Journal of Mechanical Engineering. – 2015. – Т. 3. – № 3A. – С. 15–21.
4. TianW., Song B., Van Zwieten J. H., Pyakurel P. Computational fluid dynamics prediction of a modified Savonius wind turbine with novel blade shapes //Energies. – 2015. – Т. 8. – № 8. – С. 7915–7929.
5. Menet J. L., De Rezende T. Static and dynamic study of a conventional Savonius rotor using a numerical simulation //21è CongrèsFrançais de Mécanique (CFM). – 2013.
6. Сизов Д. А., Онушкин Ю. П., Краснова О. А., Джанибеков О. Т. Верификация комплекса математических моделей аэродинамики и динамики движения ротора Савониуса // Вестник Самарского государственного аэрокосмического университета, 2013. –№ 1 (39). – С. 148–155.
7. Altan B. D., Atılgan M. A study on increasing the performance of Savonius wind rotors // Journal of mechanical science and technology. – 2012. – Т. 26. – № 5. – С. 1493-1499.
8. Баев В. И., Прокофьев Н. В. Повышение эффективности ветроэнергетической установки тип Савониуса //НАУЧНЫЕ ОСНОВЫ СТРАТЕГИИ РАЗВИТИЯ АПК И СЕЛЬСКИХ ТЕРРИТОРИЙ В УСЛОВИЯХ ВТО материалы международной научно-практической конференции, посвящённой 70-летию образования ВолГАУ, 2014. – С. 449–453.
9. Казакова М. В., Мингазетдинов И. Х. Комбинированный ветродвигатель //Всероссийская молодежная конференция «Современные аспекты энергоэффективности и энергосбережения»: сборник материалов.– М-во образ. и науки России, Казанский национальный исследовательский технический университет им. А.Н. Туполева. – Казань: Изд-во КНИТУ, 2013.– С.63–64.
10. Редчиц Д. А., Приходько А. А. Аэродинамика роторов Дарье и Савониуса //Авиационно-космическая техника и технология. – 2007. – №. 5. – С. 26–31.
11. Tesch K., Kludzinska K., Doerffer P. Investigation of the Aerodynamics of an Innovative Vertical-Axis Wind Turbine //Flow, Turbulence and Combustion. – 2015. – Т. 95. – № 4. – С. 739–754.







