Математическая модель взаимодействия творческих субкультур
Колпак Евгений Петрович, доктор физико-математических наук, профессор;
Гаврилова Анна Васильевна, студент
Санкт-Петербургский государственный университет
На основе анализа творческой среды, возникшей вокруг художника К. П. Брюллова, предлагается математическая модель трех взаимодействующих субкультур. Модель представлена задачей Коши для системы трех дифференциальных уравнений.
Ключевые слова: субкультура, живопись, математическое моделирование
Введение. Математическому моделированию социальных систем сейчас уделяется значительное внимание. В основном это связано с задачами формирования эффективно работающих коллективов и объединений людей, возникающими в структурах рыночной экономики [2, 9, 10, 15, 21, 22, 29, 41–43, 54]. Во втором направлении развиваются модели самоорганизации социальных групп, возникающих в обществе [1, 16, 17, 19, 23, 24, 28, 32–34, 39, 47, 49, 53]. Большинство моделей этого направления основывается на работах специалистов, объясняющих причины возникновения социальных групп и их эволюцию [4, 16, 27, 34, 44–46, 49, 52, 53]. Статистические данные или количественные характеристики при построении моделей используются редко. Это обусловлено, прежде всего, тем, что исследуемые объекты и системы являются трудно формализуемыми. В работе на основе анализа творческой среды, возникшей вокруг художника К. П. Брюллова, предлагается математическая модель взаимодействующих субкультур. За основу модели взята модель протокооперации, разработанная в [4, 18].
Творческой субкультурой называют определенную группу людей, где досуг дополняет профессиональную деятельность, соединяет труд и отдых в одно целое. Труд субкультур художников, литераторов, композиторов, ученых состоит в творческом искании [16]. В общении людей творческого труда формируется образ действительности, который в их интерпретации отображается в литературных, музыкальных, художественных и других произведениях [31, 40]. Создаваемые ими произведения, являются одним из источников знаний, движущей силой культурного развития общества и его исторической памятью [20]. Одной из субкультур, возникшей в далеком прошлом, является субкультура художников.
Процесс становления художников, произведения которых со временем получают широкое признание, очень сложный. У каждого из них свой творческий путь, но есть и то, что характерно для большинства из них. Общим является их творческое взаимодействие не только внутри самой субкультуры художников и с представителями других субкультур, но и со всеми слоями общества. Число и значимость создаваемых ими произведений зависят не только от личных качеств художника, но и от широты его контактов внутри общества [7, 11, 26, 31, 35–38]. Не менее важным является понимание решаемых задач и методов их решения различными субкультурами, существовавшими в прошлом [20].
Художник Карл Павлович Брюллов. К числу русских художников XIX века, оставивших значимый след не только в российской культуре [6, 25], но и в мировой, относится К. П. Брюллов (1779–1852). Он родился в семье, в которой из поколения в поколение передавались профессиональные традиции художников [3, 25, 26, 31]. Отец Карла Брюллова был членом академии художеств, известным резчиком по дереву. Семья имела многочисленные контакты с художниками, музыкантами, писателями, актерами. То есть Карл Брюллов с раннего детства рос в творческой обстановке и учился основам живописи. В девятилетнем возрасте Брюллов поступает учиться в Академию художеств. И здесь начинает формироваться его окружение друзей: художников, артистов, писателей, ставших известными в будущем. Учеба в академии длилась 12 лет. В 1821 году Карл Брюллов начинает свой самостоятельный путь художника [3, 25, 35].
Первый год самостоятельной творческой работы Брюллова сопровождался расширением круга его знакомств с художниками, актерами императорского театра, общественными деятелями. На его способности обратило внимание Общество поощрения художников, которое предложило ему пенсион для поездки в Италию на три года для изучения работ классиков западноевропейского искусства. Поездка в Рим длилась восемь месяцев и сопровождалась изучением и анализом работ западноевропейских художников в музеях Риги, Мюнхена, Венеции и других городов Европы [3].
В Риме центрами притяжения творческой интеллигенции были дома графа Д. П. Бутурлина и российского посланника князя Г. И. Гагарина, салон З. А. Волконской [3, 7]. Очень быстро и студия Брюллова, созданная им в Италии, стала местом притяжения российских и западноевропейских художников, писателей, общественных деятелей, оказавших влияние на его творчество [3, 5, 11, 13, 14, 25, 30]. Это художники И. Фумагалли и А. К. Варнек, архитекторы Х. Ф. Мейер, Л. Кленце и К. Тон, писатели и ученые К. Н. Батюшков, Стендаль (Мари-Анри Бейль), Ф. Д. Гверацци, П. Я. Чаадаев, скульптор Т. Вагнер, музыканты М. Ю. Виельгорский и Ф. Персиани, меценаты В. П. Давыдов и А. Н. Демидов. В общении с участниками творческих субкультур у Брюллова постоянно появляются новые образы, навеянные евангельскими сюжетами, античными мифами, событиями древней истории [3].
За тринадцать лет творчества в Италии Брюллов наряду с портретной живописью [8] осваивает качественно новый жанр — историческую живопись. Его произведение «Последний день Помпеи», над которым он работал около пяти лет, стало наиболее значим произведением, созданным в Италии [6]. В 1833–1834 с шедевром знакомится общественность Европы и России. Тринадцать лет напряженной творческой деятельности поставили Карла Брюллова в ряд величайших деятелей русского и западноевропейского искусства.
Следующий этап творчества начинается, организованным в 1834 году меценатом В. П. Давыдовым, путешествием сначала в Грецию, а затем в Турцию [3]. Поддержку в экспедиции Брюллову оказывают архитектор Н. Е. Ефимов и археолог И. Крамер. В Греции и Турции в круге его друзей появляются не только новые общественные и политические деятели, но и российские флотоводцы. Работа над новыми сюжетами не прекращается.
В 1835 году Брюллов возвращается в Россию. В круг его друзей вливаются ведущие российские писатели и поэты (А. А. Пушкин, В. А. Жуковский, И. А. Крылов, В. Г. Белинский, Н. В. Гоголь, М. Ю. Лермонтов, Е. А. Баратынский), художники (В. А. Тропинин, Е. И. Маковский), композиторы (А. С. Доргомыжский, М. И. Глинка), актеры (М. С. Щепкин, Е. С. Семенова, В. Н. Асенкова, П. Виардо, С. И. Самойлова). Начинается создание замечательной галереи портретов русских писателей, художников, артистов, общественных деятелей [3, 36, 40]. Расширяется круг его поклонников, оказывавших моральную и материальную поддержку (меценаты Ю. П. Самойлова и великая княгиня Елена Павловна). В этот период его творчества изменяются и технические приемы написания картин. Накопленные образы в Италии, Греции и Турции позволили художнику не только продолжать работать над портретами и историческими сюжетами, но приступить к монументальной и декорационной живописи: работать над оформлением плафонов церквей и соборов, оформлением декораций.
В 1849 году Карл Брюллов уезжает сначала в Португалию, а затем в Италию. Посещая страны Европы, мастер продолжает знакомиться с работами западноевропейских художников и реализовывать свои замыслы [3]. Его творческий путь заканчивается в Италии в 1852 году.
Все периоды творчества Карла Брюллова сопровождались контактами с представителями различных творческих субкультур, в общении с которыми возникали новые сюжеты, воплощенные впоследствии в художественных произведениях, как самого художника, так и его оппонентов. Материальную поддержку оказывали друзья, меценаты, общественные организации. В общей сложности у Брюллова состоялись только описанные в различных литературных источниках контакты не менее чем с 1500 представителями различных социальных и творческих групп, и более 400 контактов, отраженных в его произведениях. Значительная часть задуманных сюжетов, возникших в результате общения с представителями творческих субкультур, была реализована в произведениях художника.
Математическая модель протокооперации двух популяций. Протокооперация популяций является симбиотическим отношением полезным для каждой из них, но не обязательным — каждая популяция может существовать независимо от партнеров. Модель протокооперации двух популяций, предложенная в [4], представлена системой дифференциальных уравнений
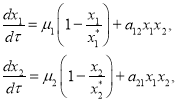 ,(1)
,(1)
где ![]() и
и ![]() — численности популяций,
— численности популяций, ![]() и
и ![]() — удельные скорости роста популяций при их малой численности,
— удельные скорости роста популяций при их малой численности, ![]() и
и ![]() — константы, характеризующие скорости влияния популяций друг на друга,
— константы, характеризующие скорости влияния популяций друг на друга, ![]() и
и ![]() — максимальные численности популяций в отсутствии влияния друг на друга
— максимальные численности популяций в отсутствии влияния друг на друга
Замена ![]() ,
, ![]() ,
, ![]() переводит систему уравнений (1) в
переводит систему уравнений (1) в
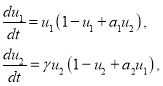 (2)
(2)
где ![]() ,
, ![]() ,
, ![]() .
.
Стационарные точки этой системы уравнений ![]() ,
, ![]() и
и ![]() будут неустойчивыми. Стационарная точка
будут неустойчивыми. Стационарная точка
![]() ,
, ![]()
будет иметь физический смысл, если выполняется неравенство ![]() . В этом случае эта стационарная точка будет устойчивой [12, 48, 50, 51], поскольку характеристический полином матрицы Якоби правой части уравнений (2)
. В этом случае эта стационарная точка будет устойчивой [12, 48, 50, 51], поскольку характеристический полином матрицы Якоби правой части уравнений (2)
![]()
будет иметь корни с отрицательной вещественной частью. Таким образом, в модели протокооперации (2) возможен неограниченный рост численности популяций при достаточно сильном благотворном влиянии их друг на друга (при ![]() ).
).
Реальная взаимная поддержка субкультур ограничена. В модели (2) это учитывается следующим образом [4, 18]
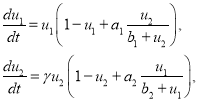
где ![]() и
и ![]() — константы.
— константы.
Нетривиальная стационарная точка этой системы уравнений является корнем системы уравнений
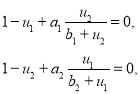
которая имеет единственное решение такое, что ![]() и
и ![]() . При этом вещественные части собственных значении матрицы Якоби
. При этом вещественные части собственных значении матрицы Якоби
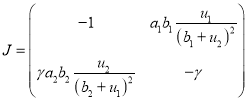
правой части уравнений будут иметь отрицательные вещественные части. Соответственно эта стационарная точка будет устойчивой.
Математическая модель взаимодействующих субкультур. В математических моделях популяционной динамики основными характеристиками являются численности популяций и трофический ресурс. В моделях социальной самоорганизации в роли трофического ресурса выступают образы и идеи, объединяющие отдельные личности в субкультуру с возникшим в ней групповым сознанием. Творчество писателей, художников, композиторов, актеров происходит в социальной среде их субкультур с постоянным обменом идеями между ними. Но воплощение замыслов в произведениях, как правило, осуществляется самостоятельно, при этом один и тот же сюжет может быть представлен в произведениях различных по технике исполнения (музыкальное, литературное, драматическое и т. д.). Созданные в творческих субкультурах произведения, как правило, становятся востребованными в обществе, а из любителей соответствующего жанра формируется субкультура меценатов.
В качестве основной характеристики, описывающей динамику числа образов, можно взять количество созданных художником произведений. На рис. 1 отражено изменение числа произведений живописи, созданных К. Брюлловым на протяжении всей его жизни (по данным [3]). Символом «звездочка» отмечены статистические данные. Как следует из анализа этих данных, эта зависимость на начальном участке близка к экспоненциальной зависимости (на рис. 1 — сплошная линия). Замедление скорости роста числа созданных произведений в 1840-е годы объясняется переходом художника к новым жанрам — монументальной живописи.
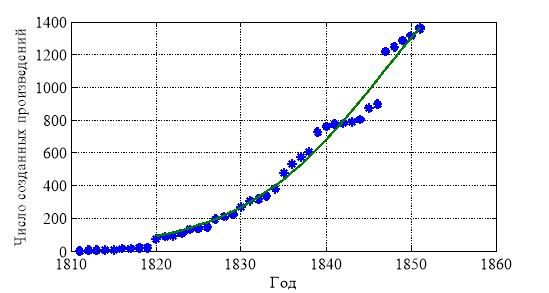
Рис. 1
Пусть ![]() – число образов, которое художник может реализовать за все время своего творчества, а
– число образов, которое художник может реализовать за все время своего творчества, а ![]() – число образов, которое он уже создал. Тогда скорость изменения числа образов должна быть пропорциональна числу образов, которые он уже реализовал в своих произведениях, и доле тех образов, которые он еще может реализовать из оставшихся у него. Тогда скорость изменения числа образов описывается уравнением
– число образов, которое он уже создал. Тогда скорость изменения числа образов должна быть пропорциональна числу образов, которые он уже реализовал в своих произведениях, и доле тех образов, которые он еще может реализовать из оставшихся у него. Тогда скорость изменения числа образов описывается уравнением
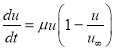 ,(3)
,(3)
где ![]() — константа. Для данных, отображенных на рис. 1
— константа. Для данных, отображенных на рис. 1 ![]() .
.
При экспоненциальном росте числа созданных произведений удельная скорость роста постоянна, для логистического уравнения (3) текущая удельная скорость роста убывает.
Однако, как следует из анализа статистических данных, текущая скорость увеличения числа созданных произведений у художника росла. Так, например, в таблице 1 отражено число произведений созданных Брюлловым за год на четырех этапах его творческой деятельности. Поэтому, несмотря на количественное совпадение теоретических и статистических данных (рис. 1), уравнение (3) не отражает внутреннюю систему взаимоотношений представителей творческих субкультур, влияющих на скорость и количество создаваемых произведений художником.
Таблица 1
|
Годы |
Страна |
Среднее число созданных произведений за год |
|
1810–1821 |
Россия |
16 |
|
1822–1834 |
Италии, Греция |
40 |
|
1835–1848 |
Россия |
80 |
|
1849–1852 |
Италия |
22 |
В математической модели взаимодействующих субкультур учтем три субкультуры, влияющие друг на друга: субкультуру, создающую конкретные художественные произведения, субкультуру, помогающую генерировать первой новые образы, и субкультуру меценатов, оказывающую «техническую» поддержку первой. В модели учтем, что все три субкультуры могут существовать независимо друг от друга и логика их внутреннего развития, направленная на создание материальных и информационных ресурсов, может быть описана логистическим уравнением. Для субкультуры меценатов это могут быть созданные или накопленные материальные ресурсы, а для творческой субкультуры это могут быть разработанные сюжеты в рамках своих произведений и переданные участникам первой субкультуры. Вторая субкультура увеличивает число образов первой субкультуры, а участие субкультуры меценатов направлено на увеличение скорости создания произведений первой субкультуры. Часть участников второй субкультуры может перейти в субкультуру меценатов.
Пусть ![]() — число образов, воплощенных в произведения представителями первой субкультуры,
— число образов, воплощенных в произведения представителями первой субкультуры, ![]() — число образов, возникающих во второй субкультуре и передаваемых первой,
— число образов, возникающих во второй субкультуре и передаваемых первой, ![]() — число действующих со стороны меценатов материальных факторов, увеличивающих скорость роста числа образов первой субкультуры. Тогда модель взаимодействия таких трех субкультур представлена системой трех обыкновенных дифференциальных уравнений:
— число действующих со стороны меценатов материальных факторов, увеличивающих скорость роста числа образов первой субкультуры. Тогда модель взаимодействия таких трех субкультур представлена системой трех обыкновенных дифференциальных уравнений:
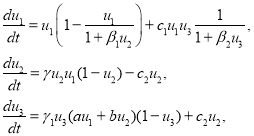 (4)
(4)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() — константы. При этом считается, что
— константы. При этом считается, что ![]() .
.
В этой модели предполагается, что при малых значениях ![]() и
и ![]() число произведений, создаваемое первой субкультурой, описывается логистическим уравнением (3). То есть вторая субкультура и субкультура меценатов не оказывают существенное влияние на первую субкультуру. Влияние второй субкультуры на первую учтено в первом уравнении множителем
число произведений, создаваемое первой субкультурой, описывается логистическим уравнением (3). То есть вторая субкультура и субкультура меценатов не оказывают существенное влияние на первую субкультуру. Влияние второй субкультуры на первую учтено в первом уравнении множителем ![]() — вторая субкультура передает часть своих образов первой. Слагаемое
— вторая субкультура передает часть своих образов первой. Слагаемое ![]() в первом уравнении учитывает влияние субкультуры меценатов на скорость роста числа образов при непосредственном контакте с представителями первой субкультуры, но это влияние ограничено. Последнее учтено наличием множителя
в первом уравнении учитывает влияние субкультуры меценатов на скорость роста числа образов при непосредственном контакте с представителями первой субкультуры, но это влияние ограничено. Последнее учтено наличием множителя ![]() .
.
Вторая субкультура, поддерживающая первую, создает образы для первой субкультуры при непосредственном контакте с ней или через свои произведения (множитель ![]() в первом слагаемом второго уравнения в (4)), или передав их в субкультуру меценатов (слагаемое
в первом слагаемом второго уравнения в (4)), или передав их в субкультуру меценатов (слагаемое ![]() во втором уравнении). Количество образов, создаваемых ею, ограничено (множитель
во втором уравнении). Количество образов, создаваемых ею, ограничено (множитель ![]() в первом слагаемом второго уравнения).
в первом слагаемом второго уравнения).
Субкультура меценатов оказывает поддержку первой субкультуре при непосредственном контакте с представителями первой и второй субкультур. При этом скорость роста численности меценатов пропорциональна численности участников обеих субкультур (множитель ![]() в первом слагаемом третьего уравнения), но эта поддержка ограничена (множитель
в первом слагаемом третьего уравнения), но эта поддержка ограничена (множитель ![]() в первом слагаемом третьего уравнения (4)).
в первом слагаемом третьего уравнения (4)).
Случай отсутствия меценатов. В этом случае, поскольку ![]() , система уравнений (4) принимает вид
, система уравнений (4) принимает вид
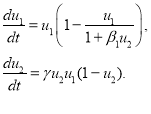
Стационарная точка этой системы уравнений ![]() ,
, ![]() устойчива. То есть в этом случае первая субкультура при поддержке второй субкультуры создаст на
устойчива. То есть в этом случае первая субкультура при поддержке второй субкультуры создаст на ![]() образов больше, чем без ее поддержки.
образов больше, чем без ее поддержки.
Случай отсутствия второй субкультуры. В этом случае система уравнений (4) принимает вид
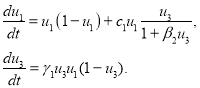
Стационарная точка этой системы уравнений
![]() ,
, ![]()
будет устойчивой. И поддержка меценатов позволит первой субкультуре создать дополнительно ![]() образов.
образов.
Таким образом, если ![]() , то вторая субкультура оказывает большее влияние на первую, чем меценаты. В противном случае более существенным является вклад меценатов.
, то вторая субкультура оказывает большее влияние на первую, чем меценаты. В противном случае более существенным является вклад меценатов.
Общий случай. Второе уравнение в (4) в окрестности точки
![]() ,
, ![]() ,
, ![]()
с точностью до величин второго порядка малости принимает вид
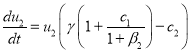 .
.
Отсюда следует, что ![]() в окрестности этой стационарной точки будет возрастающей функцией при выполнении неравенства
в окрестности этой стационарной точки будет возрастающей функцией при выполнении неравенства 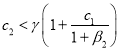 . Поэтому это неравенство является необходимым условием существования стационарной точки, в которой
. Поэтому это неравенство является необходимым условием существования стационарной точки, в которой ![]() ,
, ![]() ,
, ![]() . То есть в этом случае вторая субкультура будет оказывать поддержку первой совместно с меценатами.
. То есть в этом случае вторая субкультура будет оказывать поддержку первой совместно с меценатами.
На рис. 2 для случая ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() отражено влияние параметра
отражено влияние параметра ![]() на стационарное значения
на стационарное значения ![]() при
при ![]() и влияние параметра
и влияние параметра ![]() на стационарное значение
на стационарное значение ![]() при
при ![]() . На рис. 3 отражена зависимость
. На рис. 3 отражена зависимость ![]() при
при ![]() и
и ![]() при
при ![]() . Пунктирная линия соответствует логистической зависимости.
. Пунктирная линия соответствует логистической зависимости.
Как следует из полученных результатов в рамках рассмотренной модели при малой численности второй субкультуры большее влияние на начальном этапе взаимодействия трех субкультур на первую субкультуру оказывает субкультура меценатов. По мере роста численности второй субкультуры ее поддержка первой субкультуры становится более значимой, чем поддержка меценатов (рис. 2). Сама поддержка становится заметной только спустя некоторое время (рис. 3).
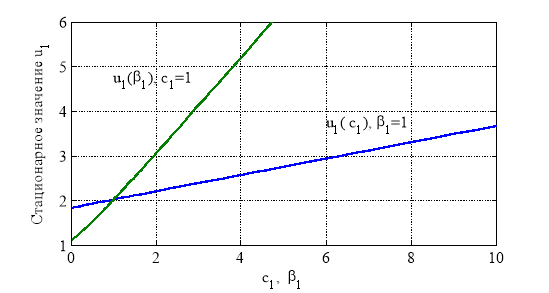
Рис. 2
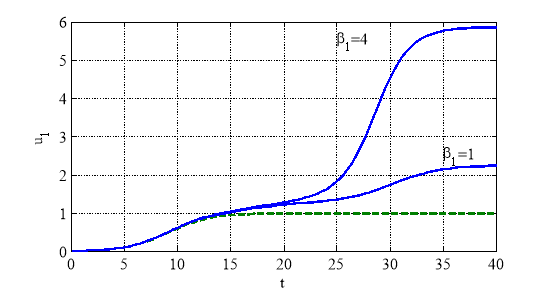
Рис. 3
Заключение. Предложенная модель трех взаимодействующих субкультур, разработанная на основе анализа поддержки художника К. П. Брюллова со стороны творческих субкультур писателей, архитекторов, артистов, меценатов на протяжении всей его жизни, позволяет оценить влияние внешних факторов на скорость роста созданных в субкультуре произведений. Не менее значимым является вывод о необходимость организации субкультур, поддерживающих друг друга в творческом поиске.
Литература:
- Амирханов, А. Ю. Духовность общества и власти — антагонизм или симбиоз? // Государственная служба. — 2011. — № 1. — С. 116–117.
- Андреев, В.В., Васильева Е. Б., Суконкина А. М. Попытка построения математических моделей для прогнозирования динамики социально-экономических систем // Вестник Чувашского университета. — 2006. — № 6. — С. 333–339.
- Ацаркина, Э. Н. Брюллов. М.: Искусство. 1963. — 536 с.
- Базыкин А. Д. Нелинейная динамика взаимодействующих популяций. Москва-Ижевск: Институт компьютерных технологий, 2003. — 368 с.
- Бехтиева, Е. В. Пейзаж романтизма в творческом наследии Карла Брюллова // Искусствознание. — 2015. — Т. 1. — № 1–2-1. — С. 308–323
- Бобриков, А. А. Искусство толпы. «Последний день Помпеи» Карла Брюллова и рождение массовой куль туры // Вестник Санкт-Петербургского государственного университета технологии и дизайна. Серия 2: Искусствоведение. Филологические науки. — 2011. — № 4. — С. 3–5.
- Брюллов, Карл Павлович (1799–1852), о нем. Воспоминания князя Григория Григорьевича Гагарина о Карле Брюллове. К 100-летию со дня рождения Брюллова. 1799–1899. СПб, 1900.
- Леонтьева, Г. К. Карл Брюллов: живопись, графика. Л.: Аврора, 1990. — 223 с.
- Горыня, Е.В., Колпак Е. П. Математические модели поиска экологической ниши // В сборнике: Устойчивость и процессы управления Материалы III международной конференции. — 2015. — С. 469–470.
- Демидова, Д.А., Алферов Г. В., Колпак Е. П., Смирнова Т. Е. Нелинейный процесс взаимодействия между коррумпированной фирмой и отделом по борьбе с коррупцией // Проблемы механики и управления: Нелинейные динамические системы. — 2015. — № 47. — С. 17–31.
- Джулиани, Р. Карл Брюллов и капризы его итальянской славы // Мир романтизма. — 2000. — № 3 (27). — С. 104–106.
- Екимов, А. В., Жабко А. П., Смирнов Н. В. Матричный анализ эргодических полу марковских процессов // Вестник Санкт-Петербургского университета. Серия 10. Прикладная математика. Информатика. Процессы управления. — 2004. — № 1–2. — С. 16–29.
- Жаткин, Д. Н., Круглова Т. С. Вальтер Скотт и Брюлловы // Мир науки, культуры, образования. — 2013. — № 3 (40). — С. 232–234
- Исланова, Ю. Р. Анатолий Демидов и Карл Брюллов: творческий союз или выгодное сотрудничество? // Вопросы культурологии. — 2013. — № 7. — С. 83–87.
- Камачкин, А. М., Старков В. Н., Степенко Н. А. Математическая модель загрязнения океанических вод // Вестник Тамбовского университета. Серия: Естественные и технические науки. — 2015. — Т. 20. — № 2. — С. 475–479.
- Колесин, И. Д. Принципы моделирования социальной самоорганизации: Учебное пособие. СПб.: Издательство Лань, 2013. — 388 с.
- Колпак, Е. П., Бронникова А. И., Полежаев В. Ю. Математическая модель стачечного движения в России в начале XX века // Молодой ученый. — 2015. — № 3 (83). — С. 4–15.
- Колпак, Е. П., Габриелян Л А., Бронникова А. И., Крылова В. А. О математических моделях симбиоза // Молодой ученый. — 2015. — № 4 (84). — С. 6–14.
- Колпак, Е. П., Горыня Е. В., Крылова В. А., Полежаев Д. Ю. Математическая модель конкуренции двух популяций на линейном ареале // Молодой ученый. — 2014. — № 12 (71). — С. 12–22.
- Колпак, Е. П., Матвеева И. А. О библиотеках. Санкт-Петербург. 2004.
- Колпак, Е. П., Скороходова Т. В. Математическая модель роста числа учащихся в средней и высшей школах России // В сборнике: Синергетика в естественных науках. Восьмые Курдюмовские чтения материалы Международной междисциплинарной научной конференции с элементами научной школы для молодежи. Ответственный редактор: Лапина Г. П. — 2012. — С. 274–275.
- Колпак, Е. П., Горыня Е. В. Математические модели «ухода» от конкуренции // Молодой ученый. — 2015. — № 11. — С. 59–70.
- Колпак, Е. П., Селицкая Е. А., Габриелян Л. А. Математическая модель коррупции в системе «власть — общество» // Молодой ученый. — 2015. — № 10 (90). — С. 9–16.
- Колпак, Е. П., Французова И. С., Кувшинова К. В. Народное здравие в костромской губернии в конце XIX века // Приволжский научный вестник. — 2016. — № 2 (54). — С. 91–100.
- Конради, П. Карл Брюллов. (1799–1852). Биографический очерк П. Конради. Киев-Харьков, Южно-рус. кн-во Ф. А. Иогансона, 1899.
- Корнилова, А. В. А. С. Пушкин и К. П. Брюллов. Интерпретация воспоминаний современников // Вестник Санкт-Петербургского государственного университета культуры и искусств. — 2011. — № 1. — С. 171–176.
- Коробицын, В. В., Фролова Ю. В. Математическая модель развития этнических групп // Математические структуры и моделирование. — 2008, — № 18, — С. 31–42.
- Крылова, В. А., Колпак Е. П., Сыромолотова К. И., Воротова Т. А. Математические модели формирования спортивных групп // Молодой ученый. — 2015. — № 8 (88). — С. 10–19.
- Куижева, С. К. Уравнение Кортевега-де Фриза и математические модели в социально-экономических системах // Вестник Адыгейского государственного университета. Серия 4: Естественно-математические и технические науки. — 2015. — № 1 (154). — С. 20–26.
- Матвиевская, Г. П. «Мне жаль, что я не отец ваш...» В. А. Перовский и братья Брюлловы. Гостиный Двор. — 2015. — № 50. — С. 277–292.
- Машковцев, Н., К. П. Брюллов в письмах, документах и воспоминаниях современников. М.: изд.-во Акад. художеств СССР, 1961. — 318 с.
- Миндлин, Ю. Б., Колпак Е. П., Балыкина Ю. Е Проблемы использования кластеров в Российской Федерации // Вестник НГУЭУ. — 2014. — № 1. — С. 22–32.
- Миндлин, Ю. Б., Колпак Е. П., Гасратова Н. А. Отличительные признаки кластеров и практика их применения в России // Политика и общество. — 2015. — № 5. — С. 666–675.
- Мирошниченко, Ю. П. Симбиоз массовой и элитарной культур, как неизбежный процесс эпохи новых технологий // Актуальные проблемы гуманитарных и естественных наук. — 2014. — № 12–2. — С. 319–322.
- Мокрицкий, А. Н. Воспоминания о Брюллове. СПб, 1855. — 184 с.
- Поташова, К. А. М. Ю. Лермонтов и К. П. Брюллов: жизненные и творческие связи // Молодой ученый. — 2012. — № 11. — С. 276–279.
- Поташова, К. А. Образ «Пылающего Везувия» в художественном мире А. С. Пушкина, М. Ю. Лермонтова, К. П. Брюллова // Филологические науки. Вопросы теории и практики. — 2015. — № 6–2 (48). — С. 133–137.
- Рамазанов, Н. Воспоминания о Карле Павловиче Брюллове. М., 1852. — 28 с.
- Смирнова, М. В., Колпак Е. П. Математическое моделирование снижения детской заболеваемости в России // В сборнике: Синергетика в общественных и естественных науках: Девятые Курдюмовские чтения Материалы Международной междисциплинарной научной конференции с элементами научной школы для молодежи. Ответственный редактор Лапина Г. П. 2013. С. 222.
- Сомов, А. И. Карл Павлович Брюллов и его значение в русском искусстве. СПб, тип. А. М. Котомина, 1876. — 29 с.
- Старкова, Н. В. Возрастная структура населения и повозрастная интенсивность рождений как факторы изменения уровня рождаемости в Ленинградской области // Вестник Санкт-Петербургского университета. Серия 7. Геология. География. — 2008. — № 3. — С. 98–106.
- Старкова, Н. В. Особенности демографического развития районов Ленинградской области // Вестник Санкт-Петербургского университета. Серия 7. Геология. География. — 2007. — № 4. — С. 87–97.
- Старкова, Н. В. Особенности социально-экономического развития приграничных муниципальных районов ленинградской области // В сборнике: Стратегия развития приграничных территорий: традиции и инновации Материалы международной научно-практической конференции. 2014. — С. 350–359.
- Старкова, Н. В. Современные особенности миграции населения Ленинградской области // В сборнике: Стратегия развития приграничных территорий: традиции и инновации Материалы II международной научно-практической конференции. 2015. — С. 173–180.
- Старкова, Н. В. Тенденции и факторы миграции в странах Европы // В сборнике: География и геоэкология на службе науки и инновационного образования материалы XI Международной научно-практической конференции, посвященной Всемирному Дню Земли и 100-летию заповедной системы России. 2016. — С. 154–157.
- Старкова, Н. В., Ложкинс А. Кластеризация стран Европы по демографическим признакам // Молодой ученый. — 2016. — № 9 (113). — С. 418–426.
- Balykina, Y. E., Kolpak E. P., Kotina E. D. Mathematical model of thyroid function // Middle East Journal of Scientific Research. — 2014. — Т. 19. — № 3. — С. 429–433.
- Ekimov, A. V.Qualitative analyses of attainability set of nonlinear controllable systems // В книге: 20th International Workshop on Beam Dynamics and Optimization (BDO) IVESC-ICEE-ICCTPEA-BDO-2014. Edited by: D. A. Ovsyannikov. 2014. — С. 49.
- Murray, D. D. Mathematical biology. N. Y. Springer, 2002. — 551 p.
- Pronina, Y. G. Analytical solution for decelerated mechanochemical corrosion of pressurized elastic-perfectly plastic thick-walled spheres // Corrosion Science. — 2015. — Т. 90. — С. 161–167.
- Sedova, O., Pronina Y. Generalization of the Lamé problem for three-stage decelerated corrosion process of an elastic hollow sphere // Mechanics Research Communications. — 2015. — Т. 65. — С. 30–34.
- Shiryaev, D. V., Litvinenko I. L., Rubtsova N. V., Kolpak E. P., Blaginin V. A., Zakharova E. N. Economic clusters as a form of self-organization of the economic system // International Journal of Economics and Financial Issues. — 2016. — Т. 6. № S1. — С. 284–288.
- Starkov, V. N., Stepenko N. A. Simulation of particle motion in the given speed fields // В сборнике: 2015 International Conference «Stability and Control Processes» in Memory of V. I. Zubov (SCP) 2015. С. 75–77.
- Zhukova, I.V., Kolpak E. P., Balykina Y. E. Mathematical model of growing tumor Applied Mathematical Sciences. — 2014. — Т. 8. — № 29–32. — С. 1455–1466.







