В статье с метрологической точки зрения рассмотрен процесс обучения измерительных систем на базе нейронных сетей. Выделены критерии показателей качества обучения, достоверности результата. Рассмотрены варианты классификации погрешности обучения с точки зрения классической метрологии.
Ключевые слова: нейронная сеть, измерительная система, метрология, качество обучения, погрешности обучения, классификация погрешностей
На данный момент не существует достаточного полного и универсального системотехнического и метрологического описания работы НС. Основываясь на экспериментальных данных можно сказать, что перспективы применения нейросетевых измерительных систем на базе нейронных сетей (ИС/НС) для анализа многопараметрических измерений очевидны. Но проблема корректной оценки метрологических характеристик таких измерений вызывает особую сложность в связи с большим количеством факторов, влияющих на погрешность измерений.
Выбор структуры НС осуществляется в соответствии с особенностями и сложностью задачи. Вопрос о необходимых и достаточных свойствах сети для решения того или иного рода задач представляет собой целое направление нейрокомпьютерной науки. В данной работе мы рассмотрим с метрологической точки зрения процесс обучения НС, практически не затрагивая выбор оптимальной архитектуры и совсем не останавливаясь на инструментальных погрешностях конкретных вариантов исполнения НС.
Типы НС обладают общими чертами, несмотря на существенные различия. Во-первых, основу каждой НС составляют относительно простые, в большинстве случаев — однотипные, элементы (ячейки), имитирующие работу нейронов мозга. Каждый нейрон характеризуется своим текущим состоянием по аналогии с нервными клетками головного мозга, которые могут быть возбуждены или заторможены.
Текущее состояние нейрона определяется, как взвешенная сумма его входов:
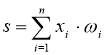 .
.
Выход нейрона есть функция его состояния: y = F(s).
Нелинейная функция F называется активационной и может иметь различный вид.
Выбор структуры НС осуществляется в соответствии с особенностями и сложностью задачи. Для решения некоторых отдельных типов задач уже существуют оптимальные варианты на сегодняшний день. Если же задача не может быть сведена ни к одному из известных типов, разработчику приходится решать сложную проблему синтеза новой конфигурации. При этом он руководствуется несколькими основополагающими принципами:
- возможности сети возрастают с увеличением числа ячеек сети, плотности связей между ними и числом выделенных слоев;
- введение обратных связей наряду с увеличением возможностей сети поднимает вопрос о динамической устойчивости сети;
- сложность алгоритмов функционирования сети (в том числе, например, введение нескольких типов синапсов — возбуждающих, тормозящих и др.) также способствует усилению мощи НС.
Процесс функционирования НС зависит от величин синоптических связей, поэтому, задавшись определенной структурой НС, отвечающей какой-либо задаче, разработчик сети должен найти оптимальные значения всех переменных весовых коэффициентов (некоторые синоптические связи могут быть постоянными). Этот этап называется обучением НС, и от того, насколько качественно он будет выполнен, зависит способность сети решать поставленные перед ней проблемы во время эксплуатации. На этапе обучения, кроме параметра качества подбора весов, важную роль играет время обучения. Как правило, эти два параметра связаны обратной зависимостью и их приходится выбирать на основе компромисса.
Существует великое множество различных алгоритмов обучения, которые, однако, делятся на два больших класса: детерминистские и стохастические. В первом из них подстройка весов представляет собой жесткую последовательность действий, во втором — она производится на основе действий, подчиняющихся некоторому случайному процессу.
Процесс обучения требует корректной оценки качества, достоверности результата, оценки возможных погрешностей. Одним из способов получения такой оценки является тестирование примеров.
Тестирование примеров нейросетью может проводиться с различными целями:
- Проверка того, как обучилась нейросеть;
- Решение конкретных задач;
- Моделирование.
В первом случае осуществляется тестирование выборки с заранее известными ответами примеров. Таким образом, можно проверить, правильно ли сеть определяет ответы примеров и насколько уверенно она это делает. Определенный сетью ответ примера сравнивается с заранее известным. Как правило, сначала тестирование проводится на той выборке, на которой сеть обучалась. Если сеть обучилась полностью, то при тестировании той же самой обучающей выборки ответы всех примеров будут определяться правильно. Гораздо больший интерес представляет тестирование аналогичной выборки с заранее известными ответами, но примеры, которой не участвовали в обучении сети. Неправильное определение ответов некоторых примеров может быть вызвано несколькими причинами:
– выборка, по которой обучалась нейросеть, составлена неграмотно, тенденциозно;
– обучающая выборка имеет недостаточное количество обучающих параметров и сеть не может найти закономерности между входными сигналами и ответами;
– при создании сети не оптимально были выбраны некоторые сетевые параметры, например, число нейронов, число тактов функционирования или характеристика сети.
– Задана неверная классификационная модель (при обучении нейросетей-классификаторов).
При решении конкретных задач сети подаются примеры, ответ которых неизвестен. В этой ситуации программа не может проверить правильность решения. Как уже говорилось, в отличие от большинства экспертных систем, работающих по четким правилам, решение задачи на основе опыта всегда имеет “нечеткий” характер. Поэтому кроме класса тестируемого примера, сеть вычисляет коэффициент уверенности в данном решении. Коэффициент уверенности зависит от заданного уровня надежности и рассчитывается по формуле:
![]()
где Max1 — ответ выходного нейрона, отвечающего за класс — «победитель»,
Max2 — ответ выходного нейрона, выдавшего следующий по максимальной величине сигнал, R — уровень надежности.
Из формуле видно, что уверенность сети зависит от того, насколько наибольший из выходных сигналов превышает второй по величине сигнал. Естественно, если КУ получается более 100 %, он приравнивается к этому числу. Из того, что в знаменателе правой части формулы стоит уровень надежности, следует, на первый взгляд, парадоксальный вывод: сеть, обученная лучше (уровень надежности больше), даст меньшую уверенность в ответе, чем сеть, обученная хуже. Однако при внимательном рассмотрении проблемы, становится ясно, что при тестировании примера первой сетью, выражение, стоящее в числителе, также будет больше (ответ одного нейрона будет намного больше ответа другого). Кроме того, КУ выражает все же уверенность конкретной сети, которая во многом зависит от того, насколько тестируемый пример близок к примерам, на которых обучалась эта сеть. Если пример отличается достаточно сильно, лучше обученная сеть будет и сомневаться больше, чем сеть с меньшим «опытом».
Один из показателей качества обучения — определение прогностической способности нейросети — состоит в подсчете процента правильно распознанных примеров. При сравнении качества обучения двух нейросетей, в случае, когда обе сети дают одинаковую прогностическую способность, можно подсчитывать средний процент уверенности при тестировании выборки. Поэтому среднее арифметическое процентных величин уверенностей, полученных при тестировании каждого примера, с заранее известным результатом, дает нам необходимый процент уверенности.
Из вышесказанного вытекает очень полезный для практики вывод. Изменяя в различных направлениях значения параметров примера и повторяя его тестирование, можно видеть, что и на сколько, нужно изменить, чтобы пример стал принадлежать к требуемому классу. Это может быть полезным для медицинской диагностики и прогнозирования. Предположим, что сеть обучена дифференцировать больных и здоровых людей по набору клинических параметров. Изменяя эти параметры, можно добиться, чтобы пример, определяемый как «больной», стал принадлежать классу «здоровый». Таким образом, станет ясно, какие клинические параметры подлежат изменению для улучшения состояния больного.
С точки зрения классической метрологии погрешности по одной из классификаций разделяются на методические и инструментальные. В классическом определении методических ![]() и инструментальных
и инструментальных ![]() погрешностей лежит представление полной погрешности в виде их суммы:
погрешностей лежит представление полной погрешности в виде их суммы: ![]() .
.
На основании канонического содержательного определения методической погрешности (погрешности метода) как составляющей полной погрешности, происходящей от несовершенства метода измерений, приходим к соотношению:
![]() ,
,
где R — характеризует преобразования без учёта инструментальной погрешности. Соответственно получаем:
![]() .
.
Разделение погрешностей на методические и инструментальные связано с уровнем и объемом априорной информации, используемой при описании измерительной процедуры и результатов измерения.
Рассмотрим варианты классификации погрешности обучения с точки зрения классической метрологии. С одной стороны, во многих задачах качество обучения оценить сложно, а зачастую и невозможно определить без проведения тестирования. В соответствии с метрологическим определением, с помощью эксперимента находятся инструментальные погрешности. Но с другой стороны, в классических измерениях методические погрешности вызываются: недостатками применяемого метода измерений, несовершенством теории физического явления и неточностью расчетной формулы, используемой для нахождения измеряемой величины.
Очевидно, что НС — весьма специфический инструмент измерений. Неточность классификации определяется: не корректным выбором структуры сети, не качественным обучением. Поэтому оценить погрешность без эксперимента можно только в случае относительно простых задач с заранее определенными алгоритмами. Авторы статьи считают, что погрешности выбора архитектуры и обучения следует все же относить к методическим погрешностям.
Другой вариант разделения погрешностей в метрологии — на статические и динамические погрешности. Погрешности обучения могут иметь различный характер. В задачах распознавания образов это скорее динамические погрешности, они зависят от входных параметров. В других видах измерений, погрешности архитектуры и обучения могут давать и статическую погрешность на определенных наборах входных параметров. Но на других параметрах, погрешность будет уже другой величины, если нейронная сеть хотя бы более или менее правильно подобрана и обучена. Тогда погрешности обучения следует считать динамическими.
Рассмотрим классификацию погрешностей обучения как систематические или случайные. Если не рассматривать инструментальные погрешности, вызванные ошибками при моделировании сети (которые на данном уровне развития микроэлектроники — минимальны и выходят за рамки данной работы), то результат решения одних и тех же примеров будут всегда повторяться. Если в процессе работы НС не происходит дополнительного обучения, то погрешности неоптимальной архитектуры и некачественного обучения будут проявляться на одних и тех же примерах. Т. е. в задачах классификации, те примеры, которые решались верно, будут неизменно достоверными, ошибочные — так и останутся не верными. Следовательно, погрешности обучения — статические. Однако во многих серьезных комплексах происходит постоянное обучение НС в процессе работы. В таком случае результаты измерений будут отличаться даже при одинаковых входных параметрах.
Таким образом, можно сделать вывод о том, что ИС/НС можно рассматривать с помощью методов классической метрологии. Однако эти системы весьма специфичны и имеют много отличий от классических формализованных измерительных систем.
Литература:
- Цветков Э. И. Основы математической метрологии, 2001 г. — 105с.
- Царегородцев В. Г. Определение оптимального размера нейросети обратного распространения через сопоставление средних весов синапсов // Материалы XIV Международной конференции по нейрокибернетике, Ростов-на-Дону, 2005. Т.2. — С.60–64.
- Рабинович С. Г. Погрешности измерений.-Л.: Энергия, 1978.- 262c.
- Новоселов О. Н, Фомин А. Ф. Основы теории и расчета информационно-измерительных систем.-2-е изд., перераб. и доп.- М.: Машиностроение, 1991.- 336 с.
- Цапенко М. П. Измерительные информационные системы: структуры и алгоритмы, системотехническое проектирование.: учеб. Пособие для вузов.- 2-е изд., перераб и доп.- М.: Энергоатомиздат, 1985.-438c.
- Обучение нейронной сети. Алгоритм обратного распространения ошибок. http://microtechnics.ru/obuchenie-nejronnoj-seti-algoritm-obratnogo-rasprostraneniya-oshibok/







