Данная статья посвящена методологии сравнения потоковых шифров. В статье рассматриваются потоковые шифры и их основные параметры. На основе этих параметров предлагается методика сравнения данных шифров, а также приводится пример применения данной методики к существующим и новым потоковым шифрам. На основании проведённого анализа делается вывод о том, какой из сравниваемых шифров наиболее предпочтителен для использования в криптографических системах.
Введение
В настоящее время в связи с развитием информационных технологий, связанных с передачей информации через Интернет, продолжается бурное развитие программного обеспечения, которое позволяет обмениваться информацией. Перед разработчиками данных программ встают такие проблемы как обеспечение секретности и целостности передаваемой информации.
Одним из решений данной проблемы является использование шифров, в частности потоковых шифров. Этот способ шифрования характеризуется тем, что отправитель и получатель знают ключ, который используется как для создания шифрованной последовательности из передаваемой информации, то есть для шифрования данных, так и для обратной операции расшифрования зашифрованной последовательности.
На данный момент существует множество потоковых шифров, поэтому перед разработчиками может возникнуть вопрос о том, какой из имеющихся шифров лучше подойдёт для их применения. Поэтому необходимо разработать критерии, по которым можно было бы сравнить различные потоковые шифры.
Потоковые шифры
Уже много лет человечество использует различные способы шифрования информации. Впрочем, на первых этапах развития письменности не было необходимости в особом кодировании сообщений, ведь уровень грамотности был очень низок. Лишь спустя долгое время, вместе с развитием общества и способов письменности, появилась нужда в том, чтобы сохранить секрет передаваемой информации.
Одним из известнейших первых шифров является, так называемый, шифр Цезаря. Основной идея шифра заключается в том, что каждая буква в сообщении заменяется другой буквой того же алфавита, которая отстоит на заданное число позиций от заменяемой буквы. В частности, если взять значение цикличного сдвига позиции равным 3, то в латинском алфавите буква A будет заменена на D, B на E, …, Z на C. Своей цели такое преобразование достигает — полученный шифр невозможно прочесть. Однако, если сообщение достаточно длинное, то можно сопоставить буквы по частоте появления букв в незашифрованном тексте, к примеру, в русском языке наиболее распространённая буква — о, и для того, чтобы понять величину сдвига, необходимо лишь посчитать частоту появления букв, встречающуюся в зашифрованном тексте.
Существует три [1] способа устранения данной уязвимости в шифре: омофонический, полиалфавитный и полиграммный шифр.
В омофоническом шифре происходит замена одной буквы исходного текста несколькими символов шифротекста. Распространённые буквы шифруются большим количеством символов, нежели редко встречающиеся. Каждый раз при кодировании буквы, случайно выбирается один из соответствующих ей символов.
В полиалфавитном шифре используются простые замены для каждой буквы (например, цикличные сдвиги), но замены отличны для каждой буквы в соответствии с заранее обговорённым способом. Эти различия в заменах скрывают частоту появления букв исходного текста.
В полиграммном шифре происходит замена блоков букв исходного текста на соответственные блоки шифротекста. Такой способ замены скрывает частоту появления букв в исходном тексте, а блоки, если их размер достаточно велик, практически не повторяются, являя собой защиту от атак, основанных на избыточности в исходном тексте.
Как видно, каждый из трёх способов помогает скрыть частоту появления букв в тексте, защищая, таким образом, шифрованный текст от атак, связанных с использованием данной частоты. Впрочем, омофонические шифры не очень подходят для автоматического шифрования, что является причиной того, что в настоящее время они не распространены, в отличие от остальных двух способов. В настоящее время потомками полиалфавитных шифров являются потоковые шифры, а полиграммные — блочных шифров.
Обычно, потоковые шифры быстрее и проще в реализации, чем блочные, но всё зависит от конкретных алгоритмов реализации.
Рассмотрим подробнее способ превращения открытого текста, состоящего из n битов вида m1, m2, …, mn, в шифрованный текст, состоящий, соответственно, из битов с1, c2, …, cn. Генератор гаммы создаёт ключевой поток k1, k2, …, kn, который затем при помощи операции XOR (исключающее ИЛИ) побитово складывается с открытым текстом m1, m2, …, mn. Полученная последовательность и будет являться зашифрованным текстом с1, c2, …, cn, ci = miki, где i = 1..n. Операция расшифрования производится аналогичным образом: зашифрованный текст побитово складывается при помощи операции XOR с ключевым потоком, mi = ciki, где i = 1..n.
В случае если ключевая последовательность случайна и равна по длине шифруемому тексту, шифр взломать невозможно. Однако, на практике, шифруемое сообщение бывает очень велико, поэтому используют короткий ключ, который порождает псевдослучайную ключевую последовательность. В таком случае зашифрованный текст оказывается уязвим к атакам, связанным с псевдослучайностью ключа.
Последовательные биты ключевой последовательности генерируются на основе внутреннего состояния генератора. Это состояние может быть изменено двумя способами:
‒ независимо от открытого или зашифрованного текста, в таком случае шифр называется синхронным;
‒ на основе предыдущих битов зашифрованного текста, в таком случае шифр называется самосинхронизирующимся.
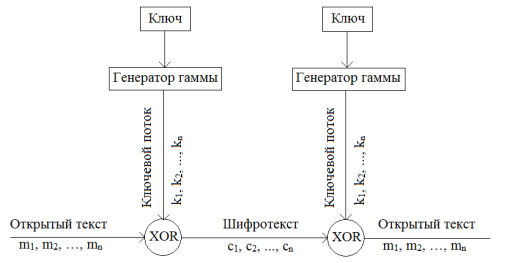
Рис. 1. Принцип работы синхронных потоковых шифров
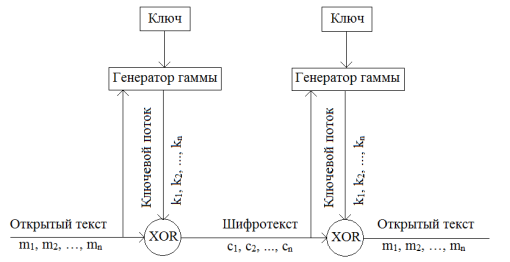
Рис. 2. Принцип работы самосинхронизирующихся потоковых шифров
При использовании синхронного потокового шифра, отправитель и получатель должны быть синхронизированы, то есть у них должен быть один и тот же ключ, для корректного расшифрования. Синхронизация прекращается в случае, если из зашифрованного текста были удалены элементы, или же, наоборот, в зашифрованный текст были добавлены дополнительные элементы. Для восстановления синхронизации могут быть использованы такие способы, как новая инициализация, расположение равномерно распределённых по зашифрованному тексту маркеров или подбор возможных сдвигов в ключевом потоке (если исходный текст достаточно избыточен). При использовании самосинхронизирующихся потоковых шифров расшифрование зависит только от определённого числа предшествующих символов зашифрованного текста. Следовательно, можно корректное расшифрование автоматически восстанавливается после потери синхронизации ценой определённого числа ошибочных символов исходного текста.
Один и тот же ключ в потоковых шифрах всегда создаёт один и тот же ключевой поток, поэтому длительное использование одного ключа приводит к уязвимости. Эту проблему можно решить посредством периодической смены ключа, но при таком способе появляются издержки, связанные с передачей ключей. Другой способ решения проблемы — использование векторов инициализации.
Вектор инициализации — случайная величина, изменяющаяся при каждой новой сессии работы шифра. [4] Вектор инициализации смешивается с ключом для формирования эффективного ключа в предстоящей сессии работы шифра, называемого сессионным ключом. Различные сессионные ключи генерируют различные ключевые последовательности, даже если используется один и тот же ключ в различных сессиях.
Исходя из вышеизложенного, можно заключить, что потоковые шифры могут сравнивать по их техническим характеристикам, то есть тем, которые связаны с производительностью данного шифра (например, используемая длина ключа), а также по вычислительной сложности существующих атак на шифр.
Технические характеристики
Данный вид характеристик характеризуется тем, что величины указываются в технической документации, сопутствующей описанию алгоритма шифрования. Рассмотрим технические характеристики потоковых шифров, которые могут быть использованы в качестве сравнительных величин:
‒ Длина эффективного ключа. Данная характеристика важна тем, что в зависимости от области применения, на используемый шифр накладываются ограничения, связанные с ГОСТ. Измеряется в битах.
‒ Длина вектора инициализации в битах.
‒ Скорость обработки 1 байта открытого текста, измеряется в количестве тактовых сигналов микропроцессора, обрабатывающего данные в соответствие с алгоритмом. На разных микропроцессорах может отличаться, поэтому для разных шифров следует проводить измерения для одного и того же микропроцессора.
Последняя величина может быть не указана явно, но, имея в распоряжении алгоритм, её можно довольно просто вычислить.
Также важной характеристикой является стойкость к существующим атакам. В случае, если для шифра в настоящее время не найдено зависимостей в формирующейся выходной последовательности, необходимо указывать полный перебор.
Сравнение некоторых шифров
В таблице, представленной ниже, приводится пример сравнения потоковых шифров по предложенным характеристикам. Сравниваемые шифры — RC4, Salsa20, HC-256 и SOSEMANUK.
Таблица 1
Cравнение шифров
|
Наименование |
Дата создания |
Длина ключа, бит |
Вектор инициализации, бит |
Скорость обработки 1 байта текста, число тактовых сигналов |
Наиболее значимые атаки |
Вычислительная сложность атаки |
|
RC4 |
1987 |
8–2048, Обычно 40–256 |
нет |
7 |
Флурер-Мантин-Шамир [5] |
213 |
|
Salsa20 |
2004 |
128, 256 |
128 |
11,84 |
Метод вероятностных нейтральных бит [6] |
2251 |
|
HC-256 |
2004 |
256 |
256 |
4 |
Только полный перебор |
2256 |
|
SOSEMANUK |
2004 |
128 |
128 |
27,1 [11] |
eSTREAM [10] |
2224 |
|
Espresso |
2015 |
128 |
95 |
8 |
Time-memory-data trade-off [12] |
2168 |
|
Fruit |
2016 |
80 |
70 |
8 |
Только полный перебор |
280 |
Данные шифры выбраны неслучайно, шифр RC4 на протяжении последних двух десятилетий остаётся одним из самых широко используемых потоковых шифром в мире. Остальные же шифры стали финалистами конкурса eSTREAM, который проводила организация EUECRYPT. [7] Целью конкурса было определить шифры, подходящие для широкого применения. Отдельно выявлялись шифры, подходящие для программной и для аппаратной реализации. Шифры Salsa20, HC-256 и SOSEMANUK являлись финалистами конкурса для шифров с программной реализацией. Шифры Espresso и Fruit выбраны как наиболее актуальные на момент написания статьи потоковые шифры, которые были спроектированы для аппаратного использования. Ввиду этого факта, для измерения скорости обработки одного байта исходного текста, мне было необходимо самостоятельно выполнить программную реализацию шифров Espresso и Fruit.
Два фактора: давнее создание и широкое распространение повлияли на то, что RC4 является более изученным, чем остальные шифры. Этим можно объяснить его относительно низкую стойкость по сравнению с остальными шифрами.
Данные по скорости обработки текста приведены для процессора Pentium 4 Willamette.
Выводы
В данной работе был проведён общий обзор потоковых шифров: было дано их определение, приведено краткое описание принципа работы, а также выделены 2 типа потоковых шифров синхронные и самосинхронизирующиеся. Для потоковых шифров были определены характеристики, по которым можно проводить их сравнение.
Следующие характеристики были выделены, как наиболее определяющие: длина эффективного ключа, длина вектора инициализации и скорость обработки 1 байта открытого текста. Также, было предложено сравнивать самые эффективные из известных атак на шифры.
Таким образом, были получены характеристики, позволяющие получить наглядное сравнение различных потоковых шифров между собой. Методика сравнения заключается в получении данных характеристик для сравниваемых шифров, и в сопоставлении полученных характеристик между собой. А также на примере шести (RC4, HC-256, Salsa20, SOSEMANUK, Espresso и Fruit) шифров представлен данный сравнительный анализ.
На основе полученных данных можно заключить, что наиболее быстродействующим и надёжным является шифр HC-256, однако, высокую надёжность можно объяснить низкой изученностью данного шифра. Принимая во внимание этот факт, наиболее приемлемым для использования можно назвать шифр Salsa20, который, несмотря на относительно низкое быстродействие, всё же имеет высокую надёжность, подтверждённую исследованиями. Наименее желательным для использования шифром можно считать RC4, поскольку относительно высокое быстродействие и простота реализации не могут компенсировать относительно низкую криптографическую стойкость.
Литература:
- A. Klein. StreamCiphers. — London. — Springer-Verlag, 2013.
- T.D. B. Weerasinghe. An Effective RC4 Stream Cipher. Available at: http://eprint.iacr.org/2014/171.pdf, accessed 17.07.2016.
- Рябко Б. Я., Фионов А. Н. Криптографические методы защиты информации. — Москва. — Издательство Горячая Линия-Телеком, 2005.
- S. Maitra, G. Paul. RC4 Stream Cipher and Its Variants. — Boca Raton. — Taylor & Francic Group, 2012.
- S. Fluhrer, I. Mantin, A. Shamir. Weaknesses in the Key Scheduling Algorithm of RC4. Available at: http://www.crypto.com/papers/others/rc4_ksaproc.pdf, accessed 02.09.2016.
- J. P. Aumasson, S. Fisher, A. Khazaei, W. Meier and C. Rechberger. New Feature of Latin Dances: Analysis of Salsa, ChaCha, and Rumba. Available at: http://cr.yp.to/rumba20/newfeatures-20071218.pdf, accessed 02.09.2016.
- eSTREAM: the ECRYPT Stream Cipher Project. Available at: http://www.ecrypt.eu.org/stream/, accessed 03.09.2016.
- Погорелов Б. А., Сачков В. Н. Словарь криптографических терминов. — Москва. — Издательство МЦНМО, 2006.А
- D. Boneh, V. Shoup. A Graduate Course in Applied Cryptography. Available at: https://crypto.stanford.edu/~dabo/cryptobook/draft_0_2.pdf, accessed 03.09.2016
- Y. Tsunoo, T. Saito, M. Shigeri, T. Suzaki, H. Ahmadi, T. Eghlidos and S. Khazaei. Evaluation of SOSEMANUK With Regard to Guess-and-Determine Attacks. Available at: http://www.ecrypt.eu.org/stream/papersdir/2006/009.pdf, accessed 04.09.2016
- C. Berbain, O. Billet, A. Canteaut, N. Courtois, H. Gilbert, L. Goubin, A. Gouget, L. Granboulan, C. Lauradoux, M. Minier, T. Pornin and H. Sibert. Sosemanuk, a fast software-oriented stream cipher. Available at: http://www.ecrypt.eu.org/stream/ciphers/sosemanuk/sosemanuk.pdf, accessed 06.09.2016.
- E. Dubrova and M. Hell. Espresso: A Stream Cipher for 5G Wireless Communication Systems. Available at: https://eprint.iacr.org/2016/241.pdf, accessed 19.09.2016.
- V. A. Ghafari, H. Hu and C. Xie. Fruit: Ultra-Lightweight Stream Cipher with Shorter Internal State. Available at: https://eprint.iacr.org/2016/355.pdf, accessed 19.09.2016.







