В этой статье представлен вашему вниманию обзор алгоритмов преобразования Фурье и их применение при анализе звуковой информации. В статье представлены несколько конкретных реализаций преобразования Фурье, их анализ, а также накладываемые ограничения. В заключении был сделал вывод о возможности применения этих алгоритмов в различных условиях.
В последние годы инженеры-разработчики электронной аппаратуры, инженеры-проектировщики помещений, звукорежиссеры и люди других профессий, так или иначе связанных с обработкой звуковой информации, большое внимание качеству записываемой, хранимой и обрабатываемой звуковой информации. Одним из критериев качества звуковой информации является спектр сигнала, для анализа которого сложились устойчивые методики, некоторые из которых будут освещены в данной статье.
Преобразование Фурье
При анализе звуковой информации одним из наиболее важных параметров исходного звукового сигнала является его спектр. Спектр сигнала — это результат разложения сигнала на более простые в базисе ортогональных функций. В качестве разложения зачастую используется преобразование Фурье, качестве базисных функций спектра используют синусоидальные и косинусоидальные функции.
Преобразование Фурье (ℱ)— операция, ставящая в соответствие каждой функции действительного переменного f(x) её спектр или Фурье-образ ![]() :
:
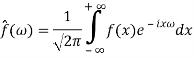 (1)
(1)
Виды преобразования Фурье:
– непериодический непрерывный или дискретный сигнал можно разложить в интеграл Фурье;
– непериодический дискретный сигнал можно разложить в интеграл Фурье;
– периодический непрерывный сигнал можно разложить в бесконечный ряд Фурье;
– периодический дискретный сигнал можно разложить в конечный ряд Фурье.
На практике, обычно, используется последний вид преобразований в связи с тем, что компьютеры способны работать с конечным набором данных.
Дискретное преобразование Фурье
Дискретное преобразование Фурье (ДПФ) (DiscreteFourierTransform, DFT) имеет вид:
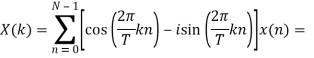
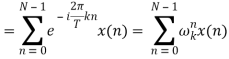 (2)
(2)
ДПФ ставит в соответствие N отсчетам сигнала x(n), где n = 0…N — 1, N отсчетов дискретного спектра X(k), при этом предполагается, что и сигнал, и спектр сигнала являются периодическими и анализируются на одном периоде повторения. В связи с тем, что вычисление ДФП требует ![]() умножений полиномов и вычислений синусов, использование данного алгоритма на практике может оказаться очень ресурсоемким.
умножений полиномов и вычислений синусов, использование данного алгоритма на практике может оказаться очень ресурсоемким.
Псевдокод метода, реализующего ДПФ, представлен ниже:
DFT(x[]):
N length[x]
for k 0 to N/2
ReX[k] 0
ImX[k] 0
for i 0 to N
ReX[k] ReX[k] + x[i]∙cos(2πik/N)
ImX[k] ImX[k] – (x[i]∙sin(2πik/N))
X[k] = ReX[k] + ImX[k]
returnX[]
Быстрое преобразование Фурье
Когда не хватает ресурсов для вычисления ДФП, переходят к быстрому преобразованию Фурье. В методе БПФ используются коэффициента полинома ![]() с четными и нечетными индексами, чтобы определить два новых полинома
с четными и нечетными индексами, чтобы определить два новых полинома ![]() и
и ![]() с четными и нечетными коэффициентами:
с четными и нечетными коэффициентами:
![]() (3)
(3)
В этом случае ![]() содержит все коэффициенты индексами (двоичное представление которых заканчивается цифрой 0), а
содержит все коэффициенты индексами (двоичное представление которых заканчивается цифрой 0), а ![]() содержит все коэффициенты с нечетными индексами (двоичное представление которых заканчивается цифрой 1), тогда спектр дискретного сигнала рассчитывается по формуле:
содержит все коэффициенты с нечетными индексами (двоичное представление которых заканчивается цифрой 1), тогда спектр дискретного сигнала рассчитывается по формуле:
![]() (5)
(5)
Таким образом, задача вычисления спектра сводится к следующим операциям:
-
вычислить два полинома
 и
и  , имеющие степень не выше n/2 d в точках
, имеющие степень не выше n/2 d в точках  ;
;
- вычислить спектр, объединив результаты, используя формулу (5).
Псевдокод метода, реализующего БПФ, представлен ниже:
nlength(x[])
if n = 1
then returnx[]
![]()
![]()
![]() 1
1
![]()
![]()
![]() recursiveFFT(
recursiveFFT(![]() )
)
![]() recursiveFFT(
recursiveFFT(![]() )
)
fork 0 to n/2 – 1
![]()
![]()
returna[]
Каждый вызов recursiveFFT, за исключением рекурсивных вызовов, занимает Θ(n), где n — длина исходного набора дискретных отсчетов. В таком случае, рекуррентное соотношение для временной сложности алгоритма выглядит следующим образом:
![]() (6)
(6)
Самым важным ограничением, при реализации БПФ является то, что число дискретных отсчетов n должно быть степенью двойки. В случае, если это условие не выполняется, анализируемый сигнал можно дополнить нулями до степени двойки.
Помимо «классического» алгоритма БПФ также существует множество его вариаций, основная идея которых также основывается на декомпозиции ДПФ до операций с отдельными точками и последующее объединение полученных результатов:
– БПФ по основанию 2 с прореживанием по времени, БПФ по основанию 2 с прореживание по частоте — в этих алгоритмах используется двоично-инверсная перестановка и умножения результатов укороченного ДПФ на поворотные коэффициенты;
– полифазное БПФ (polyphaseFFT) — алгоритм, позволяющий получить очень высокое разрешение по частоте, по сравнению с другими алгоритмами БПФ;
– алгоритм БПФ Кули-Тьюки (Cooley-TukeyFFTalgorithm) и д. р.
Практическая реализация
В учебных целях был разработан анализатор спектра на микроконтроллере AtmelATmega32–16PU с использованием LCD-дисплея 16х2 на базе контроллера HitachiHD44780 LCD. Было принято решение использовать алгоритм ДПФ для реализации данной задачи в связи со следующими аппаратными и программные ограничениями:
– использование LCD-дисплея 16x2 означает, что имеется возможность визуализировать спектр сигнала с 16 дискретными частотами;
– стек микроконтроллер AtmelATmega32–16PU состоит из двух 8-битных регистров, поэтому, использование алгоритмов БПФ не представляется возможным в связи с возможным переполнением стека из-за рекурсии;
– в качестве лингвистического обеспечения для разработки был выбран язык программирования — C. В связи с этим основным лингвистическим ограничением является невозможность передачи массива в качестве аргумента в функцию, а также возвращать результат вычислений в виде массива в явном виде. В связи с этим ограничением для передачи данных из массива в функцию используются указатели;
– для уменьшения количества вычислительных операций, в память микроконтроллера были записаны возможные значения углов, синусов и косинусов.
Ниже представлен фрагмент кода на языке C, реализующий ДПФ на микроконтроллере ATmega32:
void discrete_fourier_transform (int32_t *x, uint32_t *amp, int n)
{
int16_t degree;
int32_t re_x, im_x;
for (int i = 0; i < n / 2; i++) {
re_x = 0;
im_x = 0;
for (int j = 0; j < n; j ++) {
degree = (uint16_t)pgm_read_byte_near(degree_lookup + i*n + j)*2;
re_x += *(x + j) * (int16_t)pgm_read_word_near(cos_lookup + degree);
im_x += -*(x + j) * (int16_t)pgm_read_word_near(sin_lookup + degree);
}
*(amp + i) = sqrt(re_x * re_x + im_x * im_x);
}
}
В качестве входных аргументов данная функция принимает указатель на первый элемент массива X [], содержащий данные, полученные с АЦП микроконтроллера; указатель на первый элемент массива amp [], содержащий значения амплитуд; n- число измерений, нашем случае 32 точки достаточно т. к. накладывается ограничение дисплея. Макрос pgm_read_byte_near() позволяет считывать байт данных из программного пространства по заданному адресу, таким образом осуществляется доступ к записанным ранее значениям синусов и косинусов в памяти микроконтроллера.
Для проверки работоспособности разработанного анализатора спектра звуковой частоты был разработан экспериментальный стенд, структурная схема которого представлена на рисунке 1.
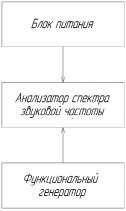
Рис. 1. Схема структурная экспериментального для анализатора спектра звуковой частоты
Весь экспериментальный стенд разделён на 3 блока: блок питания, анализатор спектра звуковой частоты, функциональный генератор. Питание для анализатора спектра звуковой частоты поступает от блока питания постоянного напряжение +12В. На вход анализатора спектра звуковой частоты поочередно подаются сигналы с функционального генератора с частотой не более 10кГц и амплитудой 0.3В...2.5В.
Для испытаний анализатора спектра звуковой частоты была разработана модель в программном комплексе «Proteus 8.1», а также собрано изделие. Результаты испытаний сравниваются между моделью и собранным изделием. Исследование осуществлялось при изменении частоты сигнала и его амплитуды.
Тест № 1 fс1 = 20Гц, fс2 = 588Гц, fс3 = 10кГц при Uc = 2.5В.
В тесте № 1 необходимо провести три измерения для сигнала с частотой fс1, затем для сигнала с частотой fс2, затем для сигнала с частотой fс3. Амплитуда сигнала во всех трех измерениях должна составлять Uс = 2.5В.
На рисунке 2 представлено сравнение результатов в моделирования в программном комплексе «Proteus 8.1» (слева) и результатов исследования тестового образца (справа) для fс1 = 20Гц, fс2 = 588Гц, fс3 = 10кГц (сверху вниз соответственно) при Uc = 2.5В.
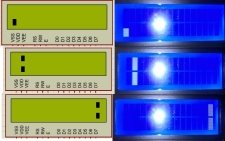
Рис. 2. Сравнение результатов моделирования (слева) и экспериментального исследования (справа) для теста № 1
Проведенный тест показывает спектр сигнала при максимальной амплитуде и граничных значениях частоты. В разработанном устройстве существует погрешность измерения спектра для сигнала с частотой fс < 588Гц.
Тест № 2 fс1 = 20Гц, fс2 = 588Гц, fс3 = 10кГц при Uc = 0.3В.
В тесте № 2 необходимо провести три измерения для сигнала с частотой fс1, затем для сигнала с частотой fс2, затем для сигнала с частотой fс3. Амплитуда сигнала во всех трех измерениях должна составлять Uс = 0.3В.
На рисунке 3 представлено сравнение результатов в моделирования в программном комплексе «Proteus 8.1» (слева) и результатов исследования тестового образца (справа) для fс1 = 20Гц, fс2 = 588Гц, fс3 = 10кГц (сверху вниз соответственно) при Uc = 0.3В.

Рис. 3. Сравнение результатов моделирования (слева) и экспериментального исследования (справа) для теста № 2
Проведенный тест показывает спектр сигнала при минимальной амплитуде и граничных значениях частоты.
Тест № 3 fс1 = 588Гц, fс2 = 1176Гц, при Uc = 2.5В.
В тесте № 3 необходимо провести три измерения для сигнала с частотой fс1, а затем для сигнала с частотой fс2. Амплитуда сигнала обоих измерениях должна составлять Uс = 2.5В.
На рисунке 3 представлено сравнение результатов в моделирования в программном комплексе «Proteus 8.1» (слева) и результатов исследования тестового образца (справа) для fс1 = 20Гц, fс2 = 588Гц (сверху вниз соответственно) при Uc = 2.5В.

Рис. 4. — Сравнение результатов моделирования (слева) и экспериментального исследования (справа) для теста № 3
Проведенный тест показывает, что разрешающая способность разработанного анализатора спектра звуковой частоты составляет 588Гц.
По результатам проведенных тестов, можно сделать вывод о том, что разработанная в программном комплексе «Proteus 8.1» модель, а также собранное изделие являются работоспособными.
Выводы
Были рассмотрены два алгоритма, реализующие преобразование Фурье — ДПФ и БПФ. Оба алгоритма могут применяться для анализа звукового сигнала; к достоинствам дискретного преобразования Фурье можно отнести простоту реализации, но главным его недостатком является большая временная сложность. ДПФ можно применять на небольших объемах дискретных, когда не требуется высокая дискретизация по частоте, однако, в настоящее время, ДФП применяется редко. БПФ и различные его вариации используются почти во всем оборудовании для анализа спектра сигнала, как отмечалось выше, это обусловлено тем, что временная сложность алгоритма ![]() , что позволяет использовать его в реальном времени. Основное ограничение — количество дискретных отсчетов n должно быть степенью двойки. Как отмечалось выше, анализируемый сигнал можно дополнить нулями. Побочными эффектами такого дополнения станут уменьшение амплитуды спектра и изменение фазовой компоненты, в связи с тем, что для спектрального анализа сигнала фазовая компонента не учитывается, таким приемом зачастую пользуются для увеличения дискретизации по частоте и по времени одновременно, а значения амплитуды поправляются, т. к. ее изменения вычисляемы. В учебных целях была разработана модель анализатора спектра звуковой частоты в программном комплексе «Proteus 8.1», а также собран анализатор спектра звуковой частоты. Были произведены экспериментальные исследования разработанной модели и собранного устройства, которые показали их работоспособность.
, что позволяет использовать его в реальном времени. Основное ограничение — количество дискретных отсчетов n должно быть степенью двойки. Как отмечалось выше, анализируемый сигнал можно дополнить нулями. Побочными эффектами такого дополнения станут уменьшение амплитуды спектра и изменение фазовой компоненты, в связи с тем, что для спектрального анализа сигнала фазовая компонента не учитывается, таким приемом зачастую пользуются для увеличения дискретизации по частоте и по времени одновременно, а значения амплитуды поправляются, т. к. ее изменения вычисляемы. В учебных целях была разработана модель анализатора спектра звуковой частоты в программном комплексе «Proteus 8.1», а также собран анализатор спектра звуковой частоты. Были произведены экспериментальные исследования разработанной модели и собранного устройства, которые показали их работоспособность.
Литература:
- Томас Кормен, Чарльз Лейзерсон, Рональд Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ, 2-е издание. Издательский дом «Вильямс», 2005г — стр. 926–954
- Зорич В. А. Математический анализ. — М.: Физматлит, 1984. — 544 с.
- Алексей Лукин. Введение в цифровую обработку сигналов (математические основы). Лаборатория компьютерной графики и мультимели, МГУ, 2007 стр. 16–22
- Электронный ресурс: Простыми словами о преобразовании Фурье / Хабрахабр http://habrahabr.ru/post/196374/
- Электронныйресурс: Atmel ATmega32 microcontroller datasheet / http:// http://www.atmel.com/Images/doc2503.pdf







