Описание нестационарных случайных процессов с помощью модели с переменными параметрами

Описание нестационарных случайных процессов спомощью модели спеременными параметрами

Андриянов Никита Андреевич, аспирант;

Дементьев Виталий Евгеньевич, кандидат технических наук, доцент;

Ульяновский государственный технический университет

В настоящей статье представлен алгоритм моделирования неоднородных случайных процессов, основанный на применении моделей с изменяющимися параметрами. При этом внимание уделяется моделям на основе базового набора возможных значений корреляционных параметров.

Ключевые слова: дважды стохастические модели, случайные процессы, авторегрессия

Часто реальные сигналы, будь то модулированная речь человека или результат аэросъемки земной поверхности, представляют собой сложные нестационарные во времени случайные процессы и поля (СП). Известные модели сигналов [1] не способны эффективно описывать присущие реальным данным свойства неоднородности (пространство) и нестационарности (время).

Чтобы решить указанную проблему, для адекватной передачи в модель отмеченных свойств предложено использовать смешанные модели [3–5, 7]. Чаще всего речь в этом случае идет о дважды стохастических моделях СП [2, 6, 8]. Это вызвано рядом причин. Во-первых, дважды стохастические модели достаточно просты с точки зрения математического описания. Во-вторых, данные модели относительно просто реализуются с помощью ЭВМ. В-третьих, такие модели могут описывать нестационарный во времени сигнал и могут быть использованы при решении широкого спектра задач цифровой обработки сигналов.

Очевидно, что незначительное увеличение вычислительных затрат при переходе к дважды стохастическим моделям не становится глобальным препятствием ввиду достаточно быстродействующей современной вычислительной техники. Кроме того, такие модели могут покрыть ряд задач описания сигналов, для которых могут удовлетворительно применяться авторегрессионные СП.

Однако большинство из предлагаемых дважды стохастических моделей требует случайной реализации корреляционных параметров. Создания устойчивых статистических связей в этом случае можно добиться на основе применения моделей с кратными корнями характеристических уравнений [9]. Альтернативным вариантом является задание базовых возможных значений корреляционных параметров и определение интервалов их действия.

,(1)

где — независимые гауссовы случайные величины с , ; — постоянная величина, характеризующая среднее значение коэффициента корреляции.

Тогда запишем выражение, определяющее корреляционные параметры в каждой точке

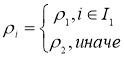,(2)

Модель (1) с учетом (2) позволяет формировать на одном сигнале области, которые значительно отличаются друг от друга по своим статистическим свойствам. При этом в (2) область необязательно должна быть непрерывной.

На графиках рис. 1 представлены: реализация дважды стохастической модели (1) с коэффициентами корреляции (2).

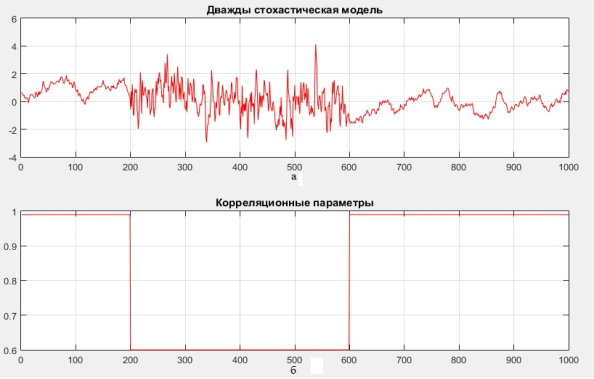
Рис. 1. Реализация дважды стохастической модели (а) и ее корреляционных параметров (б)

Таким образом, предложенный метод имитации неоднородных сигналов. Обобщение алгоритма на многомерный случай позволит в перспективе получать на изображениях, достаточно разнящиеся друг от друга объекты.

Литература:

1. Васильев К. К., Крашенинников В. Р. Статистический анализ изображений. — Ульяновск: УлГТУ, 2015. — 214 с.
2. Vasil'ev K. K., Dement'ev V. E., Andriyanov N. A. Doubly stochastic models of images // Pattern Recognition and Image Analysis (Advances in Mathematical Theory and Applications). 2015. Т. 25. № 1. С. 105–110.
3. Vasil'ev K. K., Dement'ev V. E., Andriyanov N. A. Application of Mixed Models for Solving the Problem on Restoring and Estimating Image Parameters // Pattern Recognition and Image Analysis (Advances in Mathematical Theory and Applications). 2016. Т. 26. № 1. С. 240–247.
4. Андриянов Н. А., Дементьев В. Е. Смешанные модели изображений на многомерных сетках // Актуальные вопросы технических наук в современных условиях. Сборник научных трудов по итогам международной научно-практической конференции. Санкт-Петербург, 2016. С. 9–12.
5. Андриянов Н. А., Дементьев В. Е. Восстановление сигнала с использованием смешанной АР-модели//Современные проблемы проектирования, производства и эксплуатации радиотехнических систем. 2014. № 1. С. 64–66.
6. Андриянов Н. А., Дементьев В. Е. Формирование временных последовательностей дважды стохастических моделей изображений // Сборник научных трудов по итогам 9-й Всероссийской научно-практической конференции "Современные проблемы проектирования, производства и эксплуатации радиотехнических систем". 2015. С. 89–93.
7. Андриянов Н. А. Программа имитации обычных и смешанных случайных полей // Современные тенденции в науке, технике, образовании. Сборник научных трудов по материалам Международной научно-практической конференции: в 3-х частях. 2016. Ч. 1, С. 38–40.
8. Васильев К. К., Дементьев В. Е., Андриянов Н. А. Цифровая обработка дважды стохастических моделей случайных полей // Молодой ученый. — 2016. — № 10. — С. 137–138.
9. Васильев К. К. Авторегрессии с кратными корнями характеристических уравнений // Радиотехника. 2014. № 11. С. 74–78.