В статье стандартными методами аналитической геометрии определяются высота различных точек и другие геометрические параметры внутри границы проектируемых открытых площадок размещения технологического оборудования для сбора, подготовки и транспорта нефтяной и газовой продукции по координатам этих точек в плане и координатам точек, определяющих положение плоскости площадки в пространстве, приводится компьютерная программа для их вычисления. Статья предназначена для специалистов нефтяной и газовой отраслей промышленности и строительных предприятий, для научных и инженерно-технических работников проектно-конструкторских организаций при проектировании новых, реконструкции и техническом перевооружении существующих объектов добычи газа, газового конденсата, нефти.
Ключевые слова: высота,координата, общее и векторное уравнение плоскости, общее, каноническое и параметрическое уравнения прямых, условия перпендикулярности прямой и плоскости в пространстве, ячейка
В соответствии с 5.3 СНиП 11–02 [1] при инженерно-геодезических изысканиях для строительства, в том числе, выполняются:
− сбор и обработка материалов инженерных изысканий прошлых лет, топографо-геодезических, картографических, аэрофотосъемочных и других материалов и данных;
− создание (развитие) опорных геодезических сетей (плановых сетей 3 и 4 классов и сетей сгущения 1 и 2 разрядов, нивелирной сети II, III и IV классов), а также геодезических сетей специального назначения для строительства;
− создание планово-высотных съемочных геодезических сетей;
− топографическая (наземная, аэрофототопографическая, стереофотограмметрическая и др.) съемка в масштабах 1:10000–1:200, включая съемку подземных и надземных сооружений;
− обновление топографических (инженерно-топографических) планов в масштабах 1:10000–1:200 и кадастровых планов в графической, цифровой, фотографической и иных формах;
− создание (составление) и издание (размножение) инженерно-топографических планов, кадастровых и тематических карт и планов, атласов специального назначения (в графической, цифровой и иных формах) и др.
При этом в соответствии с 5.10 СП 11–104–97 плановое положение пунктов опорной геодезической сети при инженерно-геодезических изысканиях для строительства следует определять методами триангуляции, полигонометрии, трилатерации, построения линейно-угловых сетей, а также на основе использования спутниковой геодезической аппаратуры (приемники GPS и др.) и их сочетанием [2].
Данные задачи могут быть решены с помощью различных систем автоматизированного проектирования (САПР), таких как: Credo Трансформ, Credo Dat, Credo Топоплан, Credo Нивелир, Credo Транскор — программы для инженерно-геодезических изысканий, землеустроительных и проектных работ, маркшейдерского обеспечения, землеустройства, кадастра, дорожно-транспортного строительства, Топоматик Robur — Геодезия — программа для обработки геодезических измерений, Топаз — топографический пакет землеустроителей, K-MINE — современная компьютерная разработка, позволяющая решать задачи геопространственного анализа данных различной сложности, GeoMax ZGP800, Геодезический калькулятор и другие. Эти программные продукты имеют относительно высокую стоимость и, обычно устанавливаются на стационарных компьютерах в различных проектных, строительных и других организациях.
Однако, при проектировании новых, реконструкции и техническом перевооружении уже существующих объектов добычи газа, газового конденсата, нефти возникает необходимость решения локальных задач, не требующих применения мощных вычислительных программ для автоматического проектирования, таких как, определение высоты различных точек (опор, штуцеров, свечей т. п.) и других геометрических параметров внутри границы проектируемых открытых площадок (например, на установках комплексной подготовки газа: площадок переключающей арматуры, аппаратов воздушного охлаждения, резервуарных парков, горизонтальных факельных установок и др. для размещения технологического оборудования в соответствии с нормативными значениями уклонов, направлений движения транспортируемых сред, взаимного расположения арматуры, фитингов, стыков и т. п.) по координатам х и у этих точек в плане и координатам точек, определяющих положение плоскости площадки в пространстве.
В связи возможностью возникновения ситуаций, когда использование мощных САПР затруднительно (например, в командировке и т. п.), а для принятия быстрого предварительного решения необходимо знание основных геометрических параметров различных точек внутри проектируемых площадок, целью настоящей работы является математическое определение некоторых геометрических значений площадок, а также написание компьютерной программы для их вычисления с помощью стандартного программного обеспечения Microsoft Office — программы Microsoft Excel.
Задача определения высоты Z различных точек строительных площадок, а также задача определения принадлежности (или не принадлежности) точки к известной плоскости и задача определения расстояния от точки до плоскости и другие решаются с помощью стандартных методов аналитической геометрии [3].
Известно, что плоскость может быть задана с помощью 3-х точек А(x0, y0, z0), В(x1, y1, z1), С(x2, y2, z2), не лежащих на одной прямой (рис.1), векторным уравнением плоскости в координатной записи:
![]()
![]()
![]()
![]() х–х0 х1–х0 х2–х0 х–х0EF
х–х0 х1–х0 х2–х0 х–х0EF
y–y0y1–y0y2–y0 = y–y0HK = (х–х0).H.N + (y–y0).M.F + (z–z0).E.K –
z–z0z1–z0z2–z0 z–z0MN
– (х–х0).M.K – (y–y0).E.N – (z–z0).H.F=0(1)
где E=х1–х0, F=х2–х0, H=y1–y0, K=y2–y0, M=z1–z0, N=z2–z0.
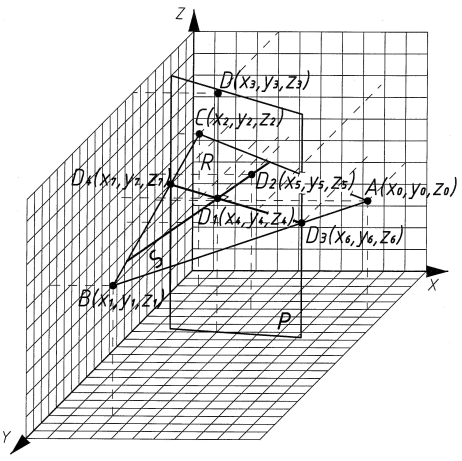
Рис. 1. Схема к определению геометрических параметров
После преобразования получим следующую запись уравнения плоскости АВС (плоскости S):
L.x + Q.y +U.z –W=0(2)
где L=(H.N–M.K), Q=(M.F–E.N), U=(E.K–H.F), W=(H.N–M.K).x0+(M.F–E.N).y0+(E.K–H.F).z0.
Для определения принадлежности (или не принадлежности) точки D(x3, y3, z3) плоскости АВС необходимо подставить координаты точки D в найденное уравнение (2) и проверить равняется ли оно нулю или нет.
Для определения координаты z4, при которой точка D1c координатами (x4, y4)в плане равными координатам (x3, y3) точки D (x4=x3, y4=y3), будет принадлежать плоскости АВС подставить координаты (x4, y4) точки D1 в уравнение (3), полученное в результате преобразования уравнения (2):
z4=(W — L.x4 — Q.y4)/U(3)
Расстояние по вертикали от точки D до плоскости АВС определится по формуле (4):
R= z3-z4(4)
Представляет интерес определение уравнений горизонтальной линии и линии наибольшего наклона плоскости к горизонту, проходящие через любую точку плоскости АВС, например, точку D1.
Так как D1 принадлежит плоскости АВС, то для нахождения уравнения горизонтальной линии необходимо найти координаты 2-й точки D2 (x5, y5, z5), которая принадлежала бы горизонтальной линии и одновременно плоскости АВС. Линия D1D2 — горизонтальная, поэтому z5=z4. Определив хmах=max{x0,x1,x2} и хmin=min{x0,x1,x2}, задавая любое значение х5 из X={хmах, хmin }, например х5=(хmах — хmin)/2, найдем y5 из уравнения плоскости (2):
y5=(W-L.x5-U.z5)/Q(5)
Тогда уравнение прямой в пространстве, проходящей через точки D1 (x4, y4, z4) и D2 (x5, y5, z5):
(x –x4) ̳ (y –y4) ̳ (z –z4)(6)
![]()
![]()
![]()
![]() (x5–x4) (y5–y4) (z5–z4)
(x5–x4) (y5–y4) (z5–z4)
Для нахождения уравнения линии наибольшего наклона плоскости, проходящей через точку D1 плоскости АВС, необходимо сначала найти уравнение плоскости Р, перпендикулярной D1D2. Т. к. нормальный вектор n плоскости Р совпадает с направляющим вектором а={А1, В1, С1} прямой D1D2, где А1=(x5–x4), В1=(y5–y4), C1=(z5–z4), и плоскость Р проходит через точку D1 (x4, y4, z4), то уравнение плоскости Р, заданное через координаты т. D1 и нормальный вектор n будет:
![]()
![]()
![]() A1.(x–x4)+B1.(y–y4)+C1.(z–z4)=0(7)
A1.(x–x4)+B1.(y–y4)+C1.(z–z4)=0(7)
После преобразования уравнения (7) получим:
A1.x+B1.y+С1.z –W1=0(8)
где W1=(A1.x4+B1.y4+C1.z4).
Уравнение прямой наибольшего наклона плоскости S к горизонту может быть получено как пересечение плоскостей S и Р:
![]() L.x + Q.y +U.z –W=0(9)
L.x + Q.y +U.z –W=0(9)
A1.x+B1.y+С1.z –W1=0
После решения системы уравнений (9) получим уравнение прямой D1D3:
(L+А1).x + (Q+В1).y +(U+С1).z –(W+W1)=0(10)
С целью определения точек пересечения линии наибольшего наклона плоскости S к горизонту, проходящую через т. D1, с периметром площади АВС, определим точки пересечения плоскости Р с прямыми АВ, ВС, АС. Для этого переведем канонические уравнения данных прямых в параметрические.
Каноническое уравнение прямой АВ:
(x –x0) ̳ (y –y0) ̳ (z –z0) ̳t1(11)
![]()
![]()
![]()
![]()
![]() (x1–x0) (y1–y0) (z1–z0) 1
(x1–x0) (y1–y0) (z1–z0) 1
Параметрическое уравнение прямой АВ:
х=х0+l1.t1, y=y0+m1.t1, z=z0+n1.t1(12)
где l1=х1–х0, m1=y1–y0, n1=z1–z0.
Подставив уравнения (12) в уравнение (8) получим параметр t:
(A1.x0+B1.y0+С1.z0 –W1)
![]() t1= – (13)
t1= – (13)
(A1.l1+B1. m1+С1. n1)
Подставляя параметр t1 в уравнения (12) получим точку D3 (x6, y6, z6) пересечения прямой АВ с плоскостью Р.
Аналогично находим параметрические уравнения прямых ВС и АС соответственно (14) и (15):
х=х1+l2.t2, y=y1+m2.t2, z=z1+n2.t2(14)
х=х0+l3.t3, y=y0+m3.t3, z=z0+n3.t3(15)
где l2=х2–х1, m2=y2–y1, n2=z2–z1 и l3=х2–х0, m3=y2–y0, n3=z2–z0.
Подставляя уравнения (14) в уравнение (8) получим соответственно параметры t2 и t3, аналогичные уравнению (13):
(A1.x1+B1.y1+С1.z1 –W1)
![]() t2= – (16)
t2= – (16)
(A1.l2+B1.m2+С1.n2)
(A1.x0+B1.y0+С1.z0 –W1)
![]() t3= – (17)
t3= – (17)
(A1.l3+B1.m3+С1.n3)
Подставляя параметры t2 и t3 в уравнения (14) и (15) соответственно получим точки D4 (x7, y7, z7) и D5 (x8, y8, z8)пересечения прямых ВС и АС с плоскостью Р.
Определив zmax=max{z0,z1,z2} U zmin={z0,z1,z2}, найдем точку пересечения линии наибольшего наклона плоскости S к горизонту, проходящую через т. D1, с границами площади АВС, как значение координаты z точки, одновременно удовлетворяющее 2-м условиям: zmin1=min{z6,z7,z8} U zmin1=={zmах, zmin}.
Для решения данной задачи была создана программа в программном продукте Microsoft Excel [4], которая может быть разделена на 2 части: пояснительную и расчетную и приведена ниже.
Пояснительная часть (все части текста в пояснительной и расчетной частях вводятся в программу без кавычек).
Для задания координат точек А, В, С в ячейку В2 необходимо в текстовом формате написать: «Координаты точки А», в ячейку В4 — «Координаты точки В», в ячейку В6 — «Координаты точки С», в ячейку В3 — «х0=», в ячейку В5 — «х1=», в ячейку В7 — «х2=», в ячейку D3 — «y0=», в ячейку D5 — «y1=», в ячейку D7 — «y2=», в ячейку F3 — «z0=», в ячейку F5 — «z1=», в ячейку F7 — «z2=».
Для осуществления наглядности предварительных расчетов необходимо в ячейку С9 в текстовом формате вписать: «Е=», в ячейку С10 — «F=», в ячейку С11 — «H=», в ячейку С12 — «K=», в ячейку С13 — «M=», в ячейку С14 — «N=», в ячейку С15 — «HN=», в ячейку С16 — «EK=», в ячейку С17 — «MF=», в ячейку С18 — «HF=», в ячейку С19 — «EN=», в ячейку С20 — «MK=», в ячейку С21 — «L=», в ячейку С22 — «Q=», в ячейку С23 — «U=», в ячейку С24 — «W=».
Для наглядности представления уравнения S плоскости АВС необходимо в ячейку В25 в текстовом формате вписать: «Уравнение плоскости АВС (плоскости S)», в ячейку B26 — «S=», в ячейку D26 — «* x +», в ячейку F26 — «* y +», в ячейку Н26 — «* z +», в ячейку J26 — «= 0».
C целью подтверждения правильности найденного уравнения S плоскости ABC необходимо в ячейку B30 в текстовом формате вписать: «S(А)=», в ячейку В32 — «S(B)=», в ячейку В34 — «S(C)=».
Для определения принадлежности (или не принадлежности) точки D(x3, y3, z3) плоскости АВС вводим координаты точки D, для чего необходимо в ячейку В37 в текстовом формате вписать: «Координаты точки D (x3={хmах, хmin }, y3={ymах, ymin }) — зададим произвольно», в ячейку В38 — «хmах=max{x0,x1,x2}=», в ячейку В39 — «хmin=min{x0,x1,x2}=», в ячейку D38 — «ymах=max{y0,y1,y2}=», в ячейку D39 — «ymin=min{y0,y1,y2}=», в ячейку B41 в текстовом формате вписать: «х3=», в ячейку D41 — «y3=», в ячейку F41 — «z3=», в ячейку В42 — «S(D)=».
Для определения координаты z4, при которой точка D1c координатами (x4, y4)в плане равными координатам (x3, y3) точки D, будет принадлежать плоскости АВС необходимо в пояснительной части программы в ячейку B45 в текстовом формате вписать: «x4=х3=», в ячейку D45 — «y4=y3=», в ячейку B47– «z4=».
Для проверки правильности определения координаты z4 необходимо в текстовом формате вписать в ячейку В49 — «S(D1) =».
C целью определения расстояния по вертикали от точки D до плоскости АВС необходимо в текстовом формате вписать в ячейку В51 — «R=z3-z4=».
Для определения уравнения горизонтальной прямой D1D2, принадлежащей плоскости S, необходимо в пояснительной части программы в ячейку В52 в текстовом формате вписать: «Определение уравнения горизонтальной прямой D1D2, принадлежащей плоскости S», в ячейку В53 — «Определение координат точки D2», в ячейку В54 — «x5=(xmax-xmin)/2=», в ячейку D54 — «y5=(W-L*x5-U*z5)/Q=», в ячейку F54 — «z5=z4=», в ячейку B55 — «S(D2) =».
![]() С целью определения направляющего вектора прямой D1D2 в ячейку В57 в текстовом формате вписать: «l=x5-x4=», в ячейку В58 — «m=y5-y4=», в ячейку В59 — «n=z5-z4=». Так как нормальный вектор n плоскости Р, перпендикулярной прямой D1D2 и проходящей через точку D1 (x4, y4, z4), совпадает с направляющим вектором прямой D1D2, необходимо в пояснительной части программы в ячейку В61 в текстовом формате вписать: «А1=l=», в ячейку В62 — «В1=m=», в ячейку В63 — «C1=n=», в ячейку В64 — «W1=(A1*x4+B1*y4+C1*z4) =». Далее в ячейку В65 вписываем: «Уравнение плоскости Р:», в ячейку С66 — «* x +», в ячейку Е66 — «* y +», в ячейку G66 — «* z +», в ячейку I66 — «= 0».
С целью определения направляющего вектора прямой D1D2 в ячейку В57 в текстовом формате вписать: «l=x5-x4=», в ячейку В58 — «m=y5-y4=», в ячейку В59 — «n=z5-z4=». Так как нормальный вектор n плоскости Р, перпендикулярной прямой D1D2 и проходящей через точку D1 (x4, y4, z4), совпадает с направляющим вектором прямой D1D2, необходимо в пояснительной части программы в ячейку В61 в текстовом формате вписать: «А1=l=», в ячейку В62 — «В1=m=», в ячейку В63 — «C1=n=», в ячейку В64 — «W1=(A1*x4+B1*y4+C1*z4) =». Далее в ячейку В65 вписываем: «Уравнение плоскости Р:», в ячейку С66 — «* x +», в ячейку Е66 — «* y +», в ячейку G66 — «* z +», в ячейку I66 — «= 0».
С целью определения точек пересечения линии наибольшего наклона плоскости S к горизонту, проходящую через т. D1, с периметром площади АВС, определим точки пересечения плоскости Р с прямыми АВ, ВС, АС, для чего необходимо в ячейку В67 в текстовом формате вписать: «Определение точки пересечения плоскости Р с прямой АВ», в ячейку В68 — «l1=x1-x0=», в ячейку В69 — «m1=y1-y0=», в ячейку В70 — «n1=z1-z0=», в ячейку В71 — «t1=», в ячейку B73 — «х6=х0+l1*t1=», в ячейку D73 — «y6=y0+m1*t1=», в ячейку F73 — «z6=z0+n1*t1=». Далее в ячейку В74 в текстовом формате вписываем: «Определение точки пересечения плоскости Р с прямой ВС», в ячейку В75 — «l2=x2-x1=», в ячейку В76 — «m2=y2-y1=», в ячейку В77 — «n2=z2-z1=», в ячейку В78 — «t2=», в ячейку B80 — «х7=х1+l2*t2=», в ячейку D80 — «y7=y1+m2*t2=», в ячейку F80 — «z7=z1+n2*t2=» и затем в ячейку В81 в текстовом формате вписываем: «Определение точки пересечения плоскости Р с прямой АС», в ячейку В82 — «l3=x2-x0=», в ячейку В83 — «m3=y2-y0=», в ячейку В84 — «n3=z2-z0=», в ячейку В85 — «t3=», в ячейку B87 — «х8=х0+l3*t3=», в ячейку D87 — «y8=y0+m3*t3=», в ячейку F87 — «z8=z0+n3*t3=».
В расчетной части программы в ячейки С3, E3, G3 в численном формате вводим соответственно координаты точки А: x0, y0, z0, в ячейки С5, E5, G5 вводим соответственно координаты точки В: x1, y1, z1, в ячейки С7, E7, G7 вводим соответственно координаты точки С: x2, y2, z2 (точки А, В, С не должны лежать на одной прямой и в одной горизонтальной плоскости).
В части предварительных расчетов программы в ячейку Е9 вводим «=(С5-С3)» (здесь и далее без кавычек), в ячейку Е10 вводим «=(С7-С3)», в ячейку Е11 — «=(Е5-Е3)», в ячейку Е12 — «=(Е16-Е8)», в ячейку Е13– «=(G5-G3)», в ячейку Е14 — «=(G7-G3)», в ячейку Е15 — «=(Е11*Е14)», в ячейку Е16 — «=(Е9*Е12)», в ячейку Е17 — «=(Е13*Е10)», в ячейку Е18 — «=(Е11*Е10)», в ячейку Е19 — «=(Е9*Е14)», в ячейку Е20 — «=(Е13*Е12)», в ячейку Е21 — «=(Е15-Е20)», в ячейку Е22 — «=(Е17-Е19)», в ячейку Е23 — «=(Е16-Е18)», в ячейку Е24 — «=Е21*C3+Е22*E3+Е23*G3».
Для наглядности представления уравнения S плоскости АВС необходимо в ячейку С26 ввести вписать: «=E21», в ячейку Е26 — «=E22», в ячейку G26 — «=E23», в ячейку I26 — «=E24».
Для проверки правильности найденного уравнения S плоскости ABC необходимо в ячейку С30 ввести: «=С26*С3+Е26*Е3+G26*G3-I26», в ячейку C32 — «=С26*С5 +Е26* Е5+G26*G5-I26», в ячейку C34 — «=С26*С7 +Е26* Е7+G26*G7-I26». При этом в ячейках С30, С32, С34 в должен получиться нулевой результат, в противном случае формулы в программе введены неправильно и их необходимо перепроверить.
Для определения максимальных и минимальных значений координат х, y плоскости ABC необходимо в ячейку С38 ввести функцию (через выпадающее меню «Формулы» и вкладку «Вставить функцию»): «=МАКС(С3;С5;С7)», в ячейку C39 — «=МИН(С3;С5;С7)», в ячейку Е38 — «=МАКС(Е3;Е5;Е7)», в ячейку Е39 — «=МИН(Е3;Е5;Е7)». Далее для задания произвольных координат x3, y3 точки D вводим в ячейку C41 любое число из диапазона (xmax-xmin), а в ячейку Е41 любое число из диапазона (уmax-уmin), в ячейку G41 вводим вообще любое число для задания координаты z3.
Для определения принадлежности (или не принадлежности) точки D(x3, y3, z3) плоскости АВС вводим координаты точки D в уравнение плоскости S, для чего в ячейку С42 вводим формулу: «=C26*C41+E26*E41+G26*G41-I26». Так как координата z3 принята произвольно, то, скорее всего, точка D не будет принадлежать плоскости АВС и в ячейке С42 будет ненулевой результат. Если получиться нулевой результат, то изменить число в ячейке G41. В случае повторения нулевого результата необходимо перепроверить формулы в программе, т. к. они введены неправильно.
Для определения координаты z4, при которой точка D1c координатами (x4= x3, y4= y3)в плане будет принадлежать плоскости S необходимо в расчетной части программы в ячейку С45 ввести формулу: «=C41», в ячейку Е45 — «=E41», в ячейку Е47– «=(E24-E21*C45-E22*E45)/E23».
Для определения проверки принадлежности (или не принадлежности) точки D1(x4, y4, z4) плоскости АВС вводим координаты точки D1 в уравнение плоскости S, для чего в ячейку С49 вводим формулу: «=C26*C45+E26*E45+G26*E47-I26», при этом должен получиться нулевой результат (в противном случае перепроверить формулы в программе).
C целью определения расстояния по вертикали от точки D до плоскости АВС необходимо ввести в ячейку С51 — «=G41-E47».
Для определения уравнения горизонтальной прямой D1D2, принадлежащей плоскости S, необходимо в расчетной части программы в ячейку С54 ввести формулу: «=(C38-C39)/2», в ячейку Е54 — «=(E24-E21*C54-E23*G54)/E22», в ячейку G54 — «=E47».
Для определения проверки принадлежности (или не принадлежности) точки D2(x5, y5, z5) плоскости АВС вводим координаты точки D2 в уравнение плоскости S, для чего в ячейку С55 вводим формулу: «=C26*C54+E26*E54+G26*G54-I26», при этом должен получиться нулевой результат (в противном случае перепроверить формулы в программе).
С целью определения направляющего вектора прямой D1D2 в ячейку С57 ввести формулу: «=C54-C45», в ячейку С58 — «=E54-E45», в ячейку С59 — «=G54-E47».
![]() С целью определения нормального вектора n плоскости Р в ячейку С61 ввести формулу: «=C57», в ячейку С62 — «=С58», в ячейку С63 — «=С59», в ячейку С64 — «=(C61*C45+C62*E45+C63*E47)».
С целью определения нормального вектора n плоскости Р в ячейку С61 ввести формулу: «=C57», в ячейку С62 — «=С58», в ячейку С63 — «=С59», в ячейку С64 — «=(C61*C45+C62*E45+C63*E47)».
Для наглядности представления уравнения плоскости Р в ячейку В66 вводим формулу: «=C61», в ячейку D66 — «=C62», в ячейку F66 — «=C63», в ячейку Н66 — «=C64».
Для определения точки пересечения плоскости Р с прямой АВ необходимо в ячейку С68 ввести формулу: «=C5-C3», в ячейку С69 — «=E5-E3», в ячейку С70 — «=G5-G3», в ячейку С71 — «=-(C61*C3+C62*E3+C63*G3-C64)/(C61*C68+C62*C69+C63*C70)», в ячейку С73 — «=C3+C68*C71», в ячейку Е73 — «=E3+C69*C71», в ячейку G73 — «=G3+C70*C71». Для определения точки пересечения плоскости Р с прямой ВС необходимо в ячейку С75 ввести формулу: «=C7-C5», в ячейку С76 — «=E7-E5», в ячейку С77 — «=G7-G5», в ячейку С78 — «=-(C61*C5+C62*E5+C63*G5-C64)/(C61*C75+C62*C76+C63*C77)», в ячейку С80 — «=C5+C75*C78», в ячейку Е80 — «=E5+C76*C78», в ячейку G80 — «=G5+C77*C78». Для определения точки пересечения плоскости Р с прямой АС необходимо в ячейку С82 ввести формулу: «=C7-C3», в ячейку С83 — «=E7-E3», в ячейку С84 — «=G7-G3», в ячейку С85– «=-(C61*C3+C62*E3+C63*G3-C64)/(C61*C82+C62*C83+C63*C84)», в ячейку С87 — «=C3+C82*C85», в ячейку Е87 — «=E3+C83*C85», в ячейку G87 — «=G3+C84*C85».
В результате реализации программы, задавая координаты x3, y3 в плане любой точки D внутри любой площади АВС (это могут быть координаты опор различного оборудования, арматуры, фитингов и др.) возможно найти вертикальную координату проекции точки D (точки D1) на плоскость АВС, определить расстояние R от точки D до плоскости (это может быть высота строительной конструкции и т. п.), определить горизонтальную линию и линию максимального наклона плоскости к горизонту, принадлежащие плоскости АВС и проходящие через точку D1, а также координаты точек пересечения последней линии с границами плоскости — прямыми АВ, ВС, АС. Изменяя координаты z0, z1, z2 точек А, В, С соответственно, имеется возможность подбора необходимых при проектировании нормативных значений направления и уклона линии максимального наклона плоскости к горизонту (например к сбросному клапану проектируемой площадки и т. п.). Кроме того, определение в программе уравнений плоскостей S и Р, а также всех линий, дает возможность определить и любые другие геометрические параметры проектируемой площади и манипуляции с ней.
Литература:
- СНиП 11–02–96. Инженерные изыскания для строительства. Основные положения. (Утвержден приказом Госстроя РФ от 10.12.2012 г. № 83/ГС).
- СП 11–104–97. Инженерно-геодезические изыскания для строительства» (одобрен Письмом Госстроя РФ от 14.10.1997 № 9–4/116).
- Шипачев В. С. Высшая математика: Учеб. для немат. спец. вузов / Под ред. акад. А. Н. Тихонова. — 2-е изд., стер. М.: Высш. шк., 1990. — 479 с., ил.
- Инструкция по использованию программного обеспечения Microsoft Excel программного продукта «Microsoft Office профессиональный плюс 2010» корпорации Майкрософт (Microsoft Corporation).







