Автоматизация проектирования маршрутов обхода геометрических объектов на плоскости

Рассматривается модифицированный метод колонии муравьев для решения задачи построения кратчайшего гамильтонова цикла на множестве отрезков и ломаных на плоскости. Показана эффективность разработанного метода, приведен сравнительный анализ решений, полученных с помощью различных эвристик.

Ключевые слова: гамильтонов цикл, колония муравьев.

1. Введение

На практике часто возникают ситуации, когда необходимо построить кратчайший маршрут проезда между заданными точками или наилучшим образом разместить пункты сервиса на дорогах, предприятия на территории, коммутаторы в телефонной сети и т.п. Это широко известные задачи маршрутизации и размещения. Многие из таких задач могут быть описаны с помощью оптимизационных моделей и сведены к решению дискретных задач.

Решение NP-полных задач дискретной оптимизации с произвольной размерностью исходных данных вызывает сложность даже при использовании вычислительных средств большой мощности. В настоящее время не существует методов получения точного решения за время, ограниченное условиями функционирования информационной системы или продолжительностью технологических операций. Поэтому суть современных методов решения таких задач заключается в выборе лучшего варианта при проверке некоторого подмножества всех возможных альтернатив. При этом подразумевается, что ошибка найденного решения не слишком велика и решение будет близко к оптимальному. К сожалению, в большинстве случаев величина ошибки приближенного решения не может быть определена.

Методы, основанные на управлении поиском в пространстве решений, к числу которых относится рассматриваемый ниже метод колонии муравьев, используют в разной мере математическую конструкцию цепей Маркова [1]. Поиск эвристик ограничения пространства возможных решений, как правило, не формализован. С помощью современных средств вычислительной техники можно исследовать NP-полные задачи на данных сравнительно малой размерности, выявлять закономерности распределения оптимальных решений в пространстве поиска решений. Найденные эвристики можно рекомендовать для решения задач произвольной размерности, предварительно доказав их эффективность и статистическую устойчивость. Однако обоснованность переноса закономерностей, установленных в ходе исследований, на задачи с большой размерностью исходных данных остается под вопросом.

Рассмотрим задачу оптимизации движения режущего инструмента в станках с ЧПУ [2, 3]. В процессе программирования работы станка термической резки металла или графопостроителя возникает задача минимизации длины маршрута пера (режущего инструмента), в частности, в тех случаях, когда перо перемещается в режиме холостого хода между точками врезки или точками начала отрисовки контура. При анализе карт раскроя также возникает необходимость локальной оптимизации, вызванная технологическими ограничениями или вмешательством оператора.

Описанная задача маршрутизации близка к классической задачи поиска маршрутов обхода на множестве точек (пунктов), рассматриваемой в теории графов. Чтобы провести аналогию, заменим точки отрезками и построим на отрезках кратчайший замкнутый цикл – гамильтонов цикл. Поскольку очевидна общность задач поиска маршрутов на множестве точек и множестве кусочно-ломаных траекторий, целесообразно представить исходное множество в терминах теории графов.

Большинство исследований в решении подобных задач направлены на построение маршрутов обхода отрезков на основе графа видимости концов отрезков (segment endpoint visibility graph) либо на выделении отдельных подмножеств отрезков (например, множества независимых и цело-координатных отрезков) и разработке для них итерационных процедур [4– 12]. Такая постановка задачи значительно сужает область применения разработанных методов.

Решаемая задача заключается в автоматизации проектирования оптимальных траекторий замкнутых маршрутов в двумерной дискретной области, заданной произвольным множеством непересекающихся отрезков или элементами технологической карты раскроя.

2. Постановка задачи

На произвольном множестве неориентированных непересекающихся отрезков (рис. 1а) необходимо построить минимальный по длине маршрут обхода всех отрезков (кратчайший гамильтонов цикл, рис. 1б).

                                            

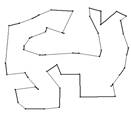
а)                                                 б)

Рис. 1. Гамильтонов цикл на произвольном множестве отрезков

Если вершины графа – точки концов отрезков (ломаные и замкнутые контуры также представлены в виде набора отрезков, имеющих общие концы), то ребра – всевозможные переходы между концами отрезков, включающие, конечно, и сами отрезки. Полученный граф – полносвязный, неориентированный, взвешенный. В качестве весов ребер выступают расстояния между концами отрезков.

В маршрут обхода включаются все отрезки (ломаные), пройденные однократно, и переходы между отрезками (суммарную длину которых и необходимо минимизировать). Маршрут замкнутый, то есть заканчивается в исходной точке.

Если руководствоваться только расстоянием между отрезками, то метод решения задачи можно искать среди различных метаэвристик (сложность точных методов находится в экспоненциальной зависимости от размерности задачи). Однако при рассмотрении весов ребер графа вполне закономерно предположение о введении дополнительных оценок весов и построении решения на основе уже двух (а возможно и более) величин. Остановимся на двух весах: константном (расстоянии) и переменном (основанном на механизме запоминания лучшего решения).

Поскольку обход отрезка может начинаться с любого конца, а обход замкнутого контура – с любого его звена, логично предположить, что алгоритм поиска общего маршрута также должен иметь возможность начать строить решение с любого конца отрезка или части контура. Такое свойство можно соотнести с синхронностью (мультистартовостью) поиска. Если построение решения начинается со всех точек, то и выбор последующей осуществляется среди всего множества допустимых (поливекторность поиска).

Описанные характеристики согласуются со свойствами многоагентных методов, в частности, метода муравьиной оптимизации.

2. Метод колонии муравьев

Идею метода, не используя бионические термины, можно представить следующим образом. На первом шаге производится произвольное построение маршрута из множества допустимых (отслеживается условие построения простого замкнутого цикла). Выбор осуществляется по принципу ближайшего соседа либо случайным образом. Решение ищется, начиная со всех отрезков одновременно. Из полученных n решений (n – число отрезков исходного множества) выбирается лучшее (оценка целевой функции производится как по длине результирующего маршрута, так и по количеству самопересечений маршрута). Ребра, входящие в лучшее решение, получают дополнительные веса. На последующих итерациях учитываются уже новые веса. Таким образом, лучшие маршруты становятся все более привлекательными. Причем изменение переменной составляющей весов ребер проходит в два этапа: локальное обновление и глобальное. При глобальном изменении увеличиваются веса ребер, входящих в лучший маршрут на данной итерации. При локальном изменении – увеличиваются веса ребер, включенных в маршрут каждого решения. Во втором случае происходит изменение окрестности локального поиска.

Чтобы избежать «зацикливания» процесса, то есть ситуации, когда быстрое увеличение переменной составляющей веса, приводит к снижению вероятности поиска новых решений, используется обратная процедура – уменьшение веса ребра. Вышеописанный процесс изменения переменного веса ребер в зависимости от получаемого решения, в соответствии с характером алгоритма, можно назвать механизмом обратной связи (положительной). На первых этапах решения большее значение имеет постоянный вес ребра, на последующих – переменный, то есть информация о глобальном минимуме.

Поскольку при выборе последующего пункта маршрута используются два веса, возникает задача их соотношения. Если превалирует постоянный вес ребра, то решение принимается на основе принципа жадности, то есть в маршрут включается ближайший из допустимых отрезков. При доминировании переменного параметра, выбирается отрезок, который уже был «опробован» на предыдущих этапах. И первый, и второй вариант, в чистом виде, не гарантируют эффективную работу алгоритма. В «жадных» алгоритмах решение находится быстро, однако может быть сколь угодно далеко от оптимального. В алгоритмах, основанных на механизме закрепления лучшего среди найденных решения, возникает ситуация стагнации.

В случаях, когда исходное множество содержит ломаные или замкнутые контуры, возникает вопрос о непрерывности их обхода (сквозном проходе). При полном запрете прерывания обхода необходимо учитывать типы возникающих пересечений маршрута (самопересечение или пересечение контура) и технологические ограничения (холостой ход резца или активный режим). В общем случае процесс обхода контуров можно сделать управляемым. С помощью дополнительного параметра веса ребер, представляющих отрезки, можно установить соотношение между возможностью и запретом прерывания обхода контура. В этом случае нет необходимости фиксировать точку входа в контур, а также изменять режим работы резца инструмента. Такое представление удобно при работе в интерактивном режиме.

Используя бионические термины и термины методов семейства муравьиной оптимизации [13 – 15], математическую модель эвристического метода Ant Colony Routing, метаэвристики колонии муравьев, можно представить следующим образом.

Элементами эвристики колонии муравьев являются:

- простые агенты, наделенные определенными свойствами;

- некоторая информация о локальном положении (численная характеристика перехода между звеньями маршрута, призванная охарактеризовать полезность звена для построения конечного решения);

- механизм принятия решения – выбора последующего звена.

Простые агенты – муравьи – наделены памятью, а также способностью оценивать локальную информацию. Существуют они, очевидно, в дискретном времени.

Информация о местоположении муравья и характеристиках соседних объектов представлена двумя параметрами: феромоном и расстоянием. Оба параметра описывают переход между парой точек: текущей, в которой находится муравей, и одной из множества допустимых. Расстояние – константа, отражающая физическую близость между двумя точками. Видимость пути 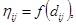– величина, обратная расстоянию между начальной и конечной точкой отрезка пути i и j соответственно. Феромон –  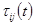- величина переменная, описывающая привлекательность пути с точки зрения уже имеющихся решений, полученных на предшествующих шагах итерации или на предыдущих итерациях. Понятие феромона создатели метода заимствовали у природных муравьев-аналогов. Феромон – пахучее вещество, оставляемое каждым муравьем на пути следования. Чем больше феромона на пути, тем больше муравьев выберут этот путь (эффект обратной связи). При моделировании феромона в нашей системе используется коэффициент– положительное число, для вычисления величины которой (и, следовательно, привлекательности данного отрезка пути) рассматривается длина наименьшего пути, найденного со времени начала поиска, а также коэффициенты обновления (испарения и добавления) феромона, что позволяет управлять выбором пути.

Так, обновление феромона после определения лучшего решения на данной итерации, задается формулой

,

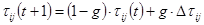где 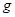 - коэффициент глобального испарения, 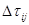- добавление феромона, которое рассчитывается как:

,

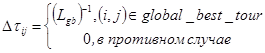где 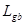 - длина наименьшего пути (global_best_tour), найденного со времени начала поиска.

На каждой итерации алгоритма осуществляется ряд процедур:

- построение начального решения,

- выбор из множества возможных переходов подмножества допустимых,

- процедура оценки перехода из подмножества допустимых,

- добавление звена в частичное решение,

- изменение характеристик звеньев, входящих в частичное или полное решение (обновление феромона),

- преобразование последовательности переходов в решение задачи поиска маршрута.

Возможно также добавление методов локального улучшения решения.

В общем случае вероятность перехода из точки i в точку j на t-ой итерации определяется:

,

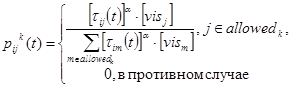где 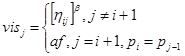 и ,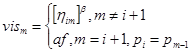

при этом 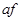 – adjacent force – коэффициент смежности,  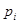– конец отрезка i,  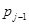– конец отрезка j; 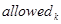- список отрезков, ещё не пройденных k-ым муравьём, 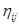– видимость пути, 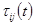- величина феромона на аугментальной дуге (i, j), α и β - параметры, контролирующие относительный приоритет феромона на пути и видимости следующего отрезка (важность феромона и коэффициент видимости пути соответственно).

Вероятность включения ребра в маршрут отдельного муравья пропорциональна количеству феромонов на этом ребре, а количество откладываемого феромона пропорционально длине маршрута. Чем короче маршрут, тем больше феромона будет отложено на его ребрах, следовательно, большее количество муравьев будет включать его в синтез собственных маршрутов.

Моделирование подхода, использующего только положительную обратную связь, приводит к преждевременной сходимости – большинство муравьев двигается по локально-оптимальному маршруту. Избежать этого можно, моделируя отрицательно обратную связь в виде испарения феромона. Причем, если феромон испаряется быстро, то это приводит к потере памяти колонии и «забыванию» хороших решений, с другой стороны, большое время испарений может привести к получению устойчивого локального оптимального решения.

Если муравей находится на ломаной, то вместо коэффициента видимости пути используется коэффициент смежности. При увеличении значения коэффициента смежности муравей пытается выстроить путь, не покидая текущий контур. Строго говоря, необходимо заставить муравья пройти весь контур (ломаную) целиком без рассмотрения возможности перехода на другие отрезки. Это значительно ограничит область допустимых решений. Однако в общем случае возможно прерывание обхода контура, поскольку мы не оговаривали ограничение на сквозной проход. Значение коэффициента смежности отрезков выбирается таким образом, чтобы нейтрализовать действие механизма обратной связи, то есть, чтобы величина коэффициента была сравнима или превосходила величину феромона на дугах.

В рассмотренном алгоритме функциональной зависимости между параметрами не найдено, однако подобраны значения, обеспечивающие оптимальную работу алгоритма.

3. Исследование свойств метода колонии муравьев

Рассмотрим статистическую устойчивость разрабатываемого метода (рис. 2). При многократном запуске программы 57% решений отличаются не более чем на 5% от минимального. Около 30% решений попадают в 10-процентную окрестность минимального решения и нет решений, отличающихся от минимального более чем на 30%.

Еще одним фактором, характеризующим эффективность алгоритма, является его устойчивость. Поскольку алгоритм носит вероятностный характер, необходимо исследовать его поведение при многократном решении одной и той же задачи. На рис.3 показана величина лучшего решения, найденного на соответствующем по номеру запуске программы. Отклонение от средней длины маршрута составляет порядка 5%.

 

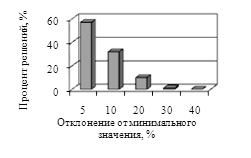
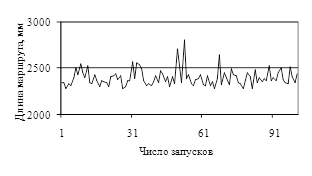
Рис.2. Отклонение от минимальной длины маршрута

Рис.3. Изменение длины маршрута при увеличении числа запусков программы

Сходимость метода колонии муравьев можно рассматривать как переход итерационного процесса в устойчивое состояние и получение эффективного решения за определенное количество итераций. Это свойство вытекает из его способности постоянно улучшать качество решения (рис.3).

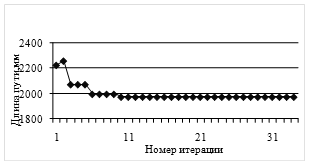
Рис.3. Изменение длины маршрута в зависимости от количества итераций алгоритма

Для подтверждения эффективности описанного метода решим задачу с помощью популярной эвристики – метода ближайшего соседа, адаптированного случайного поиска и с помощью метода обратной связи (без учета параметра видимости пути), см. табл.1.

В качестве сравниваемых параметров рассмотрим длину найденного решения L (mm), число итераций, за которое найдено лучшее решение (n), среднее межотрезковое расстояниеl (mm), время работы алгоритма t (ms), число пересечений пути в найденном решении Nint.

Таблица 1

Сравнительный анализ решений

При решении задачи без учета видимости пути наблюдалось ухудшение результата (данные в скобках четвертого столбца). Это объясняется неустойчивостью такой модификации алгоритма к начальным условиям, случайным характером поиска и низкой скоростью поиска глобального минимума.

Как следует из таблицы, метод ближайшего соседа находит не лучшее решение, однако за малое число итераций, что подтверждает общие характеристики принципа жадности: поиск локального минимума за малое время. Учет одного лишь феромона (использование механизма обратной связи) не способствует быстрому решению задачи.

Временная сложность алгоритма определяется, в частности, самыми трудоемкими этапами (построение матрицы решения - выбор последующего отрезка и вычисление длины маршрута каждого муравья, изменение весов ребер графа входящих в лучший маршрут). При условии, что число отрезков равно числу муравьев (n = m) сложность итерации алгоритма составляет .

4. Заключение

Предлагаемый алгоритм позволяет эффективно решать задачи построения маршрутов обхода геометрических объектов, заданных множеством отрезков. В среднем, метод колонии муравьев дает решения, лучшие на 20% (по критерию длины итогового пути) по сравнению с простейшими эвристиками, основанными на принципе жадности. Случайный поиск привел к неудовлетворительному решению с очень большим числом самопересечений пути. Вычислительная сложность итерации алгоритма составляет .

Применение разработанных алгоритмов в процессе автоматизации проектирования управляющих программ станков с ЧПУ позволяет не только повысить коэффициент использования оборудования (по оценкам, на 3 – 5%), но и снизить энергетические затраты на резку металла, увеличить ресурс использования режущего инструмента, сократить сроки проектирования управляющих программ, повысить качество проектных решений.

 

ЛИТЕРАТУРА

 

[1]Кочетов Ю.А. Вероятностные методы локального поиска для задач дискретной оптимизации // Дискретная математика и ее приложения: Сборник лекций молодежных и научных школ по дискретной математике и ее приложениям.- М.: Издательство центра прикладных исследований при механико-математическом факультете МГУ. - 2000. – С. 87-117.

[2]Фроловский В.Д., Эстрайх И.В. Об одной задаче оптимизации движения режущего инструмента при раскрое листового проката // Машинные методы оптимизации, моделирования и планирования эксперимента. – Новосибирск: НЭТИ, 1988. – С. 60-65.

[3]Frolovsky V.D., Pushkaryova G.V. Metal cutting motion optimization for NC-programs design, using genetic algorithms // Proc. of the 6th International Conference in Computer Graphics and Artificial Intelligence (3IA’2003). – May, 2003, Limoges (France). – P. 143-152.

[4]       Leipala T., Nevalainen O. A plotter sequencing system // The Computer Journal. - 1979; 22:313-316.

[5]       Mirzaian A. Hamiltonian triangulations and circumscribing polygons of disjoint line segments // Computational Geometry Theory and Applications. – 1992. - 1:15–30.

[6]       Garey M.R., Johnson D.S., Tarjan R.E. The planar Hamiltonian circuit problem is NP-complete // SIAM J. Comput. - 1976. -5:704-714.

[7]       O'Rourke J., Rippel J. Two Segment Classes with Hamiltonian Visibility Graphs // Computational Geometry: Theory and Applications. – 1994. - 1:209-218.

[8]       Rappaport D. Computing simple circuits from a set of line segments is NP-complete // SIAM Journal on Computing. -1989. - Vol.18. – 6:1128-1139,

[9]       Rappaport D. Minimum polygon transversals of line segments // Computational Geometry: Theory and Applications. -1995. - 5:243-256.

[10]    Rappaport D. The visibility graph of congruent discs is Hamiltonian // Computational Geometry: Theory and Applications. – 2003.- 25:257-265.

[11]    Rappaport D, Imai H., Toussaint G. Computing simple circuits from a set of line segments // Discrete Computational Geometry. -1990. - 5(3):289-304.

[12]    Grunbaum B. Hamiltonian polygons and polyhedra. // Geombinatorics. – 1994.-3:83 - 89.

[13]    Dorigo M., Maniezzo V., Colorni A. The Ant System: Optimization by a colony of cooperating agents. // IEEE Transactions on Systems, Man and Cybernetics. – 1996. - Part B, Vol. 26.- 1:1 – 13.

[14]    Dorigo M., Caro G., Gambardella L. Ant Algorithms for Discrete Optimization // Artificial Life. - 1999. - 5(2):137-172.

[15]    Gutjahr W. A generalized convergence result for the graph-based ant system metaheuristic // Probability in the Engineering and Informational Sciences. -2003. -P.545 – 569.