Управление транспортными комплексами, в целом, и отдельными производственными процессами, в частности, осуществляется на транспорте, как правило, в условиях высокой степени неопределенности. Второй важной особенностью деятельности транспортных систем является нестационарность функционирования, как среды, так и собственно объекта исследования. Это актуализирует необходимость создания адаптивных схем и методов управления, обладающих свойствами интеллектуального функционирования.
Развитие интеллектуальных технологий – основа обеспечения живучести и безопасности систем железнодорожного транспорта /1/. В этой связи научно-технический прогресс отрасли связывается ее высшим менеджментом с созданием интеллектуального железнодорожного транспорта. Работы в этом направлении уже активно ведутся, в частности, на сети внедряется разработка интеллектуального поезда (как пассажирского, так и грузового).
В данной работе предлагается механизм статистического анализа неопределенной ситуации и формирование на его базе советующего устройства, позволяющего снизить влияние неопределенности и учесть нестационарность процесса. Этим повышается качество управления. Суть разрабатываемого механизма в расчете и сравнении рисков возникновения различных ситуаций.
Предполагается, что система управления объектом обладает подсистемами: мониторинга, базой данных (БД) и базой знаний (БЗ). Первая обеспечивает сбор необходимой информации, вторая – структурирует и хранит ее, третья обеспечивает интеллектуальный анализ данных. Такой подход позволяет учесть опыт работы конкретного объекта в конкретных условиях.
Для придания изложению большей четкости и наглядности проиллюстрируем все предлагаемые выкладки конкретным примером, решение которого имеет самостоятельное теоретическое и практическое значение. Технологическая задача состоит в следующем. Необходимо обеспечить в процессе роспуска составов на горке, не допуская «окон» и боя вагонов и грузов, прицельное регулирование скатывающимися с сортировочной горки отцепами (рис. 1).
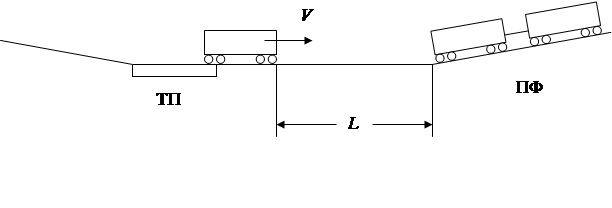
Рис. 1. – Профиль участка сортировочной горки
Факторы, создающие неопределенность ситуации и нестационарность процесса управления скатыванием отцепов: тип бегуна, параметры среды. Действительно, характеристики отцепа, влияющие на режим скатывания: вес, тип подшипника, род вагонов, число вагонов и осей и т.д. не определяют достоверно ходовые свойства отцепа. Тип бегуна изменяется и с течением времени в зависимости от температуры, влияющей на скольжение, направления и силы ветра. Режим скатывания зависит также от состояния путевой структуры горки.
Введем понятие управляемой ситуации, характеризуемой двойкой:
Si = (Ti, Li). (1)
В соотношении (1) T означает тип бегуна, например, Х – хороший, С – средний, П – плохой. Переменная L определяет расстояние до точки прицеливания. Индекс i – номер исследуемой ситуации.
Предполагается, что число возможных ситуаций ограничено. Это не жесткое ограничение для исследуемого процесса, не снижающее общности, но значительно упрощающее процедуру расчета. Действительно, масса и подшипник отцепа, определяющие его ходовые свойства принимают дискретные значения на ограниченных промежутках, измерение длины пути аналогично предыдущему дискретно (по числу свободных участков рельсовой цепи).
Управляющим воздействием является скорость выхода отцепа Vj из тормозной позиции (ТП). Эта величина также может рассматриваться как дискретная в силу того, что существуют ошибки как при вытормаживании отцепов на ТП, так и при измерении скорости. В пределах диапазона ошибки скорость можно считать постоянной (неразличимой).
Введенные предположения позволяют построить таблицу соответствий, складывающихся на ТП ситуаций и возможных управлений (табл. 1).
Таблица 1. – Статистика управления отцепами на ТП
|
Vj Si |
V1 |
V2 |
…
|
Vm
|
|
S1 |
(n111, n211, n311) |
(n112, n212, n312) |
… |
(n11m, n21m, n31m) |
|
S2 |
(n121, n221, n321) |
(n122, n222, n322) |
… |
(n12m, n22m, n32m) |
|
… |
… |
… |
… |
… |
|
Sn |
(n1n1, n2n1, n3n1) |
(n1n2, n2n2, n3n2) |
… |
(n1nm, n2nm, n3nm) |
Таблица заполняется по результатам статистических наблюдений за исследуемым процессом. В поле таблицы компоненты вектора (n1ij, n2ij, n3ij) означают соответственно: число правильно скатившихся отцепов, число образовавшихся «окон», число роспусков отцепов с превышением допустимой скорости соударения. По результатам наблюдений табл. 1 легко рассчитывается таблица соответствующих вероятностей:
(р1ij, р2ij, р3ij). (2)
где
ркij = nкij / (n1ij + n2ij + n3ij).
Эти вероятности означают соответственно долю правильных роспусков отцепов и риски образования «окон» или боя вагонов и грузов в паре (Si , Vj), то есть, если в ситуации Si применили управление Vj. В таблице 2 приведен конкретный пример при n = 3 и m = 4.
Таблица 2. – Вероятности возникновения пар «ситуация - управление» (Si , Vj)
|
Vj Si |
V1 |
V2 |
V3
|
V4
|
|
S1 |
(0,1; 0,3; 0,6) |
(0,2; 0,5; 0,3) |
(0,4; 0,4; 0,2) |
(0,5; 0,3; 0,2) |
|
S2 |
(0,2; 0,4; 0,4) |
(0,3; 0,4; 0,3) |
(0,5; 0,4; 0,1) |
(0,3; 0,5; 0,2) |
|
S3 |
(0,4; 0,4; 0,2) |
(0,5; 0,4; 0,1) |
(0,3; 0,3; 0,4) |
(0,3; 0,4; 0,3) |
Рассматриваемые три ситуации могут соответствовать трем типам отцепов Х, С, П при постоянном расстоянии L. Для различных L формируются в БД соответствующие таблицы. Технология работы с таблицами – предмет содержания БЗ (см. далее формулы (3) – (6)). Исследуем некоторые случаи выбора управления.
Если сложилась ситуация S1, то очевидно, что наилучшим управлением будет V4. При этом с минимальной вероятностью образуются «окна» и бой вагонов и с максимальной вероятностью будет обеспечено надежное сцепление отцепа с составом в парке формирования (ПФ).
Если сложилась ситуация S3 , то по критериям нормального сцепления и минимизации боя следует выбрать решение V2, а по критерию минимизации «окон» необходимо использовать решение V3.
В силу неопределенности характеристик отцепа его принадлежность к выделенным типам Х, С и П , а следовательно и к ситуациям S1, S2, S3 в ряде случаев достоверно определить не удается. Пусть известны вероятности этих ситуаций: q1 , q2 , q3. Требуется обеспечить наилучшее управление отцепом на ТП «в среднем». Для этой цели используются следующие соотношения, трактующие величины (р1ij, р2ij, р3ij) как «цену» принятия того или иного решения.
При удовлетворении требования наилучшего сцепления отцепов в парке формирования (ПФ):
jопт1 = arg maxj ∑1n qi р1ij . (3)
При необходимости минимизации размеров «окон»:
jопт2 = arg minj ∑1n qi р2ij . (4)
При минимизации потерь от боя вагонов и грузов:
jопт3 = arg minj ∑1n qi р3ij . (5)
Соотношения (3) – (5) характеризуют процедуру минимизации среднего риска принятия решения /2/.
Пусть в примере табл. 2 известны вероятности принадлежности отцепа к ситуациям S1, S2, S3, соответственно равны: 0,3; 0,5; 0,2. Результаты расчетов по формулам (3) – (5) дают следующие результаты:
jопт1 = arg max(0,21; 0,31; 0,43; 0,36) = 3,
jопт2 = arg min(0,37; 0,43; 0,38; 0,42) = 1,
jопт3 = arg min(0,46; 0,26; 0,19; 0,22) = 3.
Лучший результат по надежному сцеплению и минимум боя дает вариант jопт = 3, а лучшим с точки зрения минимума «окон» дает вариант jопт =1. Следует отметить, что различие первого и третьего вариантов управления по второму критерию незначительно.
Нестационарность процесса легко учесть, если вероятности (р1ij, р2ij, р3ij) периодически перерассчитываются по последним данным об управлении отцепами. Для каждой тормозной позиции следует рассчитывать свою модель.
Если исследуется процесс, относительно которого отсутствуют статистические данные наблюдений, то возможен переход к экспертному определению значений вектора (р1ij, р2ij, р3ij) , которые будут рассматриваться в качестве функций принадлежности нечетких множеств, и далее к композиции нечетких множеств, обобщающей процедуру принятия решения по минимуму риска.
Рассмотрим еще одну постановку задачи принятия решения, обеспечивающую интеллектуальность функционирования сортировочной горки, и опирающуюся на минимаксную процедуру принятия решений /2/. Для различных скоростей v роспуска отцепов (управлений) и заданным критериям живучести – fж(v), технологической безопасности – fтб(v), экономической безопасности – fэб(v) экспертами задана таблица 3 стоимостей (значений критериев).
Таблица 3. – Значения критериев живучести и безопасности при различных скоростях скатывания отцепов
|
v |
2 |
3 |
3,5 |
4 |
4,5 |
5 |
|
fж(v) |
0,85 |
0,7 |
0,65 |
0,5 |
0,35 |
0 |
|
fтб(v) |
0,9 |
0,8 |
0,75 |
0,7 |
0,6 |
0,55 |
|
fэб(v) |
0,4 |
0,6 |
0,65 |
0,8 |
0,9 |
1 |
|
min |
0,4 |
0,6 |
0,65 |
0,5 |
0.35 |
0 |
Минимаксная процедура, определяемая соотношением:
v = arg maxi minj aij , (6)
дает решение v = 3,5. Смысл ее состоит в нахождении гарантированного результата:
- на первом этапе для каждого управления (в нашем случае скорости роспуска v) находится наиболее критичный показатель;
- на втором выбирается наибольший из них;
- на третьем определяется управление, обеспечивающее это значение.
Литература:
1.Шабельников А.Н. Интеллектуальные системы управления на железнодорожном транспорте. Монография. Ростов-на-Дону, 2004. – 214 с.
2.Лябах Н.Н., Шабельников А.Н. Техническая кибернетика на железнодорожном транспорте: Учебник. – Ростов-на-Дону: Издательство СКНЦ ВШ, 2002. – 283 с.







