В статье приводятся результаты прогнозирования налоговых поступлений в региональный бюджет. Прогнозирование налоговых поступлений осуществляется на основе однородной и разнородной информации по данным управления федеральной налоговой службы по Забайкальскому краю.
Актуальность
Управление налоговыми органами связано с принятием решений в условиях неопределенности и большого объема самой разнородной информации. Специалистам налоговых органов приходится ежедневно сталкиваться с выбором управленческих решений, направленных на повышение результативности работы по налоговым поступлениям в бюджет. Поэтому возникает необходимость в проведении исследований, направленных на повышение эффективности работы налоговых органов. Создание моделей прогнозирования налоговых платежей является актуальным вопросом для управления налоговыми органами.
Построение модели
Основные методы анализа временных рядов заключаются в извлечении из зашумленных данных тенденций развития временного ряда. Однако, прогнозы, основанные исключительно на таких методах, успешны лишь в том случае, если эти тенденции не изменяются во времени. Практически это случается редко, поэтому наиболее важные прогнозы в промышленности, экономике и политике включают экспертные суждения того или иного вида. Эксперту - специалисту в проблемной области естественно судить о нижней и верхней границах возможных значений временного ряда на периоде упреждения прогноза. Эксперт также может судить о том, будут ли монотонно убывать или возрастать значения ряда с течением времени, и если не будут, то в какой момент следует ожидать достижения максимального или минимального значений.
Каждое суждение w может быть представлено в виде сложного высказывания алгебры логики, составленного посредством логических связок 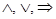 из элементарных высказываний v вида
из элементарных высказываний v вида 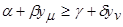 , где моменты периода упреждения μ, ν и величины α, β, γ, δ задаются экспертами. Можно представить экспертное суждение в виде кортежа <α, β, γ, δ, μ, ν>. Например, запись <0, 1, a, 0, t, t+1>
, где моменты периода упреждения μ, ν и величины α, β, γ, δ задаются экспертами. Можно представить экспертное суждение в виде кортежа <α, β, γ, δ, μ, ν>. Например, запись <0, 1, a, 0, t, t+1> 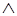 <b, 0, 0, 1, t-1, t> означает «Значение временного ряда в момент t периода упреждения прогноза окажется в интервале [a, b]».
<b, 0, 0, 1, t-1, t> означает «Значение временного ряда в момент t периода упреждения прогноза окажется в интервале [a, b]».
Полагаем, что известны предыстория прогнозируемого явления в виде последовательности результатов наблюдений 
 и множество непротиворечивых экспертных суждений
и множество непротиворечивых экспертных суждений 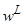 . С точностью до параметров определим модель
. С точностью до параметров определим модель 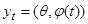 . Задача состоит в отыскании прогнозной модели, наиболее согласованной с результатами наблюдений и экспертными суждениями [2].
. Задача состоит в отыскании прогнозной модели, наиболее согласованной с результатами наблюдений и экспертными суждениями [2].
Поскольку соответствие модели результатам наблюдений определяется тем, насколько вычисленные по модели значения временного ряда близки к наблюдаемым, то в качестве меры близости примем сумму
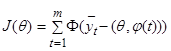 . (1)
. (1)
В результате приходим к задаче минимизации  при ограничениях, которые задаются экспертными суждениями. Решение задачи в произвольном случае предлагается выполнять методом множителей Лагранжа, когда составляется функция Лагранжа
при ограничениях, которые задаются экспертными суждениями. Решение задачи в произвольном случае предлагается выполнять методом множителей Лагранжа, когда составляется функция Лагранжа
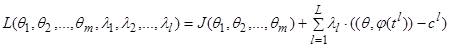 . (2)
. (2)
Частные производные по каждой переменной приравниваются к нулю, и решается система алгебраических уравнений. Отсюда находим вектор оценок параметров тренда.
В случае если функция 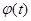 линейная или может быть сведена к линейной, в качестве меры близости рекомендуется функция
линейная или может быть сведена к линейной, в качестве меры близости рекомендуется функция
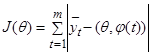 . (3)
. (3)
В этом случае задача сводится к задаче линейного программирования. Для этого вводятся вспомогательные переменные [2]:
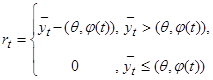 . (4)
. (4)
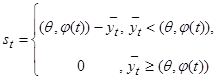 . (5)
. (5)
Очевидно, что
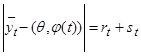 и
и 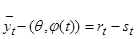 . (6)
. (6)
Рассмотрим на примере логистической кривой, которую иногда называют кривой Перла-Рида. Приведем уравнение кривой
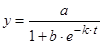 (7)
(7)
к линейному виду. Для этого прологарифмируем обе части равенства и используя свойства логарифма проведем равносильные преобразования. В результате получим уравнение вида:
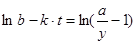 .
.
Введем обозначения:
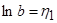 ,
, 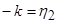 ,
, 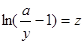 .
.
Тогда уравнение кривой может быть записано в виде:
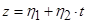 . (8)
. (8)
Для построения прогноза были подобраны 5 экспертов. Все они имеют высшее экономическое образование и являются специалистами с опытом работы в налоговой инспекции или государственных экономических структурах.
Кривая Гомперца и логистическая кривая при определенных значениях своих параметров имеют асимптоты. Эксперты оценивают нижнее предельное значение кривой Гомперца (параметр k в уравнении кривой) или верхнее предельное значение логистической кривой (т.е. параметр a в уравнении кривой), а затем каждый эксперт должен высказать свое суждение относительно поведения кривой. Например, «Значение временного ряда в момент времени t окажется не менее величины Аl, но не более величины Вl», где 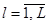 ,
, 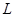 – число экспертов. При опросе каждый эксперт должен выразить свое суждение в виде одного из следующих утверждений [3]:
– число экспертов. При опросе каждый эксперт должен выразить свое суждение в виде одного из следующих утверждений [3]:
· Значение временного ряда будет в интервале от Аl до Вl;
· Значение временного ряда будет возрастать;
· Значение временного ряда будет убывать;
· Значение временного ряда будет больше значения Аl;
· Значение временного ряда будет меньше значения Вl;
· Значение временного ряда будет связано с одним из значений ряда в прошлом.
В данных постановках используется прогнозирование с учетом разнородной информации, т.е. используется временной ряд данных и информация экспертов. Покажем на примере логистической кривой, как для разных высказываний экспертов формируется задача линейного программирования.
В случае высказывания №1 мы получаем следующую систему:
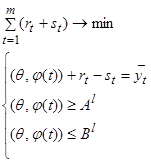 (9)
(9)
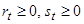 ,
, 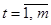 ,
, 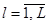 .
.
В случае высказывания №2 к системе ограничений добавляется условие 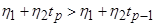 , где p период упреждения прогноза.
, где p период упреждения прогноза.
В случае высказывания №3 к системе ограничений добавляется условие 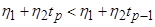 , где p период упреждения прогноза.
, где p период упреждения прогноза.
В случае высказывания №4 мы получаем следующую систему:
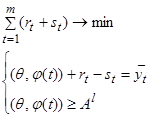 (10)
(10)
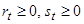 ,
, 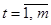 ,
, 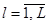 .
.
В случае высказывания №5 мы получаем следующую систему:
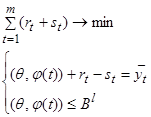 (11)
(11)
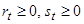 ,
, 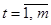 ,
, 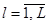 .
.
В случае высказывания №6 к системе ограничений добавляется условие 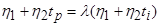 , где p – период упреждения прогноза, i – номер одного из значений временного ряда в прошлом, λ – некоторое число.
, где p – период упреждения прогноза, i – номер одного из значений временного ряда в прошлом, λ – некоторое число.
Описание используемого программного продукта
Обработка статистических данных на основе однородной информации производится с помощью Microsoft Excel. Для реализации предложенных моделей прогнозирования с использованием экспертных суждений нами используется программный продукт Maple, выпускаемый университетом Ватерлоо. Его называют системой символьных вычислений, или системой компьютерной алгебры. Он предназначен для выполнения самых разных математических вычислений, как аналитических, так и символьных. Его интерфейс интуитивно понятен, правила работы предельно просты, а возможности внушительны. В зависимости от выбранной модели аппроксимации тренда и вида экспертных суждений, формируется целевая функция и система ограничений. Для решения задач линейной оптимизации используется пакет «Simplex», а для нелинейной оптимизации – пакет «Optimization», в случае ограничений в форме равенств и неравенств [1].
Результаты прогнозирования показателей
В таблице 1 приведены временные ряды по выбранному показателю - платежам в консолидированный бюджет Забайкальского края [4,5].
Таблица 1
|
Год |
Величина налоговых поступлений, млн. руб. (до 1998г. в млрд.руб.) |
Год |
Величина налоговых поступлений, млн. руб. (до 1998г. в млрд.руб.) |
|
1991 |
1,8 |
2000 |
2418 |
|
1992 |
14,2 |
2001 |
4121,5 |
|
1993 |
142,8 |
2002 |
6132,3 |
|
1994 |
523,1 |
2003 |
9223 |
|
1995 |
983,6 |
2004 |
9826 |
|
1996 |
1439 |
2005 |
9784,6 |
|
1997 |
1663,8 |
2006 |
10496,3 |
|
1998 |
1378 |
2007 |
13265,5 |
|
1999 |
1670,1 |
2008 |
16314,6 |
Для прогнозирования показателей предлагается сглаживание и аппроксимация одним из типов функций [6]:
- Сглаживание
· Метод простой скользящей средней;
· Метод взвешенной скользящей средней;
· Экспоненциальное сглаживание.
- Аппроксимация функцией
· Полиномиальная (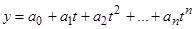 );
);
· Экспонента (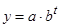 );
);
· Модифицированная экспонента (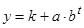 );
);
· Кривая Гомперца (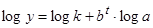 );
);
· Логистическая кривая (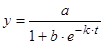 ).
).
Для аппроксимации данных логистической кривой предлагается оценивание параметров при помощи регрессии (метод Родса) [6], а для аппроксимации данных кривой Гомперца предлагается оценивание параметров на основе метода трех сумм [6].
Результаты экспериментов на примере выбранного показателя представлены в таблице 2. Прогноз по наиболее «удачной» модели выделен жирным шрифтом.
Таблица 2
|
№ |
Название метода |
Прогноз на 2008г. по данным 1991-2007гг. |
|
|
Точность 5% будет соблюдена, если прогнозируемое значение попадет в интервал |
15498,9 - 17130,3 |
|
1 |
Простая скользящая средняя |
13358,8 |
|
2 |
Взвешенная скользящая средняя |
12158,9 |
|
3 |
Экспоненциальное сглаживание |
12981,4 |
|
4 |
Полиномиальная функция, N=2 |
15220,8 |
|
5 |
Полиномиальная функция, N=3 |
15050,0 |
|
6 |
Экспонента |
25164,2 |
|
7 |
Модифицированная экспонента |
21345,1 |
|
8 |
Кривая Гомперца (метод трех сумм) |
16171,8 |
|
9 |
Кривая Гомперца (с использованием экспертных оценок) |
17612,6 |
|
10 |
Логистическая кривая (метод Родса) |
11329,6 |
|
11 |
Логистическая кривая (с использованием экспертных оценок) |
15153,2 |
По налоговым поступлениям наилучшее прогнозное значение дает кривая Гомперца. Для прогнозирования выбранного показателя на 2008г. целесообразно использовать полиномиальную функцию, а также кривую Гомперца и логистическую кривую с учетом экспертных суждений.
Выводы
1. Предложенный подход к прогнозированию налоговых платежей на основе статистических данных и суждений квалифицированных в предметной области экспертов способствует получению более достоверных результатов прогноза развития налоговой системы, что позволит органам управления налоговой службы получать научно-обоснованные прогнозные показатели налоговых поступлений в плановом периоде, а местным органам управления определять потенциал региона для решения социально-экономических задач.
2. Данный подход, примененный к налоговым поступлениям, можно использовать и для прогнозирования других показателей.
3. Отследив общую тенденцию динамики налоговых поступлений в дальнейшем можно составлять прогнозы отдельно для каждого муниципального образования Забайкальского края.
Литература
1. Говорухин В. Компьютер в математическом исследовании/ В. Говорухин, Б. Цибулин – М.:Мир, 2006. -619с.
2. Головченко В.Б. Прогнозирование с использованием разнородной информации/ В.Б. Головченко. - Иркутск: Изд-во БГУЭП, 2005. – 71с.
3. Краковский Ю.М. Прогнозирование динамики развития рынка образовательных услуг на примере специальности «Экономика предприятия»/ Ю.М. Краковский, А.С. Яхина// Вестник развития науки и образования. – М.: Наука, 2009. №1 – с.46-52.
4. Статистический ежегодник. г. Чита, 2008.
5. Статистический отчет «Форма 1-НМ» «О начислении и поступлении налогов, сборов и иных обязательных платежей в бюджетную систему РФ по Забайкальскому краю (сводная таблица)».-2008.
6. Четыркин Е.М. Статистические методы прогнозирования/ Е.М. Четыркин - М.: Статистика, 1975. – 184с.







