В представленной работе проведено моделирование в среде MATLAB/Simulink, в результате которого получены параметры ориентации и навигации. Проведен сравнительный анализ с данными встроенного вычислителя БИНС.
Ключевой проблемой обеспечения безопасности на железных дорогах остается контроль состояния рельсового пути. В России, а особенно в азиатской ее части, существуют дефицит железнодорожных путей, которые вносят огромный вклад в экономическое, демографическое и культурное развитее региона. От состояния рельсового пути зависит безопасность и скорость при перевозке людей и доставке товаров. В настоящие время контроль рельсового пути проводиться с помощью путеизмерительных вагонов и ручных путеизмерительных тележек. Для определения геометрических параметров рельсовых нитей таких, как уровень, продольный уклон, кривизна, отклонения от прямолинейного положения в плане прямых участков пути, горизонтальные и вертикальные ускорения кузова, в ПВ используется информация от БИНС.
1. Разработка модели в среде Matlab/Simulink.
Моделирование служит для наблюдения, предсказания поведения объекта и выбора свойств объекта (критерия эффективности работы), оптимизации работы при задании тех или иных входных условий, воздействий. Применительно к БИНС можно выделить такие задачи моделирования как исследование математической модели БИНС в реальном времени и определение точности выработки параметров с учетом погрешностей ЧЭ, входящих в БИНС, и внешних возмущений. Следовательно, составление достоверной модели является ключевым моментом.
Для моделирования алгоритма БИНС была выбрана среда Matlab/Simulink. Эта программа позволяет применять различные походы к моделированию, имеет расширенный набор функций, блоков и пакетов для аппроксимации, статистической обработки данных, решения дифференциальных уравнений, позволяет проводить дифференциальные и интегральные исчисления. Пакет Simulink расширяет возможности для моделирования, имитации поведения сложных систем и разработки новых систем и подсистем.
В соответствии со структурной схемой БИНС построим модель в среде Matlab/Simulink. При моделирование не рассматривался вертикальный канал, поэтому исключается блок выработки вертикальной скорости, и проекций высоты.
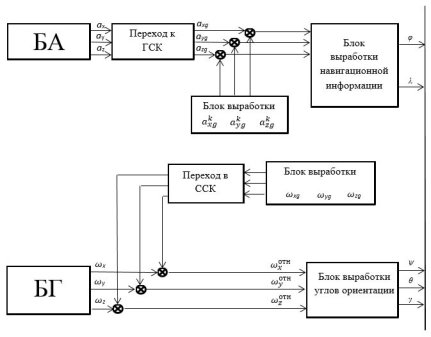
Рис. 1. Блок-схема работы алгоритма БИНС
Блок акселерометров (БА) вырабатывает проекции вектора кажущегося ускорения nx, ny, nz на оси ССК. Далее с помощью матрицы С производится пересчет nx, ny, nz из ССК в ГСК (блок «Переход к ГСК»). Матрица С формируется по данным от ДУС согласно выражению. В результате образуются проекции кажущегося ускорения aXg, aYg и aZg.
В «Блоке выработки
Для определения координат местоположения объекта (широты и долготы) ускорения относительного движения поступают в «Блок выработки навигационной информации», где производится двукратное интегрирование о![]() ,
,![]() и
и ![]() при начальных условиях.
при начальных условиях.
В «Блоке выработки ![]() ,
, ![]() ,
, ![]() » формируются проекции вектора абсолютной угловой скорости географического трехгранника
» формируются проекции вектора абсолютной угловой скорости географического трехгранника ![]() ,
, ![]() ,
, ![]() . Затем полученные проекции с помощью матрицы А перепроектируются из ГСК в ССК, то есть формируются компоненты переносной угловой скорости
. Затем полученные проекции с помощью матрицы А перепроектируются из ГСК в ССК, то есть формируются компоненты переносной угловой скорости ![]() ,
, ![]() ,
,![]() (блок «Переход в ССК»). Затем эти составляющие поступают в часть схемы, отвечающей за алгоритм ориентации.
(блок «Переход в ССК»). Затем эти составляющие поступают в часть схемы, отвечающей за алгоритм ориентации.
Из показаний датчиков угловой скорости (БГ – блок гироскопов) исключаются компоненты ![]() ,
, ![]() ,
,![]() . Таким образом, будут получены относительные угловые скорости
. Таким образом, будут получены относительные угловые скорости ![]() ,
, ![]()
![]() , из которых образуются , θ и γ. Далее производится их интегрирование и на выход «Блока углов выработки ориентации» поступают данные о углах рыскания , тангажа θ и крена γ.
, из которых образуются , θ и γ. Далее производится их интегрирование и на выход «Блока углов выработки ориентации» поступают данные о углах рыскания , тангажа θ и крена γ.
Основные соотношения:
Проекции относительной угловой скорости
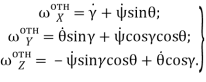
Кинематические уравнения в углах Эйлера-Крылова
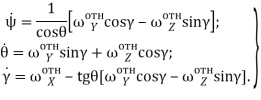
Углы поворотов Эйлера-Крылова
 ,
,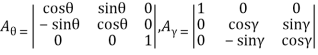
2. Результаты моделирования.
Рассмотренные данные были взяты с участка ж. д. «Вырица-Коммунар».
В результате моделирования БИНС с учетом начальных значений мы получили следующие результаты и сравнили их с вычислителем БИНС, на рисунках показаны результаты вычислителя и модели. Рассчитаем абсолютную погрешность для каждого графика.
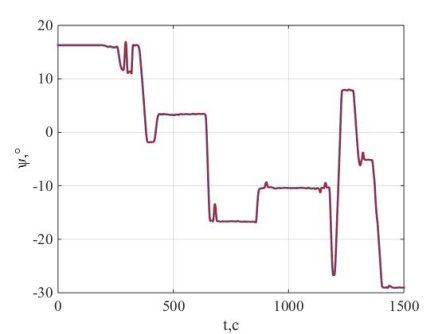
Рис. 2. Угол рысканья
Погрешность моделирования составила 0,36’. Описать увел рисунок. На увеличенном фрагменте графика представлено максимальное отклонение показаний модели от вычислителя.
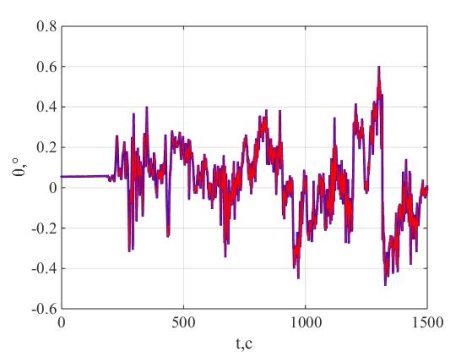
Рис. 3. Угол тангажа
Погрешность моделирования составила 0,72’
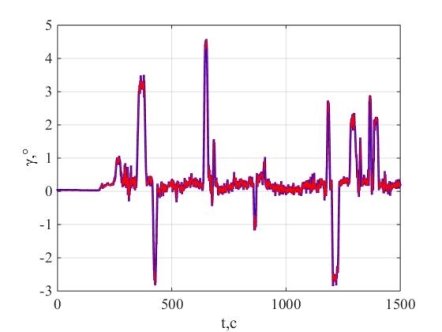
Рис. 4. Угол крена
Погрешность моделирования составила 4,32’
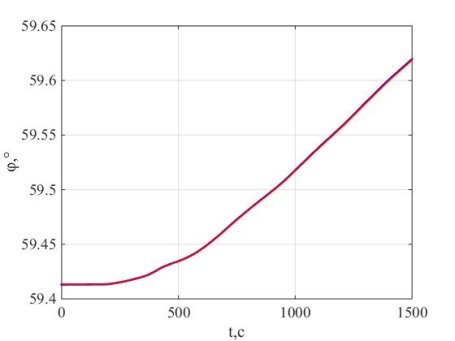
Рис. 5. Широта
Погрешность моделирования составила 2,16’
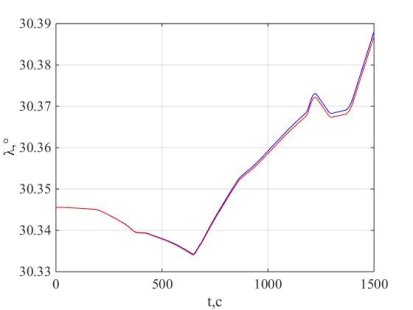
Рис. 6. Долгота
Погрешность моделирования составила 3,24’
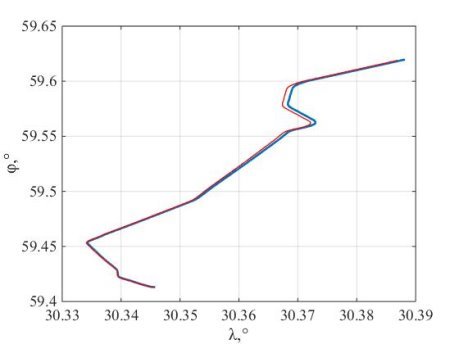
Рис. 7. Траектория движения объекта
Заключение.
В данной работе была разработана модель алгоритма БИНС в среде MATLAB/Simulink. Получены параметры ориентации (углы курса, тангажа и крена), навигации (долгота и широта), также представлена траектория движения объекта. Получены погрешности между нашей моделью и вычислителем, максимальная погрешность моделирования составила 4.32’ по параметрам ориентации и 3,24’ по параметрам навигации.
Литература:
- Боронахин А. М., Иванов П. А., Подгорная Л. Н., Ткаченко А. Н. Интегрированные инерциальные технологии динамического мониторинга рельсового пути. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2014. 170 с.
- Филипеня Н. С. Разработка инерциальных методов и средств измерения параметров рельсового пути /диссертация на соискание уч. ст. к. т. н. / СПб, 2007.







